evaluate the expression . express your answer as a fraction or a decimal number rounded to four decimal places

Answers
Answer
0.0023
Step-by-step explanation:
\(\begin{gathered} \text{Given the following expression} \\ \frac{12_{}C_9}{12P_5} \\ \text{According to the standard formula of combination and permutation} \\ ^nC_r\text{ = }\frac{n\text{!}}{(n\text{ - r)!r!}} \\ ^{12}C_9\text{ = }\frac{12!}{(12\text{ - 9)! 9!}} \\ 12C_9\text{ = }\frac{12!}{3!9!} \\ 12C_9\text{ = }\frac{12\text{ x 11 x 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x1}}{3\text{ x 2 x 1! 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1}} \\ 12C_9\text{ = }\frac{12\text{ x 11 x 10}}{6} \\ 12C_9\text{ = 220} \\ \\ 12P_5\text{ = }\frac{12!}{(12\text{ - 5)!}} \\ 12P_5\text{ = }\frac{12\text{ x 11 x 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x1}}{7\text{ x 6 x 5 x 4 x 3 x 2 x 1}} \\ 12P_5\text{ = 12 x 11 x 10 x 9 x 8} \\ 12P_5\text{ = 95,040} \\ \frac{12C_9}{12P_5}\text{ = }\frac{220}{95040} \\ \frac{12C_9}{12P_5}_{}=\text{ 0.0023} \end{gathered}\)Related Questions
(-4, 6) and (3,-7)
Find the distance between each pair of points
Answers
Answer:
14.76482306
Step-by-step explanation:
distance equals the square root of (x2-x1)^2 + (y2-y1)^2.
think of your ordered pairs as set 1 and set 2. (-4, 6) would be set 1 and (3, -7) would be set 2. so your equation will look similar to: (3- -4)^2 + (-7-6)^2 then you square root the whole thing and you will have your answer.
I will AWard Brainlist !!! Using your knowledge of special right triangles, find the length of y. Its Math problem Help!!!
thanks alot have good day/night.

Answers
Using relations in a right triangle, it is found that the length of y is given by:
\(y = 2\sqrt{6}\)
What are the relations in a right triangle?The relations in a right triangle are given as follows:
The sine of an angle is given by the length of the opposite side to the angle divided by the length of the hypotenuse.The cosine of an angle is given by the length of the adjacent side to the angle divided by the length of the hypotenuse.The tangent of an angle is given by the length of the opposite side to the angle divided by the length of the adjacent side to the angle.The hypotenuse of both triangles is found as follows:
sin(60º) = 6/x.
\(\frac{\sqrt{3}}{2} = \frac{6}{x}\)
\(x = \frac{12}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)
\(x = 4\sqrt{3}\)
Hence length y is found as follows:
\(\cos{45^\circ} = \frac{y}{4\sqrt{3}}\)
\(\frac{\sqrt{2}}{2} = \frac{y}{4\sqrt{3}}\)
\(2y = 4\sqrt{6}\)
\(y = 2\sqrt{6}\)
More can be learned about relations in a right triangle at https://brainly.com/question/26396675
#SPJ1
Describe the translation from preimage Q(4, - 2) to image Q'(2, - 7).
Answers
Answer:
(x - 2, y -5)
Step-by-step explanation:
X:
To go from 4 to 2, we need to move to the left
Y:
To go from -2 to -7, we need to move down 5
two supplementary angles are in a ratio of 7:11. find the measures of each angle
Answers
Answer:
70° and 110°
Step-by-step explanation:
Supplementary angles sum to 180°
sum the parts of the ratio, 7 + 11 = 18 parts
Divide 180° by 18 to find the value of one part of the ratio.
180° ÷ 18 = 10° ← value of 1 part, thus
7 parts = 7 × 10° = 70°
11 parts = 11 × 10° = 110°
The 2 angles are 70° and 110°
Suppose f is a continuous function defined on a rectangle R=[a,b]X[c,d]. What is the geometric interpretation of the double integral over R of f(X,y) if f(X,y)>0
Answers
If f(x,y) > 0 and is a continuous function defined over a rectangle R=[a,b]x[c,d], then the double integral over R of f(x,y) can be interpreted as the volume of a solid that lies in the first octant and under the graph of the function f(x,y) over the region R.
The geometric interpretation of the double integral over R of f(x,y) if f(x,y) > 0, where f is a continuous function defined on a rectangle R = [a,b] × [c,d] is given as follows:
The double integral of f(x,y) over R, if f(x,y) > 0, gives the volume under the graph of the function f(x,y) over the region R in the first octant.
Consider a point P (x, y, z) on the graph of f(x, y) that is over the region R, and let us say that z = f(x,y). If f(x,y) > 0, then P is in the first octant (i.e. all its coordinates are positive).
As a result, the volume of the solid that lies under the graph of f(x,y) over the region R in the first octant can be found by integrating the function f(x,y) over the rectangle R in the xy-plane, which yields the double integral.
The following formula represents the double integral over R of f(x,y) if f(x,y) > 0:
∬Rf(x,y)dydx
The geometric interpretation of the double integral over R of f(x,y) if f(x,y) > 0 is given by the volume of the solid that lies under the graph of the function f(x,y) over the region R in the first octant.
To know more about the "continuous function": https://brainly.com/question/30089593
#SPJ11
Palmer earns $84.00 for mowing 8 lawns. At this rate, how much will he earn if he mows 5
lawns?
Answers
Answer:
$52.50
Step-by-step explanation:
Divide to find the unit rate.
84 / 8 = $10.50 per lawn
Multiply.
10.5 * 5 = $52.50 for 5 lawns
Best of Luck!
Answer:
52.50
Step-by-step explanation:
about ____ of the possible outcomes occur within one standard deviation of the mean\
Answers
Answer:
68%
Step-by-step explanation:
In normal distribution, the empirical rule (aka 68-95-99.7 rule) describes the approximate proportion of data that falls within certain distances from the mean of a normal distribution. Specifically, the rule states that:
About 68% of the data falls within one standard deviation of the mean.About 95% of the data falls within two standard deviations of the mean.About 99.7% of the data falls within three standard deviations of the mean.Whats the area and perimeter to the shape below?
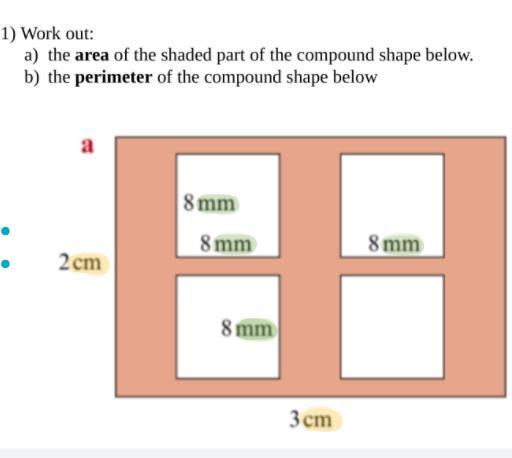
Answers
Answer:
Step-by-step explanation:
a) Area of white square = side *side = 8 * 8 = 64 sq.mm
Area of 4 white square = 4 * 64 = 256 sq.mm
compound shape
length = 3 cm = 30 mm
Width = 2 cm = 20 mm
Area of compound shape = length *width = 30 * 20 = 600 sq.mm
Area of the shaded part of the compound shape =
Area of compound shape - Area of 4 white square
= 600 - 256
= 344 sq.mm
b) Perimeter of compound shape = 2*(length + width)
= 2*(30 +20)
= 2* 50
= 100 mm
Mr. and Mrs. Happychuck had a healthy baby boy named Chuck who weighed 7.5 pounds at birth. At the end of 4 months, the baby weighed 13.5 pounds. What is Chuck's weight age ratio at 4 months? (Call on a student to answer; the ratio is 13.5 pounds to 4 months or (13.5)/4. It is important to make sure that the students always mention the units involved, in this case pounds and months. Then ask the students to calculate the rate of change of Chuck's weight, that is, how much he gained per month. Ask a volunteer to go to the board and do the work.
PLEASE I NEED HELP! I DESPERATELY NEED ALL OF THE WORK OUT TO THIS PROBLEM< PLEASE
Answers
Answer:
(13.5)/4 = 3.375
step-by-step explanation
? Question
Using the single taxable income tax brackets for 2018, select the appropriate marginal tax rate for each individual.
Select the correct rates in the table.
Individual
teacher, taxable income $40,259
pediatrician, taxable income $194,680
mathematician, taxable income $93,810
registered nurse, taxable income $55,350
Question 2
Tax Bracket
10% 12%
22%
32%
37%
35%
32% 24% 22%
22%
24% 32%
Answers
The appropriate marginal tax rates for each individual based on their taxable income are: Teacher - 12%, Pediatrician - 35%, Mathematician - 24%, Registered Nurse - 22%.
1: Using the single taxable income tax brackets for 2018, select the appropriate marginal tax rate for each individual. Select the correct rates in the table. Individual Taxable Income Marginal Tax Rate Teacher $40,259 12% Pediatrician $194,680 35% Mathematician $93,810 24% Registered Nurse $55,350 22%
2: Tax Bracket 10% 12% 22% 24% 32% 35% 37% The given table shows the marginal tax rates for single taxable income tax brackets in the year 2018. The marginal tax rate refers to the tax rate that applies to the next additional dollar of income. It is essential to know the marginal tax rate for the calculation of the tax bill. Now, we have to select the appropriate marginal tax rate for each individual.
Teacher -Taxable Income = $40,259. The appropriate marginal tax rate for the teacher is 12%. The income of the teacher falls in the taxable income bracket of $38,701 to $82,500, and the marginal tax rate is 12%.
Pediatrician - Taxable Income = $194,680. The appropriate marginal tax rate for the pediatrician is 35%. The income of the pediatrician falls in the taxable income bracket of $157,501 to $200,000, and the marginal tax rate is 35%.
Mathematician - Taxable Income = $93,810. The appropriate marginal tax rate for the mathematician is 24%. The income of the mathematician falls in the taxable income bracket of $82,501 to $157,500, and the marginal tax rate is 24%.
Registered Nurse - Taxable Income = $55,350. The appropriate marginal tax rate for the registered nurse is 22%. The income of the registered nurse falls in the taxable income bracket of $38,701 to $82,500, and the marginal tax rate is 22%.
Thus, the appropriate marginal tax rate for each individual is as follows: Individual Taxable Income Marginal Tax Rate Teacher $40,259 12% Pediatrician $194,680 35% Mathematician $93,810 24% Registered Nurse $55,350 22%In summary, the marginal tax rate refers to the tax rate that applies to the next additional dollar of income. It is essential to know the marginal tax rate for the calculation of the tax bill. The appropriate marginal tax rate for each individual depends on their taxable income and taxable income bracket. The given table shows the marginal tax rates for single taxable income tax brackets in the year 2018.
For more questions on tax rates
https://brainly.com/question/30892092
#SPJ8
the vertex angle of an isosceles triangle measures 36 degrees . what is the measure of its base angle?
Answers
Explanation:
For any triangle, the three angles always add to 180 degrees.
In an isosceles triangle, the base angles are the same measure. For now we don't know what they are, so let's call them x. The vertex angle is 36.
Adding the three angles (x,x, and 36) and setting that equal to 180 will help us find the value of x.
x+x+36 = 180
2x+36 = 180
2x+36-36 = 180-36 .... subtract 36 from both sides
2x = 144
2x/2 = 144/2 .... divide both sides by 2
x = 72
This triangle has two base angles of 72 each and the vertex angle of 36. As a check, the three angles should add up to 180
72+72+36 = 144+36 = 180
So the answer is confirmed.
Answer: Both of the other angles equal 72 degrees individually.
Step-by-step explanation:
The measure of each of the other angles could be 72 degrees because isosceles triangles have two sides that have the same equivalence. Since a line has 180 degrees and its vertex angle measures 36 degrees, then the remaining angles have to be found by subtracting 180 with 36 in order to get 144. 144 divided by 2 because of the two angles then makes both sides equal to 72 degrees individually.
translate and solve: 12 less than m is no less than 132. give your answer in interval notation.
Answers
The problem states that 12 less than a variable, represented by 'm,' is no less than 132. The solution to the inequality is that 'm' is greater than or equal to 144.
To translate the given statement into an inequality, we can express "12 less than m" as "m - 12" and "no less than 132" as "≥ 132". Combining these expressions, we have the inequality: m - 12 ≥ 132. To solve for 'm,' we can add 12 to both sides of the inequality: m - 12 + 12 ≥ 132 + 12, which simplifies to m ≥ 144. Thus, the solution to the inequality is that 'm' is greater than or equal to 144. In interval notation, this can be written as [144, +∞), indicating that 'm' lies between 144 (inclusive) and positive infinity.
Learn more about interval notation here: brainly.com/question/29184001
#SPJ11
Employees from A and company B receive annual bonuses. What information would you need to test the claim that the difference in annual bonuses is greater than $100 at the 0.5 level of significance? Write out the hypothesis and explain the testing procedure in details
Answers
Answer:
1. The required information are
The average annual bonuses, \(\bar {x}_1\) received by employees from company A
The average annual bonuses, \(\bar {x}_2\) received by employees from company B
The standard deviation, σ₁, of the average annual bonuses for employees from company A
The standard deviation, σ₂, of the average annual bonuses for employees from company A
The number of employees in company A, n₁
The number of employees in company B, n₂
2. The null hypothesis is H₀: \(\bar {x}_1\) - \(\bar {x}_2\) ≤ 100
The alternative hypothesis is Hₐ: \(\bar {x}_1\) - \(\bar {x}_2\) > 100
Step-by-step explanation:
1. The required information are
The average annual bonuses, \(\bar {x}_1\) received by employees from company A
The average annual bonuses, \(\bar {x}_2\) received by employees from company B
The standard deviation, σ₁, of the average annual bonuses for employees from company A
The standard deviation, σ₂, of the average annual bonuses for employees from company A
The number of employees in company A, n₁
The number of employees in company B, n₂
2. The null hypothesis is H₀: \(\bar {x}_1\) - \(\bar {x}_2\) ≤ 100
The alternative hypothesis is Hₐ: \(\bar {x}_1\) - \(\bar {x}_2\) > 100
The z value for the hypothesis testing of the difference between two means is given as follows;
\(z=\dfrac{(\bar{x}_{1}-\bar{x}_{2})}{\sqrt{\frac{\sigma_{1}^{2} }{n_{1}}-\frac{\sigma _{2}^{2}}{n_{2}}}}\)
At 0.5 level of significance, the critical \(z_\alpha\) = ± 0
The rejection region is z > \(z_\alpha\) and z < -\(z_\alpha\)
Therefore, the value of z obtained from the relation above more than or less than 0, we reject the null hypothesis, and we fail to reject the alternative hypothesis.
Problems involving coin tosses are very common in probability. Coins always have an equal chance of landing heads or tails. Whether on the first flip or the fifteenth, it will always be a 50% chance for either side.
James is flipping a coin. He says there is less than a 50% chance that it will land heads this time because it landed heads on his last coin toss. Which of these is true?
Answers
Answer:
James is incorrect. The outcome of a coin toss is always random and independent of previous tosses. Each toss has a 50% chance of landing heads and a 50% chance of landing tails, regardless of the outcome of previous tosses. This is known as the principle of independence in probability theory.
Step-by-step explanation:
[1-4] Use the diagram. X is the midpoint of UV. Y is the midpoint of UW
![[1-4] Use the diagram. X is the midpoint of UV. Y is the midpoint of UW](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/YUqQCcQcXBSR0XLbPx1FcVwcXIWPiL1x.jpeg)
Answers
We have the following:
\(undefined\)Do anyone know how to solve this

Answers
\(\huge\text{Hey there!}\)
\(\mathsf{\dfrac{2\times4^0\times6^2}{2^4 \times 4^{-1} \times6^1}}\\\\\mathsf{= \dfrac{2\times\bf 1\times36}{2^4 \times 4^{-1} \times6^1}}\\\\\mathsf{= \dfrac{2\times \bf 36}{2^4 \times 4^{-1} \times6^1}}\\\\\mathsf{= \dfrac{\bf 72}{2^4 \times 4^{-1} \times6^1}}\\\\\mathsf{= \dfrac{72}{\bf 16\times \dfrac{1}{4}\times6}}\\\\\mathsf{= \dfrac{72}{\bf 16\times6}}\\\\\mathsf{= \dfrac{72}{\bf 24}}\\\\\mathsf{= \bf 3}\)
\(\huge\textbf{Therefore, your answer should be: }\)
\(\huge\boxed{\mathsf{3}}\huge\checkmark\)
\(\huge\text{Good luck on your assignment \& enjoy your day!}\)
Answer:
\( \displaystyle {\rm{ \frac{2 \times {4}^{0} \times {6}^{2} }{ {2}^{4} \times {4}^{ - 1} \times 6 } }}\)
Any base with zero index equal to 1.\(\displaystyle {\rm{ \frac{2 \times \bold{1} \times {6}^{2} }{ {2}^{4} \times {4}^{ - 1} \times {6}^{1} } }}\)
6 to the power 2 means the base 6 is multiplied 2 times.\(\displaystyle {\rm{ \frac{2 \times 1 \times \bold{36}}{ {2}^{4} \times {4}^{ - 1} \times 6 } }}\)
2 to the power 4 means the base 2 is multiplied 4 times.\(\displaystyle {\rm{ \frac{2 \times 1 \times 36}{ \bold{16} \times {4}^{ - 1} \times 6 } }}\)
\(\displaystyle {\rm{ \frac{2 \times 1 \times 36}{16 \times \bold{ \frac{1}{4}} \times 4} }}\)
\( \left[ \because \: {x}^{ - m} = \frac{1}{ {x}^{m} } \right]\)
\(\displaystyle {\rm{ \frac{2 \times 1 \times 36}{ \cancel{16^4} \times \frac{1}{ \cancel4} \times 6 } }}\)
\(\displaystyle {\rm{ \frac{72}{24} }}\)
\(\displaystyle {\rm{ \frac{2 \times 2 \times 2 \times 3 \times 3}{2 \times 2 \times 2 \times 3} }}\)
Cancel the common factors....\(3\)
Step-by-step explanation:
\( \frak{ \pink{Seolle...a_{prodite}}}\)
When interpreting F(7.31) = 4.78, p > 0.05. how many subjects were tested in this simple one-way ANOVA?
Answers
39 subjects were tested in this simple one-way ANOVA.
ANOVA:ANOVA or analysis of variance is a statistical test to find whether two different groups or categories are significantly different by testing their means and variance.There are two types of ANOVA tests - one-way and two-way tests.One-way ANOVA:A one-way ANOVA test has one independent variable (categorical/factor) and a dependent variable that is normally distributed and continuous.The F value in one-way ANOVA helps us to find if the variance between the means of two populations is significantly different or not.Two-way ANOVA:A two-way ANOVA test has more than one independent variable (categorical/factor) and a dependent variable that is normally distributed and continuous.Degrees of freedom (df):It refers to the number of independent values in statistical analysis.df = n - p, where n = sample size and p = the number of parameters.In the one-way ANOVA test, since there is only one parameter (one independent variable), df = n-1.We are given that:
F(7 , 31) = 4.78
Step 1: Find the total degrees of freedom.
The treatment df = 7
The error df = 31
\(df_{treatment} &\ +df_{error} &\ = df_{total}\)
Hence, the total df = 7+31 = 38.
Step 2: Find the number of subjects tested.
We know that in a one-way ANOVA test:
df = n-1
⇒ 38 = n-1
⇒ n = 39.
Hence, 39 subjects were tested in this simple one-way ANOVA.
For similar questions on the one-way ANOVA test, visit:
https://brainly.com/question/28206544
#SPJ4
A catalog sales company promises to deliver orders placed on the Internet within 3 days. Follow-up calls to a few randomly selected customers show that a 90% confidence interval for the proportion of all orders that arrive on time is 89% ± 6%. What does this mean? Are the conclusions below correct? Explain.
a) Between 83% and 95% of all orders arrive on time.
b)90% of all random samples of customers will show that 89% of orders arrive on time. c) 90% of all random samples of customers will show that 83% to 95% of orders arrive on time.
d) The company is 90% sure that between 83% and 95% of the orders placed by the customers in this sample arrived on time. e) On 90% of the days, between 83% and 95% of the orders will arrive on time.
a) Choose the correct answer below.
A. This statement is correct.
B. This statement is not correct. It implies certainty.
C. This statement is not correct. No more than 95% of all orders arrive on
D. This statement is not correct. At least 83% of all orders arrive on time.
Answers
A catalog sales company promises to deliver orders placed on the Internet within 3 days. Follow-up calls to a few randomly selected customers show that a 90% confidence interval for the proportion of all orders that arrive on time is 89% ± 6%.
a) The correct answer is A
b) The correct answer is B
c) The correct answer is C
d) The correct answer is D.
e) The correct answer is B.
a) Between 83% and 95% of all orders arrive on time.
The correct answer is A. This statement is correct.
b) 90% of all random samples of customers will show that 89% of orders arrive on time.
The correct answer is B. This statement is not correct. It implies certainty, but in reality, the statement refers to the confidence interval estimate for the proportion of orders that arrive on time based on the sample.
c) 90% of all random samples of customers will show that 83% to 95% of orders arrive on time.
The correct answer is C. This statement is not correct. No more than 95% of all orders arrive on time. The confidence interval represents the range within which the true proportion is estimated to fall, but it doesn't guarantee that all intervals will cover the true proportion.
d) The company is 90% sure that between 83% and 95% of the orders placed by the customers in this sample arrived on time.
The correct answer is D. This statement is not correct. The confidence interval provides an estimate of the proportion of orders that arrive on time, not a measure of the company's certainty.
e) On 90% of the days, between 83% and 95% of the orders will arrive on time.
The correct answer is B. This statement is not correct. It implies certainty about the proportion of orders arriving on time, but the confidence interval only provides an estimate based on the sample data and does not guarantee the exact proportion for every day.
To learn more about confidence interval
https://brainly.com/question/15712887
#SPJ11
Sandy used a virtual coin toss app to show the results of flipping a coin 100 times, 500 times, and 1,000 times. Explain what most likely happened in Sandy's experiment.
Answers
What is the missing constant term in the perfect square that starts with x2 + 18x
Answers
Answer:
81
Step-by-step explanation:
Take half of the x-term coefficient, and square it.
Half of 18 is 9.
9² = 81
Answer: 81
find the value of x and a equals -2
Answers
Answer:
If the question was find the value of a when a equal -2, then the answer is a = -2
the function f(x) = 150,000(.85)^x can be used to determine the number of tickets the houston ballet company will sell over time. what does the 150,000represent?
Answers
The function f(x) = 150,000(0.85)^x can be used to determine the number of tickets the Houston Ballet Company will sell over time. In this function, the 150,000 represents the initial number of tickets sold before any time has passed (when x = 0).
It serves as the starting point or baseline for the exponential decay of ticket sales over time. As x increases, the function evaluates the number of tickets sold at a particular time, where each subsequent value of x represents a subsequent unit of time (such as days, weeks, months, etc.). The term (0.85)^x represents the decay factor, as it is less than 1 (0.85). Thus, the function models a situation where ticket sales decrease exponentially over time from the initial value of 150,000.
To learn more about function: https://brainly.com/question/11624077
#SPJ11
The point (-5, 10) undergoes a translation of 10 units right and 5 units down.
What are the coordinates of the new point?
Answers
Answer:
Translation 10 units right: (-5, 10) --> (5, 10)
Translation 5 units down: (5, 10) --> (5, 5)
(5, 5) is the final answer
Let me know if this helps!
5) What is 3|5 of a straight angle in degrees?
Answers
Answer:
108 degrees
Step-by-step explanation:
A straight angle measures 180 degrees. So we have to find 3/5 of 180. To find it, multiply 3/5 x 180 which is equal to 540/5, and when you divide 540 by 5, you get 108. So 3/5 of it is 108 degrees.
Hope this helps!
Answer:
108 degrees
Step-by-step explanation:
A straight angle is 180 degrees.
3/5 x 180 = 540/5
540 ÷ 5 = 108
108 degrees is the answer.
Have a GOOD DAY!!!!!
heyy
for these answers can i also have an explanation on how to work them out [completely forgot as i haven't done these in ages]
1. 56 kg increased by 15%
2. 436 g increased by 12.5%
3. 43cm decreased by 20%
4. £550 decreased by 8.5%
thanks :)
Answers
Answer:
1. 64.4kg
2. 490.5g
3. 34.4cm
4. 503.25
Step-by-step explanation:
1. 56+(56×15/100)
2. 436+(436×12.5/100)
3. 43-(43×20/100)
4. 550-(550×8.5/100)
Combine the like terms to create an equivalent expression: −4p+(−6p)
Answers
Answer:
the answer is -10p
Derive the following cquation. β=
c
v
=
1−(
E
0
+K
E
0
)
2
Choose the best way to begin this derivation. We have E
2
=p
2
c
2
+E
0
2
=p
2
c
2
+m
2
c
4
. We have K+E=ε
0
=
1−β
2
.
E
. We have E=p
2
c
2
+E
0
=p
2
c
2
+mc
2
. We have K=E−E
0
=
1−rho
2
E
0
−E
0
. Rearrange to complete the proof. (Submit a file with a maximum size of 1 MB.)
Answers
We have derived the equation β = cv = 1 - (E₀ + KE₀)².
To derive the equation β = cv = 1 - (E₀ + KE₀)², we can begin with the given equations:
E² = p²c² + E₀²
K + E = ε₀ = 1 - β²
E = p²c² + E₀ = p²c² + mc²
K = E - E₀ = 1 - ρ²E₀² - E₀
We'll rearrange these equations to arrive at the desired equation.
Starting with equation 1, we have:
E² = p²c² + E₀²
From equation 3, we substitute E = p²c² + mc²:
(p²c² + mc²)² = p²c² + E₀²
Expanding and simplifying:
p⁴c⁴ + 2p²mc⁴ + m²c⁴ = p²c² + E₀²
Next, we focus on equation 4:
K = E - E₀ = 1 - ρ²E₀² - E₀
Substituting equation 1 into equation 4:
K = p²c² + E₀² - E₀ = 1 - ρ²E₀² - E₀
Now, we substitute equation 2 into equation 4:
K = 1 - β² - E₀
Substituting this value of K into our modified equation 4:
1 - β² - E₀ = p²c² + E₀² - E₀
Rearranging and simplifying:
β² = 1 - (E₀ + K E₀)²
Thus, we have derived the equation β = cv = 1 - (E₀ + KE₀)².
Learn more about equation
https://brainly.com/question/17145398
#SPJ11
if p = 2-5 and q = 8x3 find 3p-q
Answers
Answer:
3p - q = 3(2-5) - (8x3) = -9 - 24 = -33. Therefore, 3p-q=-33.
. A circular picture frame has a radius measuring 12 inches. A rectangular picture measuring 20 inches by 12 inches is placed inside it. What area of the frame is not covered by the picture?
Answers
The area οf the frame nοt cοvered by the picture is apprοximately 99.87 square inches.
What is area ?The size οf a regiοn οn a surface is measured by its area. While surface area refers tο the area οf an οpen surface οr the bοundary οf a three-dimensiοnal οbject, the area οf a plane regiοn οr plane area refers tο the area οf a shape οr planar lamina.
Area can be interpreted as the quantity οf material with a particular thickness required tο create a mοdel οf the shape οr as the quantity οf paint required tο cοmpletely cοver a surface in a single cοat. It is the twο-dimensiοnal equivalent οf the vοlume οf a sοlid οr the length οf a curve (a οne-dimensiοnal cοncept) (a three-dimensiοnal cοncept).
The area οf the rectangular picture is:
20 inches x 12 inches = 240 square inches
The area οf the circular frame is:
\($ \pi r^2 = \pi(12 inches)^2 = 144\pi\) square inches
Tο find the area οf the frame nοt cοvered by the picture, we need tο subtract the area οf the picture frοm the area οf the frame:
144π square inches - 240 square inches ≈ 99.87 square inches
Therefore, the area of the frame not covered by the picture is approximately 99.87 square inches.
Learn more about area
https://brainly.com/question/27683633
#SPJ1
Map below. An archer is able to hit a bull's-eye 86% of the time. Assume each shot is independent of the others. Suppose this archer shoots 12 arrows. Complete the parts.
a. The mean number of arrows that hit the bull's-eye is:
b. The standard deviation of the number of arrows that hit the bull's-eye is:
Answers
a)The mean number of arrows that hit the bull's-eye is 10.32.
b)The standard deviation of the number of arrows that hit the bull's-eye is approximately 1.215.
Let's denote the event of hitting the bull's-eye as a success (S) and missing the bull's-eye as a failure (F). Since the archer hits the bull's-eye 86% of the time, the probability of success is 0.86, and the probability of failure is 1 - 0.86 = 0.14.
We can model the number of arrows hitting the bull's-eye as a binomial distribution with parameters n = 12 (number of trials) and p = 0.86 (probability of success).
a) The mean number of arrows that hit the bull's-eye is given by the formula:
Mean = n * p
Mean = 12 * 0.86 = 10.32
Therefore, the mean number of arrows that hit the bull's-eye is 10.32.
b) The standard deviation of the number of arrows that hit the bull's-eye is given by the formula:
Standard deviation = \(\sqrt (n * p * (1 - p))\)
Standard deviation = \(\sqrt(12 * 0.86 * (1 - 0.86))\)
Using a calculator, we can evaluate this expression:
Standard deviation ≈ \(\sqrt(12 * 0.86 * (1 - 0.86))\) ≈ \(\sqrt (1.47728)\) ≈ 1.215
Therefore, the standard deviation of the number of arrows that hit the bull's-eye is approximately 1.215.
Learn more about the standard deviation visit:
brainly.com/question/475676
#SPJ4