ements
(8.08)
mts
Calculate the average rate of change for the graphed sequence from n = 1 to n = 3. (2 points)
{(1, 2), (2, 4), (3, 8). (4. 16), (5, 32). (6,64) }
70 +
.
60
50+
40+
30+
20 +
10+

Answers
Answer:
123+
will you be home 122333456780
124267
173
97
Answer:
The average rate of change form n = 1 to n = 3 is 3.
Step-by-step explanation:
n = 1 (1, 2)
n = 3 (3,8)
Rate of change: \(\frac{f(b)-f(a)}{b-a}\)
\(\frac{f(b)-f(a)}{b-a}=\frac{8-2}{3-1} =\frac{6}{2} =3\)
There the average rate of change form n = 1 to n = 3 is 3.
Hope this helps!
Related Questions
Can someone put this into vertex form?
y=x2+24x-15
Answers
Answer:
The vertex form of y = x² + 24x - 15 is y = (x + 12)² - 159
Step-by-step explanation:
The vertex form of the quadratic equation y = ax² + bx + c is
y = a(x - h)² + k, where
a is the coefficient of x²(h, k) are the coordinates of the vertex pointh = \(\frac{-b}{2a}\) , where b is the coefficient of xk = y at x = hLet us use the facts above to solve the question
∵ y = x² + 24x - 15
∵ a is the coefficient of x² and b is the coefficient of x
∴ a = 1 and b = 24
∵ h is the x-coordinate of the vertex point
∵ h = \(\frac{-b}{2a}\)
→ Substitute the values of a and b to find h
∴ h = \(\frac{-24}{2(1)}=\frac{-24}{2}\)
∴ h = -12
→ To find k substitute y by k and x by h
∵ y = k and x = h
∴ k = (-12)² + 24(-12) - 15 = 144 - 288 - 15
∴ k = -159
∴ The coordinates of the vertex point are (-12, -159)
→ Substitute the values of a, h, and k in the vertex form above
∵ y = 1(x - -12)² + (-159)
→ Remember (-)(-) = (+) and (+)(-) = (-)
∴ y = (x + 12)² - 159
∴ The vertex form of y = x² + 24x - 15 is y = (x + 12)² - 159
Answer:
sure.
Step-by-step explanation:
Shane, Cheryl, and Isaac went to the store to buy school supplies. Shane bought 4 pens, 3 folders, and 2 notebooks for a total of $12.25. Cheryl bought 4 folders and 6 notebooks for a total of $22. Isaiah bought 2 pens, 1 folder, and 3 notebooks for a total of $10.25. How much does each supply cost? Each pen costs $(1.25 0.50 0.75 1.75). Each folder costs $(2.75 1.75 2.50 1.25). Each notebook costs $(2.75 1.75 2.50 1.25).
Answers
The cost of each entity: each pen is $\(1.75\), each folder is $\(2.50\), and each notebook is $\(1.75\).
Let's assign variables to the costs of each supply:
Let the cost of each pen be P dollars.
Let the cost of each folder be F dollars.
Let the cost of each notebook be N dollars.
According to the given information, we can form the following equations:
For Shane:
\(4P + 3F + 2N = 12.25 (Equation \ 1)\)
For Cheryl:
\(4F + 6N = 22 (Equation \ 2)\)
For Isaiah:
\(2P + F + 3N = 10.25 (Equation \ 3)\)
To solve this system of equations, we can use substitution or elimination method.
Using the elimination method, let's multiply Equation 2 by 2 and Equation 3 by 4 to eliminate F:
\(8F + 12N = 44 (Equation \ 4)\\8P + 2F + 12N = 41 (Equation \ 5)\)
Now, subtract Equation 4 from Equation 5 to eliminate F:
\(8P + 2F + 12N - (8F + 12N) = 41 - 44\\8P - 6F = -3\)
Simplifying further, we have:
\(8P - 6F = -3 (Equation \ 6)\)
Now, let's multiply Equation 1 by 4 and Equation 3 by 3 to eliminate N:
\(16P + 12F + 8N = 49 (Equation \ 7)\\6P + 3F + 9N = 30 (Equation \ 8)\)
Now, subtract Equation 8 from Equation 7 to eliminate N:
\(16P + 12F + 8N - (6P + 3F + 9N) = 49 - 30\\10P + 9F - N = 19\)
Simplifying further, we have:
\(10P + 9F - N = 19 (Equation \ 9)\)
Now we have a system of equations consisting of Equation 6, Equation 9, and Equation 2:
\(8P - 6F = -3 (Equation \ 6)\\10P + 9F - N = 19 (Equation \ 9)\\4F + 6N = 22 (Equation \ 2)\)
To find the values of P, F, and N, we can solve this system of equations using any suitable method, such as substitution or elimination.
For more such questions on cost of each entity:
https://brainly.com/question/22097711
#SPJ8
If cosA = 24/25 tanB = 4/3 and angles A and B are in Quadrant I, find the value of tan(A−B).
Answers
If cosA = 24/25 tanB = 4/3 and angles A and B are in Quadrant I. The value of tan(A-B) is -23/33.
What is the value of tan(A-B)?We can start by using the identity: tan(A - B) = (tan A - tan B)/(1 + tan A tan B)
From the given information, we have:
cos A = 24/25, which means sin A = sqrt(1 - cos^2 A) = 7/25 (since A is in Quadrant I)
tan B = 4/3, which means sin B = 4/sqrt(4^2 + 3^2) = 4/5 and cos B = 3/sqrt(4^2 + 3^2) = 3/5
Now, we can use the definitions of sine and cosine to find tan A:
tan A = sin A / cos A = (7/25)/(24/25) = 7/24
Substituting the values we have found into the formula for tan(A - B), we get:
tan(A - B) = (tan A - tan B)/(1 + tan A tan B)
= [(7/24) - (4/3)]/[1 + (7/24)(4/3)]
= (-13/72)/(25/72)
= -13/25
Therefore, tan(A - B) = -13/25.
Learn more about tan(A - B) here:https://brainly.com/question/24305408
#SPJ1
I really stuck on this question can someone help me out? What rational number, when multiplied by an irrational number, has a product that is a rational number? a. 1/2 b. 1 c. 1/10 d. 0
Answers
Answer:
d. 0
Step-by-step explanation:
Given that:
A rational number is multiplied by a irrational number.
And the result is a rational number.
To find:
Such rational number wil be:
a. \(\frac{1}2\)
b. 1
c. \(\frac{1}{10 }\)
d. 0
Solution:
Let us consider the given options one by one.
Let the irrational number be = \(\pi\)
Checking option a.
Multiply \(\pi\) and \(\frac{1}2\).
Result is: \(\frac{\pi}2\) which is again irrational.
So, a. is not correct.
Checking option b.
Multiply \(\pi\) and 1.
Result is: \(\pi\) which is again irrational.
So, b. is not correct.
Checking option a.
Multiply \(\pi\) and \(\frac{1}{10}\).
Result is: \(\frac{\pi}{10}\) which is again irrational.
So, c. is not correct.
Checking option d.
Multiply \(\pi\) and 0.
Result is: 0 which is rational.
So, d. 0 is the correct answer.
Please help me need help me please please help me

Answers
9514 1404 393
Answer:
(3) y = (x -3)²
Step-by-step explanation:
Try the first value of x in each function:
(1) y = 3² -3 ≠ 0
(2) y = (3 +3)² ≠ 0
(3) y = (3 -3)² = 0 . . . . . . matches the table value for f(3)
(4) y = 3² +3 ≠ 0
__
The only viable choice is (3).
suppose an atomic reactor has two independent cooling systems. the probability that cooling system a will fail is 0.02 and the probability that cooling system b will fail is 0.03 . what is the probability that both systems will fail simultaneously? round your answer to four decimal places, if necessary.
Answers
0.0006 .
The probability that both systems of an atomic reactor will fail simultaneously is 0.0006.
This is calculated by multiplying the probability of cooling system A failing (0.02) by the probability of cooling system B failing (0.03) which results in 0.0006, rounded to four decimal places.
Learn more about probability
brainly.com/question/16484393
#SPJ11
Gru's schemes have a/an 7% chance of succeeding. An agent of the Anti-Villain League obtains access to a simple random sample of 1100 of Gru's upcoming schemes. Find the probability that:
a. less than 101 schemes will succeed: _________
b. more than 95 schemes will succeed: ________
c. between 95 and 101 schemes will succeed: __________
Answers
Based on Gru's schemes the probability that a. less than 101 schemes will succeed: 0.9983; b. more than 95 schemes will succeed: 0.0018; c. between 95 and 101 schemes will succeed: 0.9966.
Gru's schemes have a 7% chance of succeeding. Total number of Gru's schemes = 1100.
Using binomial distribution, we can find out the probability of number of successes in n number of trials.
Probability of success in each trial p = 0.07
Probability of failure in each trial q = 1 - 0.07 = 0.93
a) Probability that less than 101 schemes will succeed.
Total number of trials n = 1100
P(X < 101) = P(X ≤ 100)
P(X ≤ 100) = ∑P(X = x) for x = 0, 1, 2, ..., 100
Now we can use normal distribution to approximate this probability as the sample size is large enough to apply central limit theorem. So,
mean (μ) = np = 1100 × 0.07 = 77
standard deviation (σ) = √[npq] = √[1100 × 0.07 × 0.93] = 7.233
Using standard normal distribution,
Z = (X - μ) / σ
Z = (100 + 0.5 - 77) / 7.233 = 2.99
So, P(X ≤ 100) = P(Z ≤ 2.99)
From standard normal distribution table,
P(Z ≤ 2.99) = 0.9983
Therefore, P(X < 101) = P(X ≤ 100) = 0.9983
b) Probability that more than 95 schemes will succeed.
P(X > 95) = P(X ≥ 96)
P(X ≥ 96) = ∑P(X = x) for x = 96, 97, ..., 1100
Now we can use normal distribution to approximate this probability as the sample size is large enough to apply central limit theorem. So,
mean (μ) = np = 1100 × 0.07 = 77
standard deviation (σ) = √[npq] = √[1100 × 0.07 × 0.93] = 7.233
Using standard normal distribution,
Z = (X - μ) / σ
Z = (96 - 0.5 - 77) / 7.233 = 2.91
So,
P(X ≥ 96) = P(Z ≥ 2.91)
From standard normal distribution table,
P(Z ≥ 2.91) = 0.0018
Therefore, P(X > 95) = P(X ≥ 96) = 0.0018
c) Probability that between 95 and 101 schemes will succeed.
P(95 ≤ X ≤ 101) = P(X ≤ 101) - P(X < 95)
P(X < 95) is already calculated in (a).
P(X ≤ 101) = 0.9983
Therefore,
P(95 ≤ X ≤ 101) = P(X ≤ 101) - P(X < 95) = 0.9983 - 0.0017 = 0.9966
Hence, the probability that less than 101 schemes will succeed is 0.9983. The probability that more than 95 schemes will succeed is 0.0018. The probability that between 95 and 101 schemes will succeed is 0.9966.
Learn more about Binomial distribution:
https://brainly.com/question/15246027
#SPJ11
In 14 days, Lin's sister will be paid $430 and will deposit it into her checking account. If there are no other transactions besides this deposit and the daily fee, will Lin continue to be charged $5.95 each day after this deposit is made? Explain or show your reasoning.
Answers
The equation, fine is $5*86 = 430so 430-430 = 0, Lin's account balance is much above zero (0), so she won't be charged $5.95 each day.
What is equation?A mathematical equation is a formula that joins two statements and uses the equal symbol (=) to indicate equality. A mathematical statement that establishes the equality of two mathematical expressions is known as an equation in algebra. For instance, in the equation 3x + 5 = 14, the equal sign places the variables 3x + 5 and 14 apart. The relationship between the two sentences on either side of a letter is described by a mathematical formula. Often, there is only one variable, which also serves as the symbol. for instance, 2x – 4 = 2.
Lin's sister will be paid $430
here are no other transactions besides this deposit and the daily fee
since fine is $5*86 = 430
so 430-430 = 0
hence,
Lin's account balance is much above zero (0), so she won't be charged $5.95 each day. However, if her account balance were to drop below zero, she would be charged for any further daily deposits made.
To know more about equation visit:
https://brainly.com/question/649785
#SPJ1
In which quadrant are all coordinates positive?

Answers
Answer:
Quadrant 1
Step-by-step explanation:
Quadrant 1 has positive x and y.
assume that the hourly cost to operate a commercial airplane follows the normal distribution with a mean of $3,403 per hour and a standard deviation of $398.what is the operating cost for the lowest 2% of the airplanes?
Answers
Answer:
$2,611.9.
Step-by-step explanation:
To find the operating cost for the lowest 2% of the airplanes, we need to find the corresponding z-score from the standard normal distribution using a z-table.
Using the formula:
z = (x - μ) / σ
where x is the cost we are interested in, μ is the mean cost, and σ is the standard deviation.
For the lowest 2% of airplanes, the z-score can be found by looking up the area to the left of z in the z-table. This area is 0.02.
Looking up 0.02 in the z-table gives a z-score of approximately -2.05.
So we have:
-2.05 = (x - 3403) / 398
Solving for x, we get:
x = -2.05 * 398 + 3403 = $2,611.9
Therefore, the operating cost for the lowest 2% of the airplanes is approximately $2,611.9.
pls help asap if you can!!

Answers
The ∆ABC is an isosceles triangle and have the base angles m∠A and m∠C equal to 51° and the angle m∠B is equal to 78°.
What is an Isosceles triangleAn isosceles triangle have the measure of its base angles to be equal, and the sum of the interior angles sum up to 180°.
Given that sides AB ≅ BC, then the triangle ∆ABC has two sides with similar length and base angles so;
angles m∠A and m∠C are the base angles are both equal to 51°
m∠B = 180° - (51 + 51)° {sum of interior angles of a triangle}
m∠B = 180° - 102°
m∠B = 78°
Therefore, the isosceles triangle ∆ABC have the base angles m∠A and m∠C equal to 51° and the angle m∠B is equal to 78°.
Read more about Isosceles triangle here:https://brainly.com/question/1475130
#SPJ1
The ratio of basketballs to volleyball in the gym is 3 to 5. If there are 60 volleyball in the gym, how many basketballs are there?
Answers
|-x-15 | = | 5x - 23 |
Answers
Answer:
Let's solve your equation step-by-step.
|−x−15|=|5x−23|
Solve Absolute Value.
|−x−15|=|5x−23|
We know either−x−15=5x−23or−x−15=−(5x−23)
−x−15=5x−23(Possibility 1)
−x−15−5x=5x−23−5x(Subtract 5x from both sides)
−6x−15=−23
−6x−15+15=−23+15(Add 15 to both sides)
−6x=−8
−6x
−6
=
−8
−6
(Divide both sides by -6)
x=
4
3
−x−15=−(5x−23)(Possibility 2)
−x−15=−5x+23(Simplify both sides of the equation)
−x−15+5x=−5x+23+5x(Add 5x to both sides)
4x−15=23
4x−15+15=23+15(Add 15 to both sides)
4x=38
4x
4
=
38
4
(Divide both sides by 4)
x=
19
2
Check answers. (Plug them in to make sure they work.)
x=
4
3
(Works in original equation)
x=
19
2
(Works in original equation)
Answer:
x=
4
3
or x=
19
2
Step-by-step explanation:
Answer:
x = 4/3
Step-by-step explanation:
|-x-15 | = | 5x - 23 |
take square root
√-x-15 = √ 5x - 23
than take square
(√-x-15 )² = (√ 5x - 23)²
than,
-x -15 = 5x - 23
-15 = x + 5x - 23 ( add x on both sides )
-15 + 23 = 6x ( add 23 on both sides )
8 = 6x
8/6 = x (divide 6 on both sides )
x = 4/3
PLEASE HELP ME WITH THIS!!!!!!!!!!!!!!!!!!

Answers
Answer:
You may use cos 60° or sin 30°. Let's use cos 60°.
cos 60° = opp/hyp = (2 mm)/j
or
j = (2 mm)/(cos 60°) = 4 mm
stuck on this math question for years,! if anyone helps 12 points !!!

Answers
Answer:
3
Step-by-step explanation:
There are 4.5 diamonds, which represent 9 hours in total.
This corresponds to 9/3 = 3 circles.
Answer:
3 circles
Step-by-step explanation:
For the pig, it's 4.5 squares. Each square is two hours, and 4.5*2 is 9. Each circle is 3 hours, and 9 divided by 3 is 3. Therefore, the answer is 3 circles.
HELP
im dont know this

Answers
Answer:
C
Step-by-step explanation:
use 0 and 3 for example:
replace x with 0 give you 2*0=0
add 0 with 3 and you get 3
Un mes Rodrigo alquiló 2 películas y 3 juegos de video con un costo total de $230.50. El próximo mes él alquiló 4 películas y 8 juegos de video con un costo total de $580.00. Hallar el costo de alquiler de cada película y de cada juego de video.
Answers
Answer:
El costo de alquiler de cada película es $26 y el costo de alquiler de cada juego de video es $59.50.
Step-by-step explanation:
A partir de la información proporcionada, puedes escribir las siguientes ecuaciones:
4x+8y=580 (1)
2x+3y=230.50 (2), donde:
"x" es el costo de alquiler de cada película y "y" es el costo de alquiler de cada juego de video.
Primero, puedes despejar x en (1):
4x=580-8y
x=145-2y (3)
Segundo, debes reemplazar (3) en (2):
2(145-2y)+3y=230.50
290-4y+3y=230.50
290-230.50=4y-3y
y=59.50
Tercero, debes reemplazar el valor de y en (3) para encontrar el valor de x:
x=145-2(59.50)
x145-119
x=26
De acuerdo a esto, la respuesta es que el costo de alquiler de cada película es $26 y el costo de alquiler de cada juego de video es $59.50.
A jewelry store has 212.75 ounces of 14-carat gold in stock. (a) how many custom necklaces can be manufactured if each requires 2 7/8 ounces of gold? (b) if gold is currently selling for $1,050 per ounce, how much is the gold in each necklace worth (in $)?
Answers
Answer:
a. The number of custom necklaces that can be manufactured if each requires 2 7/8 ounces of gold is 74 necklaces.
b. The value of the gold in each necklace is $1761
Step-by-step explanation:
(a) Number of necklaces
2\(7/8\) ounces of gold=2.875
No of necklaces=212.75oz x 1 necklaces/2.875oz
=74 necklaces
(b)Value of gold in each necklace
There are 2.875 oz of 14K gold in each necklace. Pure gold is 24K.
Mass of pure gold=2.875oz x 14k/24k
=1.677083oz
Pure 24K gold is worth $1050/oz.
Value of pure gold=1.677oz x 1050/1oz
= 1760.9 dollars
The value of the gold in each necklace is $1761
#SPJ4
Learn more on
https://brainly.com/question/12983156
The number of custom necklaces that can be manufactured if each requires 2 7/8 ounces of gold is 74 necklaces and the value of the gold in each necklace is $ 1761.
2 ounces of gold = 2.875 oz.
Number of necklaces = 212.75 oz. x 1 necklaces / 2.875 oz.
= 74 necklaces
Value of gold in each necklace
There are 2.875 oz. of 14K gold in each necklace.
Mass of pure gold=2.875 oz. x 14 k / 24 k
= 1.677083 oz.
Pure 24K gold is worth $ 1050 / oz.
Value of pure gold= 1.677oz x 1050 / 1oz
= 1760.9 dollars
The value of the gold in each necklace is $1761
Therefore, the number of custom necklaces that can be manufactured if each requires 2 7/8 ounces of gold is 74 necklaces and the value of the gold in each necklace is $ 1761.
Learn more about mass here:
https://brainly.com/question/26150306
#SPJ4
Find the complete solution for each of the following PDEs. (a) 2uxx+5uxy−12uyy=0 (b) 9uxx−12uxy+4uyy=0. (c) uxx−uxy−6uyy=xsiny. (d) uxx+uxy−6uyy=xy. (e) uxx−2uxy=cos2x. sin3y. (f) uxx−uxy+uy=x2+y2. (g) uxxxx−2uxxyy+uyyyy=ex−2y.
Answers
(a) The given partial differential equation (PDE) 2uxx + 5uxy - 12uyy = 0 can be solved using the method of characteristics.
(b) The given PDE 9uxx - 12uxy + 4uyy = 0 can be solved using the method of characteristics.
(c) The given PDE uxx - uxy - 6uyy = xsiny can be solved using the method of variation of parameters.
(d) The given PDE uxx + uxy - 6uyy = xy can be solved using the method of separation of variables.
(e) The given PDE uxx - 2uxy = cos(2x)sin(3y) can be solved using the method of separation of variables.
(f) The given PDE uxx - uxy + uy = x^2 + y^2 can be solved using the method of Green's functions.
(g) The given PDE uxxxx - 2uxxyy + uyyyy = ex - 2y can be solved using the method of separation of variables.
Partial differential equations (PDEs) are equations that involve partial derivatives of an unknown function with respect to multiple variables. Solving PDEs involves finding a function that satisfies the given equation. Each of the given PDEs can be solved using different methods based on the nature of the equation.
In PDE (a), the method of characteristics can be used to solve it. This method involves finding characteristic curves along which the PDE can be reduced to a system of ordinary differential equations. By solving this system, we can obtain the solution to the PDE.
PDE (b) can also be solved using the method of characteristics, similar to PDE (a). The characteristic curves will provide the necessary information to solve the equation.
PDE (c) requires the method of variation of parameters. This method involves assuming a particular solution and then finding a complementary solution using a trial function. By combining these solutions, we can obtain the complete solution to the PDE.
PDE (d) can be solved using the method of separation of variables. This method involves assuming a solution of the form u(x, y) = X(x)Y(y) and then substituting it into the PDE. By separating the variables and solving the resulting ordinary differential equations, we can find the complete solution.
PDE (e) can also be solved using the method of separation of variables. By assuming a solution of the form u(x, y) = X(x)Y(y) and substituting it into the PDE, we can separate the variables and solve the resulting ordinary differential equations to obtain the solution.
PDE (f) requires the method of Green's functions. This method involves finding a Green's function for the given PDE and then using it to represent the solution as an integral involving the Green's function and the given source term.
PDE (g) can be solved using the method of separation of variables. By assuming a solution of the form u(x, y) = X(x)Y(y) and substituting it into the PDE, we can separate the variables and solve the resulting ordinary differential equations to obtain the complete solution.
Learn more about partial differential equation (PDE)
brainly.com/question/14728084
#SPJ11
How many triangles can be drawn with one 90o angle, a 70° angle, and an included side measuring 3 inches? Explain. Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
Answers
Answer:
2
Step-by-step explanation:
This is because any of the sides can be the one measuring 3 inches. Since it is a triangle, the sum of angles is 180. Let the third angle be x.
So, x + 90° + 70° = 180°
x + 160° = 180°
x = 180° - 160°
x = 20°
So, the third angle is 20°.
If the included side is a side other than the hypotenuse side, we can find it by applying the sine rule.
The included side can be either side other than the hypotenuse.
Also, either of the third angle in each triangle can be 20°
So, we have two sides and two triangles.
If the included side is the hypotenuse side, we use Pythagoras' theorem to find the length of the other two sides (and they must be equal)since the angle between the two sides is a right-angle, that is, 90°.
Since the other two angles are not equal, we cannot have a triangle with two equal sides and an hypotenuse. That is, we cannot have an isosceles triangle. So, no third triangle.
So, the total number of triangles that can be drawn with one 90° angle, a 70° angle and an included side measuring 3 inches is 2.
y=−5x2+ 6x− 3 y=−4x− 3
using elimination or subsutution
Answers
Step-by-step explanation:
My math is terrible but I think u should eliminate and substitute.
I think the answer is:2x-4y=13
START BY USING BODMAS
Bracketsofdivisionmultiplicationadditionsubtractiony=-(10)+6x-3y=-4x-3
{3+10=13}
{3y+y=4y}
{6x-4x=2x}
4y=+2x-13
=2x-4y=13
I'M NOT SURE OF THE ANSWER THOUGH
Find the absolute maximum and absolute minimum values of the function f(x)=x^3−12x^2−27x+8 over each of the indicated intervals.
(a) Interval = [−2,0]. (b) Interval = [1,10]. (c) Interval = [−2,10].
Answers
The value of Absolute maximum are (a) 8, (b) -30.36, (c) -10 and the Absolute minimum are (a) -10, (b) -362.39, (c) -362.39.
We are given a function:f(x) = x³ - 12x² - 27x + 8We need to find the absolute maximum and absolute minimum values of the function f(x) over each of the indicated intervals. The intervals are:
a) Interval = [-2, 0]
b) Interval = [1, 10]
c) Interval = [-2, 10]
Let's begin:
(a) Interval = [-2, 0]
To find the absolute max/min, we need to find the critical points in the interval and then plug them in the function to see which one produces the highest or lowest value.
To find the critical points, we need to differentiate the function:f'(x) = 3x² - 24x - 27
Now, we need to solve the equation:f'(x) = 0Using the quadratic formula, we get: x = (-b ± √(b² - 4ac)) / 2a
Substituting the values of a, b, and c, we get:
x = (-(-24) ± √((-24)² - 4(3)(-27))) / 2(3)x = (24 ± √(888)) / 6x = (24 ± 6√37) / 6x = 4 ± √37
We need to check which critical point lies in the interval [-2, 0].
Checking for x = 4 + √37:f(-2) = -10f(0) = 8
Checking for x = 4 - √37:f(-2) = -10f(0) = 8
Therefore, the absolute max is 8 and the absolute min is -10.(b) Interval = [1, 10]
We will follow the same method as above to find the absolute max/min.
We differentiate the function:f'(x) = 3x² - 24x - 27
Now, we need to solve the equation:f'(x) = 0Using the quadratic formula, we get: x = (-b ± √(b² - 4ac)) / 2a
Substituting the values of a, b, and c, we get:
x = (-(-24) ± √((-24)² - 4(3)(-27))) / 2(3)
x = (24 ± √(888)) / 6
x = (24 ± 6√37) / 6
x = 4 ± √37
We need to check which critical point lies in the interval [1, 10].
Checking for x = 4 + √37:f(1) = -30.36f(10) = -362.39
Checking for x = 4 - √37:f(1) = -30.36f(10) = -362.39
Therefore, the absolute max is -30.36 and the absolute min is -362.39.
(c) Interval = [-2, 10]
We will follow the same method as above to find the absolute max/min. We differentiate the function:
f'(x) = 3x² - 24x - 27
Now, we need to solve the equation:
f'(x) = 0
Using the quadratic formula, we get: x = (-b ± √(b² - 4ac)) / 2a
Substituting the values of a, b, and c, we get:
x = (-(-24) ± √((-24)² - 4(3)(-27))) / 2(3)x = (24 ± √(888)) / 6x = (24 ± 6√37) / 6x = 4 ± √37
We need to check which critical point lies in the interval [-2, 10].
Checking for x = 4 + √37:f(-2) = -10f(10) = -362.39
Checking for x = 4 - √37:f(-2) = -10f(10) = -362.39
Therefore, the absolute max is -10 and the absolute min is -362.39.
Learn more about function at
https://brainly.com/question/31956232
#SPJ11
The value of the test statistic for the test H0: μ = 3.8, Ha : μ > 3 with n = 52, x⎯⎯ = 4.2 and s = 1.9 is
Answers
The value of the test statistic for the test is 1.52
How to determine the value of the test statistic for the test?From the question, we have the following parameters that can be used in our computation:
H0: μ = 3.8, Ha : μ > 3 with n = 52, x⎯⎯ = 4.2 and s = 1.9
The above parameters mean that
Sample mean = 3.8Number of samples = 52x = 4.2Standard deviation = 1.9The value of the test statistic for the test is calculated as
\(t = \frac{x - \mu_0}{s/\sqrt n}\)
Substitute the known values in the above equation
\(t = \frac{4.2 - 3.8}{1.9/\sqrt {52}}\)
Evaluate the equation
t = 1.52
Read more about test statistic at
https://brainly.com/question/4621112
#SPJ1
For the following exercises, sketch the curves below by eliminating the parameter t. Give the orientation of the curve. 1. x=t2+2t,y=t+1 2. x=cos(t),y=sin(t),(0,2π] 3. x=2t+4,y=t−1 4. x=3−t,y=2t−3,1.5≤t≤3 For the following exercises, eliminate the parameter and sketch the graphs. 5. x=2t2,y=t4+1
Answers
y =\((x/2)^2 + 1 or y = (x/2)^2 + 1\)
The curve represents a parabola opening upwards. It is symmetric about the y-axis.
Let's eliminate the parameter t and sketch the curves for each exercise:
1. x = t^2 + 2t, y = t + 1
To eliminate the parameter t, we can solve the first equation for t and substitute it into the second equation:
t^2 + 2t = x
t = -1 ± √(x + 1)
Substituting the expression for t into the equation y = t + 1, we get:
y = (-1 ± √(x + 1)) + 1
y = -√(x + 1) or y = √(x + 1)
The curve represents two branches of a parabola opening upwards. It is symmetric about the y-axis.
2. x = cos(t), y = sin(t), (0, 2π]
Eliminating the parameter t, we obtain:
\(x^2 + y^2 = cos^2(t) + sin^2(t) \\= 1\)
The curve represents a circle centered at the origin with a radius of 1. It covers a full revolution (360 degrees or 2π) in the counterclockwise direction.
3. x = 2t + 4, y = t - 1
By eliminating the parameter t, we have:
t = (x - 4) / 2
Substituting this expression into the equation for y, we get:
y = ((x - 4) / 2) - 1
y = (x - 6) / 2
The curve represents a line with a slope of 1/2 and a y-intercept of -3. It is inclined upwards from left to right.
4. x = 3 - t, y = 2t - 3, 1.5 ≤ t ≤ 3
Eliminating the parameter t, we have:
t = 3 - x
Substituting this expression into the equation for y, we get:
y = 2(3 - x) - 3
y = 6 - 2x - 3
y = -2x + 3
The curve represents a line with a slope of -2 and a y-intercept of 3. It is inclined downwards from left to right.
\(5. x = 2t^2, y = t^4 + 1\)
To eliminate the parameter t, we can solve the first equation for t and substitute it into the second equation:
t^2 = x/2
t = ±√(x/2)
Substituting the expressions for t into the equation y = t^4 + 1, we get:
y = (√(\(x/2))^4\) + 1 or y = (-√\((x/2))^4\) + 1
\(y = (x/2)^2 + 1 or y = (x/2)^2 + 1\)
To know more about equation visit:
brainly.com/question/29538993
#SPJ11
A bar of cast iron 18.125" long has been tapered from a diameter of 0.983" to a diameter of 2.74". What is the difference in diameter between the two ends?
Answers
Answer:
The difference in diameter between the two ends is 1.757''
Step-by-step explanation:
Given;
length of a bar of cast iron, L = 18.125"
initial diameter of the bar, d₁ = 0.983"
final diameter of the bar, d₂ = 2.74"
The difference in diameter between the two ends of the bar is calculated as;
difference in diameter = d₂ - d₁
difference in diameter = 2.74" - 0.983"
difference in diameter = 1.757''
Therefore, the difference in diameter between the two ends is 1.757''
I need help with this plzz
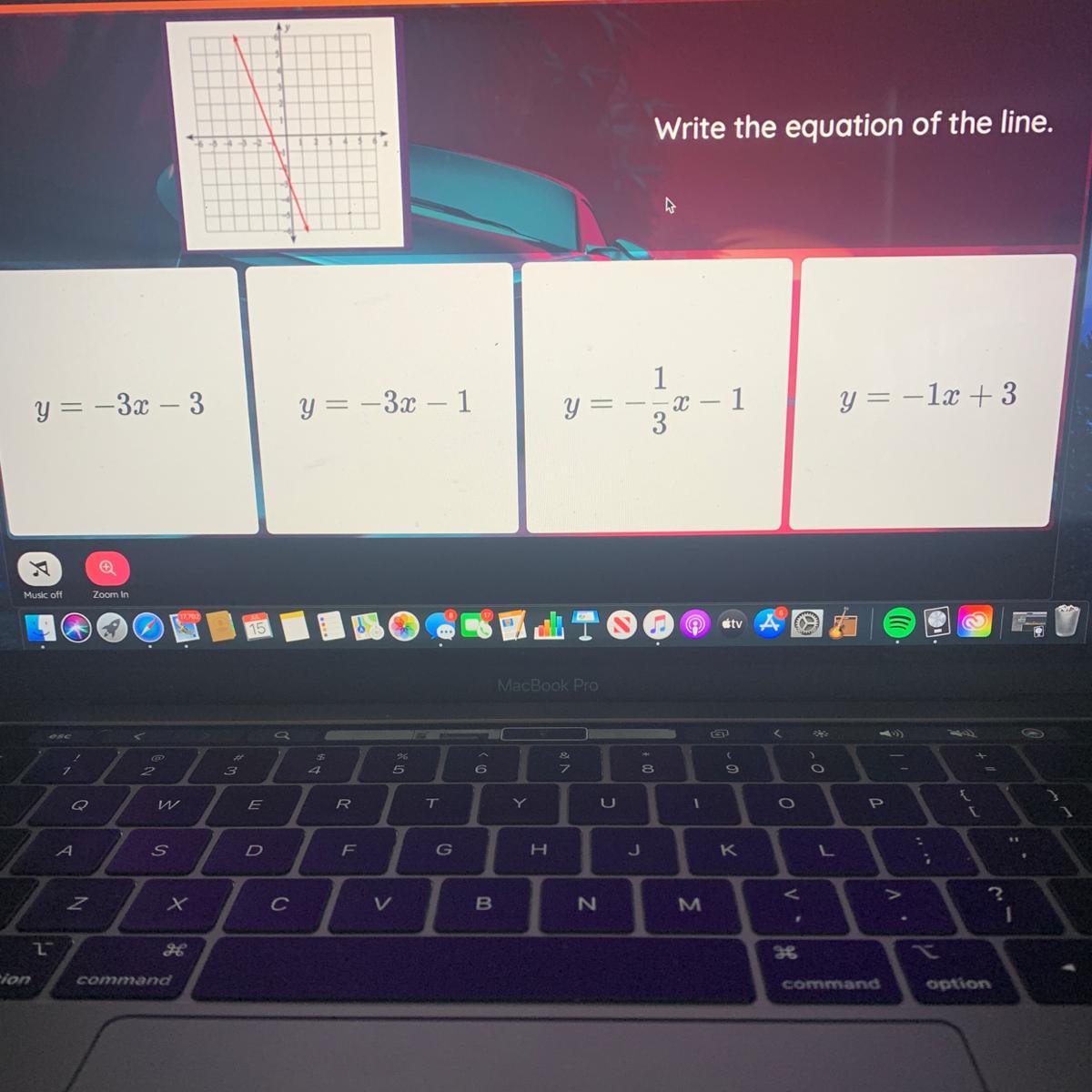
Answers
Answer:
The answer is y=-3x-3.
For every computer that is sold, Kendall receives $ 250 in commissions. The amount of commissions that Peter receives can be represented by the function y = 225x where y is his commission and x is the number of computers sold. How much more does Kendall receive in commissions than Peter if they both sell 5 computers ?
Answers
Kendall receives $125 more in commissions than Peter if they both sell 5 computers
The given functions are;
For Kendall: f(x) = 250x
For Peter: g(x) = 225x
Let's put x=5 in the given functions;
For Kendall: f(x) = 250x
= 250(5)
= $1250
For Peter: g(x) = 225x
= 225(5)
= $1125
Kendall receives $1250 in commissions and Peter receives $1125 in commissions.
Therefore, the difference between their commissions is; $1250 - $1125 = $125.
Therefore, Kendall receives $125 commission than Peter.
learn more about computer from given link
https://brainly.com/question/24540334
#SPJ11
Suppose you're doing a hypothesis test where the level of significance is 0.05, and you get a P-value of 0.165. What would your decision be in Step 4?

Answers
Answer;
Reject the null hypothesis
Explanation;
Here, we are having a situation in which the level of significance is less than the p-value
In this type of case, what we simply do is to reject the null hypothesis and accept the alternative hypothesis
Hence, simply put, we are going to reject the nulll hypothesis
PLEASE HELP ASAP!!!!!
Rewrite the expression 20x + 25 as the product of two factors.
Answers
Answer:
5 (4 x + 5)
That is the answer
5 is a factor if 20 and 25 and 4x + 5 cannot be furthor be simplified.
find the probability that a sample of 33 randomly selected adults in us has a mean weight greater than 151.52 lbs.
Answers
The probability that a sample of 33 randomly selected adults in the US has a mean weight greater than 151.52 lbs is:
38.21%.
To find the probability that a sample of 33 randomly selected adults in the US has a mean weight greater than 151.52 lbs, we need to use the Central Limit Theorem. Assuming that the population standard deviation is known or the sample size is large enough (greater than or equal to 30), the distribution of the sample means will be approximately normal.
First, we need to calculate the standard error of the mean (SEM) using the formula:
SEM = standard deviation / square root of sample size
Let's assume that the population standard deviation is 30 lbs (this is just an estimate) and the sample size is 33. Then,
SEM = 30 / sqrt(33) = 5.22 lbs
Next, we need to calculate the z-score using the formula:
z = (sample mean - population mean) / SEM
Let's assume that the population mean is 150 lbs (again, just an estimate). Then,
z = (151.52 - 150) / 5.22 = 0.30
Finally, we can use a standard normal distribution table or calculator to find the probability that the z-score is greater than 0.30. This is equivalent to finding the area under the standard normal curve to the right of 0.30. Using a standard normal distribution table or calculator, we find that the probability is approximately 0.3821 or 38.21%.
Therefore, the probability that a sample of 33 randomly selected adults in the US has a mean weight greater than 151.52 lbs is approximately 38.21%.
To learn more about probability visit : https://brainly.com/question/13604758
#SPJ11