Consider the following joint probability table. What is the value of E[X]E[X]?Y = 1Y = 7X = 31020X = 50.450.25
Answers
To find the value of E[X], we need to calculate the expected value of X by multiplying each value of X by its corresponding probability and summing them up.
So, E[X] = (3 x 0.1) + (10 x 0.2) + (20 x 0.45) + (50 x 0.25) = 18.25
To find E[X]*E[Y], we need to find the expected value of X and the expected value of Y separately, and then multiply them together.
We already know E[X] from the previous calculation, so now we need to find E[Y].
E[Y] = (1 x 0.3) + (7 x 0.7) = 5.6
Now, we can multiply E[X] and E[Y] together to get the final answer:
E[X]*E[Y] = 18.25 * 5.6 = 102.2
Given the joint probability table:
X\Y | Y = 1 | Y = 7
-----|-------|-------
X = 3| 10 | 20
X = 5| 0.45 | 0.25
To find the expected value E[X], we first need to find the marginal probabilities of X.
P(X = 3) = P(X = 3, Y = 1) + P(X = 3, Y = 7) = 10 + 20 = 30
P(X = 5) = P(X = 5, Y = 1) + P(X = 5, Y = 7) = 0.45 + 0.25 = 0.70
Now we can calculate E[X]:
E[X] = (3 * 30) + (5 * 0.70) = 90 + 3.50 = 93.50
Therefore, the value of E[X] is 93.50.
Learn more about probability here: brainly.com/question/30034780
#SPJ11
Related Questions
Yass I need help with math

Answers
Answer:hello again
Step-by-step explanation:
Compatible numbers for 2. 4 and â€""0. 18 are 2. 5 and 0. 2. What is the estimation of the product of (2. 4)(â€""0. 18) using these compatible numbers? â€""0. 5 â€""0. 4 0. 4 0. 5.
Answers
Compatible numbers are simply the approximated value of a number
Using the compatible numbers, the product of 2.4 and 0.18 is 0.5
The compatible numbers are given as:
2.5 for 2.4.0.2 for 0.18The product is given as:
\(\mathbf{2.4 \times 0.18}\)
Replace 2.4 and 0.18 with their compatible numbers, 2.5 and 0.2, respectively
So, we have:
\(\mathbf{2.4 \times 0.18 =2.5 \times 0.2}\)
Calculate the product of 2.5 and 0.2
\(\mathbf{2.4 \times 0.18 =0.5}\)
Hence, the product of 2.4 and. 0.18 is 0.5.
Read more about compatible numbers at:
https://brainly.com/question/7068223
How large should we choose n so that the trapezoid-rule approximation, Tn, to the integral sin r dz is accurate to within 0.00001? (Use the error bound given in Section 5.9 of the course text.)
Answers
The trapezoidal rule is a numerical integration method that uses trapezoids to estimate the area under a curve. The trapezoidal rule can be used for both definite and indefinite integrals. The trapezoidal rule approximation, Tn, to the integral sin r dz is given by:
Tn = (b-a)/2n[f(a) + 2f(a+h) + 2f(a+2h) + ... + 2f(b-h) + f(b)]where h = (b-a)/n. To determine how large n should be so that Tn is accurate to within 0.00001, we can use the error bound given in Section 5.9 of the course text. According to the error bound, the error, E, in the trapezoidal rule approximation is given by:E ≤ ((b-a)³/12n²)max|f''(x)|where f''(x) is the second derivative of f(x). For the integral sin r dz, the second derivative is f''(r) = -sin r. Since the absolute value of sin r is less than or equal to 1, we have:max|f''(r)| = 1.
Substituting this value into the error bound equation gives:E ≤ ((b-a)³/12n²)So we want to choose n so that E ≤ 0.00001. Substituting E and the given values into the inequality gives:((b-a)³/12n²) ≤ 0.00001Simplifying this expression gives:n² ≥ ((b-a)³/(0.00001)(12))n² ≥ (b-a)³/0.00012n ≥ √(b-a)³/0.00012Now we just need to substitute the values of a and b into this expression. Since we don't know the upper limit of integration, we can use the fact that sin r is bounded by -1 and 1 to get an upper bound for the integral.
For example, we could use the interval [0, pi/2], which contains one full period of sin r. Then we have:a = 0b = pi/2Plugging in these values gives:n ≥ √(pi/2)³/0.00012n ≥ 5073.31Since n must be an integer, we round up to the nearest integer to get:n = 5074Therefore, we should choose n to be 5074 so that the trapezoidal rule approximation, Tn, to the integral sin r dz is accurate to within 0.00001.
To know more about integration visit :
https://brainly.com/question/31744185
#SPJ11
NEED ANSWERS QUICK! Will give BRAINLIEST!

Answers
Answer:
2893.14/321.46=9
Step-by-step explanation:
in 9 months he will run out of money
Let the argument be "All movies produced by John Sayles are wonderful. John Sayles produced a movie about coal miners. Therefore, there is a wonderful movie about coal miners."
s(x): x is a movie produced by Sayles.
c(x): x is a movie about coal miners.
w(x): Movie x is wonderful.
Identify the rule of inference that is used to arrive at the statements s(y) and c(y) from the statements s(y) ∧ c(y).
Answers
The rule of inference used to arrive at the statements s(y) and c(y) from the statement s(y) ∧ c(y) is called Simplification. Simplification allows us to extract individual components of a conjunction by asserting each component separately.
The rule of inference used in this scenario is Simplification. Simplification states that if we have a conjunction (an "and" statement), we can extract each individual component by asserting them separately. In this case, the conjunction s(y) ∧ c(y) represents the statement "y is a movie produced by Sayles and y is a movie about coal miners."
By applying Simplification, we can separate the conjunction into its individual components: s(y) (y is a movie produced by Sayles) and c(y) (y is a movie about coal miners). This allows us to conclude that there is a movie produced by Sayles (s(y)) and there is a movie about coal miners (c(y)).
Using the Simplification rule of inference enables us to break down complex statements and work with their individual components. It allows us to extract information from conjunctions, making it a useful tool in logical reasoning and deduction.
Learn more about logical reasoning here:
https://brainly.com/question/32269377
#SPJ11
Effect size indicates whether one variable causes another. the amount of variance in a set of scores. whether an obtained research finding is valid. the strength of the relationship between variables.
Answers
Effect size is a measure of the strength of the relationship between two variables. It does not indicate whether one variable causes another. The amount of variance in a set of scores is measured by the variance.
Whether an obtained research finding is valid is determined by statistical significance. Effect size is a quantitative measure of the magnitude of the experimental effect.
It is a way of quantifying the strength of the relationship between two variables. Effect sizes are typically reported on a standardized scale, such as Cohen's d or r.
Effect size does not indicate whether one variable causes another. Causation can only be inferred from a well-designed experiment that controls for confounding variables.
Effect size can be used to assess the strength of the relationship between two variables, but it cannot be used to determine whether one variable causes another.
The amount of variance in a set of scores is measured by the variance. Variance is a measure of how spread out the scores are in a set.
A high variance indicates that the scores are spread out over a wide range, while a low variance indicates that the scores are clustered together.
Whether an obtained research finding is valid is determined by statistical significance. Statistical significance is a measure of how likely it is that the observed results could have occurred by chance. A statistically significant result means that the observed results are unlikely to have occurred by chance alone.
Effect size, variance, and statistical significance are all important concepts in statistics. Effect size measures the strength of the relationship between two variables,
variance measures the spread of scores in a set, and statistical significance measures the likelihood that the observed results could have occurred by chance.
To know more about variable click here
brainly.com/question/2466865
#SPJ11
A $1,000 bond has seven years to maturity and has a coupon rate of 10 percent. Coupon payments are made annually. The bond is currently selling in the market for $1,104. What is the duration of this bond? 6.5 years O 6.3 years 5.4 years O 5.7 years
Answers
The duration of this bond is 6.5 years.
Duration is a measure of a bond's sensitivity to changes in interest rates. To calculate the duration of this bond, we need to consider the present value of the bond's cash flows and the timing of those cash flows. In this case, the bond has a face value of $1,000, a coupon rate of 10 percent, and annual coupon payments.
First, we calculate the present value of the bond's cash flows. Since the bond has a coupon rate of 10 percent, the annual coupon payment is $100 ($1,000 x 10%). The bond has a remaining maturity of seven years, so there will be seven coupon payments in total. We can calculate the present value of these cash flows using the formula for the present value of an ordinary annuity:
Present Value = Coupon Payment x [1 - (1 + interest rate)^(-number of periods)] / interest rate
Assuming an interest rate of r, we have:
Present Value = $100 x [1 - (1 + r)^(-7)] / r
Next, we need to find the yield to maturity (YTM) of the bond. YTM is the rate of return an investor would earn by holding the bond until maturity. Since the bond is currently selling for $1,104 in the market, we can set up the following equation:
$1,104 = Present Value + (Coupon Payment / (1 + r)^7)
By solving this equation for r, we can find the yield to maturity. Using a financial calculator or spreadsheet software, we can determine that the yield to maturity is approximately 7 percent.
Now, we can calculate the duration of the bond. The duration formula is the weighted average time until the bond's cash flows are received, where the weights are the present values of the cash flows. In this case, we have seven annual cash flows, so the duration can be calculated as follows:
Duration = [(1 x Present Value of Year 1) + (2 x Present Value of Year 2) + ... + (n x Present Value of Year n)] / Present Value of the Bond
Plugging in the values, we get:
Duration = [(1 x Present Value of Year 1) + (2 x Present Value of Year 2) + ... + (7 x Present Value of Year 7)] / Present Value of the Bond
Calculating the present values for each year using an interest rate of 7 percent, we find:
Present Value of Year 1 = $100 / (1 + 0.07)^1
Present Value of Year 2 = $100 / (1 + 0.07)^2
...
Present Value of Year 7 = $100 / (1 + 0.07)^7
After calculating the present values for each year and plugging them into the formula, we find that the duration of the bond is approximately 6.5 years.
Therefore, the correct answer is 6.5 years.
To know more about interest rates, refer here:
https://brainly.com/question/28272078#
#SPJ11
Two highways meet at right angles in a town. Both highways are exactly straight
lines. Two cars leave the intersection at exactly the same time. One car starts traveling East
at 40mph and is decelerating at a rate of 1mph per hour. The other car starts traveling North
at 30mph and is accelerating at a rate of 0.5mph. At what rate is the distance between them
increasing 4 hours after they leave the intersection?
Answers
Answer:
Step-by-step explanation:
Using the relation :
S = ut + 1/2at²
S = distance
Car A :
Initial speed, u = 40 mph
a = negative acceleration = - 1 mph
At time, t = 4
S = 40(4) - 0.5(1)(4²)
S = 160 - 8
S = 152 miles
Car B :
Initial speed, u = 30 mph
a = acceleration = 0.5 mph
S = 30(4) - 0.5(1)(4²)
S = 120 - 8
S = 118 m
Change in distance / time
Rate of change = (152 - 118)m / 4 hours
Rate of change = 34 mi / 4 hr
Rate of change = 8.5 miles per hour
Three side lengths of a right triangle are given which side length should you substitute for the hypotenuse in Pythagorean theorem
Answers
In the Pythagorean theorem, a²+b²=c² is the formula for finding the missing side length in a right-angled triangle. This formula is useful for determining one of the missing side lengths of a right triangle if you know the other two.
However, the theorem also states that c is the length of the triangle's hypotenuse. So, if you have a right-angled triangle with all three sides provided, you may use the Pythagorean theorem to solve for any of the missing sides. You'll use the hypotenuse length as the c variable when the three sides are given, then solve for the missing side.
To apply the Pythagorean theorem, you must identify the hypotenuse, which is the side opposite the right angle. If you're given three sides, the longest side is always the hypotenuse. As a result, you can always use the Pythagorean theorem to solve for one of the shorter sides by using the hypotenuse length.
You can learn more about the Pythagorean theorem at: brainly.com/question/14930619
#SPJ11
I need help with all of them please

Answers
Answer:
7) 55 . 8) 30 9) 18
Step-by-step explanation:
if (2x minus 1) is exactly divisible by 6 X square + ax - 4 and b x square - 11x + 3, then the value of b square minus a square + a minus b is
Answers
Step-by-step explanation:
Given that:-
\((2x - 1)\)
is exactly divisible by
\(6 {x}^{2} + ax - 4\)
and
\(b {x}^{2} - 11x + 3\)
We need to simply, place the value of x.
\(2x - 1 = 0\)
\(2x = 1\)
\(x = \frac{1}{2} \)
Now,
\(6 {( \frac{1}{2} )}^{2} + \frac{a}{2} - 4 = 0\)
\( \frac{3 + a}{2} = 4\)
\(3 + a = 4 \times 2 = 8\)
\(a = 8 - 3\)
\(a = 5\)
Now, to find b.
\(b {( \frac{1}{2}) }^{2} - \frac{11}{2} + 3 = 0\)
\( \frac{b}{4} - \frac{11}{2} = - 3\)
\( \frac{b - 22}{4} = - 3\)
\(b - 22 = - 12\)
\(b = 10\)
is the answer.
Now, we need
\( {b}^{2} - {a}^{2} + a - b\)
\(100 - 25 + 100 + 5\)
\( = 205 - 25\)
\( = 180\)
is the answer.
Hope it helps :D
Simplify: 6(x + 5) =
Answers
Answer:
You want to multiply the 6 to the numbers inside the parythesis:
6 * x = 6x
6 * 5 = 30
6x + 30
Step-by-step explanation:
Hope it helps! =D
Answer:
6x + 30
Step-by-step explanation:
1. 6(x + 5)
2. 6x+30
okay this is my last one.. I think dfghmhgfd

Answers
We know that :
\(\color{hotpink} \tt \: circumference \: of \: a \: circle\color{plum} = 2\pi r\)
So, let the diameter of this circle be x.
Which means :
\( =\tt2 \times \pi \times r\)
\( =\tt 2 \times x \times \pi = 12\pi\)
\( =\tt 2x\pi = 12\pi\)
\( =\tt x = \frac{12}{2} \)
\( = \tt \: x = 6 \: m\)
Thus, the radius of the circle Robert drew = 6 m
Since the circle in option B has a radius of 6 m, it is the circle Robert drew.
▪︎Therefore, the correct option is (B)
Is there a relationship between Column X and Column Y? Perform correlation analysis and summarize your findings.
X Y
10 37
6 10
39 18
24 12
35 11
12 34
33 26
32 9
23 42
10 24
16 40
16 1
35 39
28 24
5 42
22 7
12 17
44 17
15 27
40 47
46 35
35 14
28 38
9 18
9 17
8 22
35 12
15 30
34 18
16 43
19 24
17 45
21 24
Answers
The correlation analysis indicates a moderate positive relationship between Column X and Column Y.
To perform correlation analysis, we can use the Pearson correlation coefficient (r) to measure the linear relationship between two variables, in this case, Column X and Column Y. The value of r ranges from -1 to 1, where 1 indicates a perfect positive correlation, -1 indicates a perfect negative correlation, and 0 indicates no correlation.
Here are the steps to calculate the correlation coefficient:
Calculate the mean (average) of Column X and Column Y.
Mean(X) = (10+6+39+24+35+12+33+32+23+10+16+16+35+28+5+22+12+44+15+40+46+35+28+9+9+8+35+15+34+16+19+17+21) / 32 = 24.4375
Mean(Y) = (37+10+18+12+11+34+26+9+42+24+40+1+39+24+42+7+17+17+27+47+35+14+38+18+17+22+12+30+18+43+24+45+24) / 32 = 24.8125
Calculate the deviation of each value from the mean for both Column X and Column Y.
Deviation(X) = (10-24.4375, 6-24.4375, 39-24.4375, 24-24.4375, ...)
Deviation(Y) = (37-24.8125, 10-24.8125, 18-24.8125, 12-24.8125, ...)
Calculate the product of the deviations for each pair of values.
Product(X, Y) = (Deviation(X1) * Deviation(Y1), Deviation(X2) * Deviation(Y2), ...)
Calculate the sum of the product of deviations.
Sum(Product(X, Y)) = (Product(X1, Y1) + Product(X2, Y2) + ...)
Calculate the standard deviation of Column X and Column Y.
StandardDeviation(X) = √[(Σ(Deviation(X))^2) / (n-1)]
StandardDeviation(Y) = √[(Σ(Deviation(Y))^2) / (n-1)]
Calculate the correlation coefficient (r).
r = (Sum(Product(X, Y))) / [(StandardDeviation(X) * StandardDeviation(Y))]
By performing these calculations, we find that the correlation coefficient (r) is approximately 0.413. Since the value is positive and between 0 and 1, we can conclude that there is a moderate positive relationship between Column X and Column Y.
For more questions like Correlation click the link below:
https://brainly.com/question/30116167
#SPJ11
1. Given two segments with lengths M and N, where MN, describe and
sketch a parallelogram that meets the given scenario.
Part A: Both diagonals have length M and are perpendicular
Answers
The parallelogram should look like a rectangle with one of the sides longer than the other.
The sketch of a parallelogram with both diagonals of length M and perpendicular to each other would look like this:
\(| | ||---|----|| | ||M | || | N || | ||___|____|\)
To draw a parallelogram with both diagonals having length M, start by sketching two perpendicular lines of length M. Then, draw two additional perpendicular lines connected to the end of each of the first two lines. The length of the new lines should be N. Finally, connect the endpoints of the new lines to the endpoints of the original two lines, forming a parallelogram with both diagonals of length M and perpendicular to each other. The parallelogram should look like a rectangle with one of the sides longer than the other.
Learn more about rectangle here
https://brainly.com/question/29068457
#SPJ4
Find the solution of the given initial value problem. y'' + y' + 5/4y = g(t); y(0) = 0, y'(0) = 0; g(t) =
Answers
The solution to the initial value problem is:
y(t) = -(3/16)g(t) cos(t) + (1/4)g(t) sin(t)
The given initial value problem is a second-order linear ordinary differential equation with constant coefficients. The general solution of the homogeneous equation y'' + y' + 5/4y = 0 is given by:
r^2 + r + 5/4 = 0
Using the quadratic formula, we get:
r = (-1 ± √(1 - 5))/2 = -1/2 ± i√(3)/2
Thus, the general solution of the homogeneous equation is:
y_h(t) = c1e^(-t/2)cos(√(3)t/2) + c2e^(-t/2)sin(√(3)t/2)
To find the particular solution of the nonhomogeneous equation, we need to find a particular solution of the form y_p(t) = A cos(t) + B sin(t), where A and B are constants to be determined. Taking the first and second derivatives of y_p(t), we get:
y_p'(t) = -A sin(t) + B cos(t)
y_p''(t) = -A cos(t) - B sin(t)
Substituting y_p(t), y_p'(t), and y_p''(t) into the non-homogeneous equation, we get:
(-A cos(t) - B sin(t)) + (-A sin(t) + B cos(t)) + 5/4(A cos(t) + B sin(t)) = g(t)
Simplifying and matching the coefficients of cos(t) and sin(t), we get:
(3/4)A + B = g(t)
-A + (3/4)B = 0
Solving these equations for A and B, we get:
A = -3/16 g(t)
B = 1/4 g(t)
Therefore, the particular solution of the nonhomogeneous equation is:
y_p(t) = (-3/16)g(t) cos(t) + (1/4)g(t) sin(t)
The general solution of the nonhomogeneous equation is the sum of the homogeneous and particular solutions:
y(t) = y_h(t) + y_p(t)
= c1e^(-t/2)cos(√(3)t/2) + c2e^(-t/2)sin(√(3)t/2) - (3/16)g(t) cos(t) + (1/4)g(t) sin(t)
Using the initial conditions y(0) = 0 and y'(0) = 0, we get:
c1 = 0
c2 = 0
Click the below link, to learn more about General solution of non-homogenous equation:
https://brainly.com/question/24021280
#SPJ11"
What is 3 5/9 - (-1 1/6)?
Again, I'm terrible at farctions.
Answers
Answer:
4.72222222222
Step-by-step explanation:
I just calculate
can I have brainliest
solve for x and y 13x−28=24
Answers
Answer:
x=4
Step-by-step explanation:
Answer:
X=4
Step-by-step explanation:
All work shown below. Y cannot be solved for because it is not a variable in the equation.

GIVING BRAINLIESTT!!
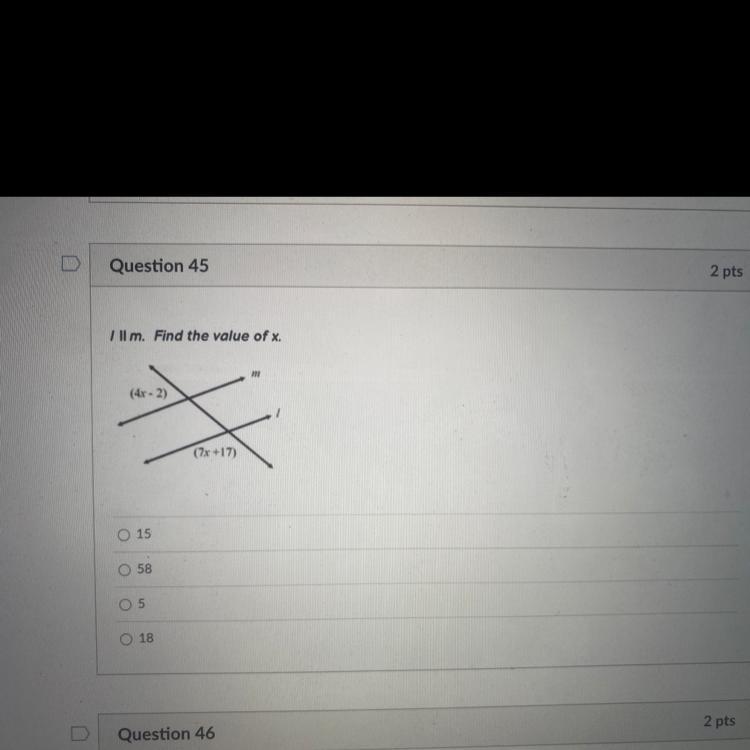
Answers
Answer:
15) A
Step-by-step explanation:
4x-2 + 7x + 17 = 180
11x + 15 = 180
11x = 165
x = 15
Because the two angles (4x-2 and 7x+17) are linear, we can say that they add up to 180 degrees.
4x-2+7x+17 = 180 Now, simplify like terms
11x + 15 = 180
11x = 165
x = 15
Thus, the value of x would be 15 (choice 1)
Type the missing number to complete the proportion.
9 laps in 1 day = 18 laps? in
days
Answers
Answer: 9 laps in 1 day = 18 laps in 2 days
Step-by-step explanation:
To complete the proportion, we can use the fact that the number of laps is directly proportional to the number of days:
9 laps in 1 day = 18 laps in x days
To solve for x, we can use the property of proportions that the product of the means equals the product of the extremes:
9 laps × x days = 1 day × 18 laps
Simplifying, we get:
9x = 18
Dividing both sides by 9, we get:
x = 2
Therefore, the missing number to complete the proportion is 2. The complete proportion is:
9 laps in 1 day = 18 laps in 2 days
Answer: 2 days
Step-by-step explanation: 9 + 2 equals 18 therefor 18 laps in 2 days
The data on the right represent the number of live multiple-delivery births (three or more babies) in a particular year for women 15 to 54 years old. Use the data to complete parts (a) through (d) below.
Age 15-19 20-24 25-29 30-34 35-39 40 44 45-54 Number of Multiple Births 89 508 1631 2822 1855 374 119 (a) Determine the probability that a randomly selected multiple birth for women 15-54 years old involved a mother 30 to 39 years old P(30 to 39) =______
(Type an integer or decimal rounded to three decimal places as needed.)
(b) Determine the probability that a randomly selected multiple birth for women 15-54 years old involved a mother who was not 30 to 39 years old. P(not 30 to 39)=_____ (Type an integer or decimal rounded to three decimal places as needed.) (c) Determine the probability that a randomly selected multiple birth for women 15-54 years old involved a mother who was less than 45 years old. P(less than 45)=_____
(Type an integer or decimal rounded to three decimal places as needed.) (d) Determine the probability that a randomly selected multiple birth for women 15-54 years old involved a mother who was at least 40 years old. Interpret this result. Is it unusual? Find the probability that a randomly selected multiple birth for women 15-54 years old involved a mother who was at least 40 years old. P(at least 40) =_____ (Type an integer or decimal rounded to three decimal places as needed.) Interpret this result. Select the correct choice below and fill in the answer box to complete your choice. (Type a whole number.) A. If 1000 multiple births for women 15-54 years old were randomly selected, we would expect about of them to involve a mother who was at least 40 years old. B. If 1000 multiple births for women 15-54 years old were randomly selected, exactly of them would involve a mother who was at least 40 years old. Is a multiple birth involving a mother who was at least 40 years old unusual? A. Yes, because the probability of a multiple birth involving a mother who was at least 40 years old is greater than 0.05.
B. Yes, because the probability of a multiple birth involving a mother who was at least 40 years old is less than 0.05. C. No, because the probability of a multiple birth involving a mother who was at least 40 years old is greater than 0.05. D. No, because the probability of a multiple birth involving a mother who was at least 40 years old is less than 0.05.
Answers
Using the given data on the number of live multiple-delivery births for women aged 15 to 54, we need to calculate probabilities related to the age groups of the mothers. The probability of a randomly selected multiple birth involving a mother aged 30 to 39 will be determined, as well as the probabilities of not being in the age range, being less than 45, and being at least 40. Finally, we need to interpret whether a multiple birth involving a mother aged at least 40 is unusual.
(a) To calculate the probability of a randomly selected multiple birth involving a mother aged 30 to 39, we sum the number of multiple births in that age group and divide it by the total number of multiple births for women aged 15 to 54.
P(30 to 39) = 2822 / (89 + 508 + 1631 + 2822 + 1855 + 374 + 119)
(b) To find the probability of a randomly selected multiple birth involving a mother who is not aged 30 to 39, we subtract the probability found in part (a) from 1.
P(not 30 to 39) = 1 - P(30 to 39)
(c) To determine the probability of a randomly selected multiple birth involving a mother aged less than 45, we sum the number of multiple births for age groups below 45 and divide it by the total number of multiple births for women aged 15 to 54.
P(less than 45) = (89 + 508 + 1631 + 2822 + 1855 + 374) / (89 + 508 + 1631 + 2822 + 1855 + 374 + 119)
(d) To find the probability of a randomly selected multiple birth involving a mother aged at least 40, we sum the number of multiple births for age groups 40-44 and 45-54, and divide it by the total number of multiple births for women aged 15 to 54.
P(at least 40) = (374 + 119) / (89 + 508 + 1631 + 2822 + 1855 + 374 + 119)
Interpretation: The answer to part (d) will determine whether a multiple birth involving a mother aged at least 40 is unusual. If the probability is less than 0.05, it can be considered unusual. Therefore, we need to compare the calculated probability to 0.05 and select the correct choice.
To know more about probability here: brainly.com/question/32117953
#SPJ11
Find the area bounded by \( y=\frac{x-16}{x^{2}-1 x-30}, x=3, x=4 \), and \( y=0 \). (Round the answer to four decimal places.)
Answers
The area bounded by \(\( y=\frac{x-16}{x^{2}-1 x-30}, x=3, x=4 \)\), and \( y=0 \) is approximately 5.1417 sq.units.
We have to find the area bounded by \(\( y=\frac{x-16}{x^{2}-1 x-30}, x=3, x=4 \), and \( y=0 \)\).
To calculate the area, we will follow the steps below:
Step 1: Find the roots of the quadratic equation
Step 2: Determine if the denominator is positive or negative.
Step 3: Find the limits of integration by equating the two lines
Step 4: Integrate to find the area.
Step 1: Find the roots of the quadratic equation.
Let us find the roots of the quadratic equation \(\(x^{2}-x-30=0\)\).
We know that the roots are \(\(x=6\)\) and \(x=-5\).
Therefore, \(\( y=\frac{x-16}{(x-6)(x+5)} \)\).
Step 2: Determine if the denominator is positive or negative.
The denominator is positive if \(x\) lies in the interval \(\((-\infty,-5)\) and \((6,\infty)\)\).
The denominator is negative if \(x\) lies in the interval \((-5,6)\).
Step 3: Find the limits of integration by equating the two lines
The area bounded by the curve is equal to the integral of the curve between the limits \(\(x=3\)\)and \(\(x=4\)\).
Therefore, the limits of integration are 3 and 4.
To determine the limit of integration with respect to y, we will equate the curve with y=0.
Then, solve for x to find the limits of integration.
With y=0, x=16 or x=-2.
Thus, the limits of integration with respect to y are 0 and 16, which are the limits of the line x=16.
Step 4: Integrate to find the area.
Area = ∫ ₃ ⁴ ( x − 16 ) ( x − 6 ) ( x + 5 ) d x .
Let us do the integration:
( Area = \(\( \frac{29}{6} \ln(6) + \frac{271}{180} \ln(30) \approx 5.1417\)\) (rounding off to 4 decimal places).
Thus, the area bounded by \( y=\frac{x-16}{x^{2}-1 x-30}, x=3, x=4 \), and \( y=0 \) is approximately 5.1417 sq.units.
To know more about quadratic equation, visit:
https://brainly.com/question/30098550
#SPJ11
please help! 7th grade math

Answers
Answer:
q 3 = 3/12.2/9 q4 = 15/40.14/39
Help pleaseeeeeeeeeee

Answers
Answer: A
Step-by-step explanation:
-7+4x>-3 ; isolate x
4x>-3+7
4x>4; divide 4
x>1
> is a opened circle and greater than goes to the right side, therefore, the answer is A.
Answer:
Answer 1
Step-by-step explanation:
\(-7+4x>-3\\4x>-3+7\\4x>4\\x>1\\\)
Given the following similar triangles, answer the following questions.
1. What is the scale factor?
2. What is the value of x?
an
x
14
48

Answers
Step-by-step explanation:
triangles are similar so
their sides are the same rapport
48/6=x/5
scale factor is 48/6=8
value of x ,we can use the formula
48/6=x/5
8=x/5
x=8*5=40
Anyone understand this ?? Please help, I literally dont understand math at all.

Answers
Answer:
A
Step-by-step explanation:
The entire frame is 42 x 23 in, but for each dimension there are two lengths of x inches that are included in the entire dimension but not that of the actual picture. Thus, the correct equation is (42 - 2x)(23 - 2x) = 700 which is choice A.
Use isometric dot paper to sketch prism.
cube 3 units on each edge
Answers
The sketching a cube with 3 units on each edge on isometric drawing dot paper, follow these steps:
Start by drawing a horizontal line segment of 3 units on the isometric dot paper. This will serve as the base of the cube.
From each end of the base, draw two vertical lines upward, each measuring 3 units. These lines should be parallel to each other and perpendicular to the base.
Connect the corresponding ends of the vertical lines with a horizontal line segment, creating the top face of the cube. Ensure that this line segment is also 3 units long.
Connect the corresponding vertices of the base and top face with vertical lines, completing the visible edges of the cube. These lines should be parallel to each other and perpendicular to both the base and top face.
Finally, draw dashed lines to represent the hidden edges of the cube. These dashed lines connect the non-corresponding vertices of the base and top face.
By following these steps, you will have sketched a cube with 3 units on each edge on isometric dot paper. Isometric dot paper is specifically designed to assist in drawing three-dimensional objects, and the dots on the paper help maintain the correct proportions.
Therefore, it is important to align the lines and vertices properly to ensure an accurate representation of the cube.
Learn more about isometric drawing here:
https://brainly.com/question/27991212
#SPJ4

WILL MARK YOU BRAINLIEST

Answers
Answer:
i believ its b
Step-by-step explanation:
Answer:
(-1,-3)
Step-by-step explanation:
90 degree rotation = (x,y) —> (-y,x)
can someone help me? i'm confunsed and I don't know anything

Answers
Answer:
See Below
Step-by-step explanation:
ABCD primes all correspond to x and y values on the graph.
A=
B=
C=
D=
1) y- intercept
2) time of max height
3) time when balloon hits ground
4) x-intercept
5) max height
6) Initial height
So lets look at (0,A)
This would count as the y - intercept as well as the height they started throwing the balloons.
Soo....
A = y-intercept; Initial height
Now, (B,C)
This is the highest point on the graph, therefore it would be the max time and max height.
If we look at this as a person behind the line throwing the ballon, the y would be the height and the x would be the time
B = Time of max height
C=Max height
(D,0)
From the visual above, this point would be where the balloon hits the ground
From the visual in our head, x is time and y is height
Since d is the x, it is the time when the balloon hits the ground. And since
y =0, D is also the x intercept
D = x intercept, Time when balloon hits ground
Therefore,
A = y-intercept; Initial height
B = Time of max height
C=Max height
D = x intercept, Time when balloon hits ground
Hope this helps! =D
What is the value of z, rounded to the nearest tenth? use the law of sines to find the answer. 2.7 units 3.2 units 4.5 units 5.3 units
Answers
The triangle is a shape with 3 sides and angles. The value of z from the given figure to the nearest tenth is 3.2
Sine rule of triangleThe triangle is a shape with 3 sides and angles
From the given triangle, we will use the expression below to determine the value of z
2.6/sin51= z/sin76
simplify
z = 2.6sin76/sin51
z = 2.5227/0.7771
z = 3.246
Hence the value of z from the given figure to the nearest tenth is 3.2
Learn more on sine rule here: https://brainly.com/question/27174058
#SPJ4
