Complete the table: (Enter your answers as a whole dollar amount.) Units Unit Cost Dollar Cost Beg. Inventory Jan. 1 8 $ 6.00 A Apr. 11 24 $ 11.00 B May 17 30 $ 14.00 C Dec. 5 19 $ 16.00 D 21 units sold

The volume of the prisms are:

1. 432 yd³

2. 36in³

3. 252 m³

4. 240 ft³

5. 576 mm³

6. 144 cm³

7. 343 m³

8. 120 yd³

9. 150 in³

The formula for calculating the volume of a rectangular prism is expressed as;

V = lwh

such that;

Now, substitute the value for each of the prisms, we have;

1. Volume = 6 × 6 ×12

Multiply

Volume = 432 yd³

2. Volume = 2 ×9 × 2

Multiply

Volume = 36in³

3. Volume = 9 × 4 × 7

Multiply

Volume = 252 m³

4. Volume = 10 × 8 × 3

Multiply

Volume = 240 ft³

5. Volume = 4 × 12 × 12

Multiply the values

Volume = 576 mm³

6. Volume = 6 × 8 × 3

Volume = 144 cm³

7. Volume = 7 × 7 ×7

Volume = 343 m³

8. Volume = 8 × 3 × 5

Volume = 120 yd³

9. Volume = 5 × 6 × 5

Volume = 150 in³

Learn more about volume at: https://brainly.com/question/1972490

#SPJ1

Answer:

a=-50

Step-by-step explanation:

Answer: ok when it start

Step-by-step explanation:

Answer:

thx so much :)

Step-by-step explanation:

The expression is equivalent to the 360\(k^2\) - 48k

Given the Expression :
8k5∙9k−2(6k2)2

It means

(8k × 5) × 9k - 2(6k × 2) × 2

Now, Multiply the monomials

360\(k^2\) - 2(6k × 2) × 2

Again, Multiply the monomials,

= 360\(k^2\) - 48k

Hence, The expression is equivalent to the 360\(k^2\) - 48k

What is Monomial ?

A monomial is a polynomial, which has only one term. A monomial is an algebraic expression with an single term but can have multiple variable and a higher degree too.

Learn more about  Algebraic Expression at:

https://brainly.com/question/2761247

#SPJ1

Answer:

  the distance from the center to the line is about 5.65, too far from a circle of radius 5.

Step-by-step explanation:

We can prove this by looking at the distance from the center of the circle to the line.

The distance from point (x, y) to line ax+by+c=0 is given by ...

  d = |ax +by +c|/√(a^2 +b^2)

For the line ...

  x -y -6 = 0

and the point (2, 4), the distance is ...

  d = |2 -4 -6|/(1^2 +(-1)^2) = |-8|/√2 = 8/√2 ≈ 5.65685

This tells us that a circle with radius 5.65 or less will not intersect the line. A circle of radius 5 is smaller than that. A circle with radius 5 will not intersect the line y = x-6.

The given expression is 4x + 2 + 7y. The true statements about this expression are:

An expression is formed by the terms connected with the arithmetic operations. Where the terms are formed by the coefficients and variables. A constant is also said to be a term in the expression.

Example: ax + by + c = 0; here there are 3 terms, ax, by and c, two variables x and y, and one constant c. The constant or numerals with the variables are said to be coefficients.

The given expression is 4x + 2 + 7y.

The expression has 3 terms. they are 4x, 2, 7y.

There are two variables x and y.

The coefficients for these variables are 4 and 7 respectively.

The numeral 2 is a constant in the given expression.

So, statements 1, 3, and 4 are true.

Learn more about expressions here:

https://brainly.com/question/4344214

#SPJ1

Answer:

( 0 , 1 ) ,  ( 1 , 0 )

( − 5 , 9 ) ,  ( 3 , 0 )

( 0 , 9 ) ,  ( 8 , 6 )

Step-by-step explanation:

V is a vector space with the operations of addition and scalar multiplication.

Since f(t) and g(t) are real numbers, you're utilizing the fact that the real numbers themselves are commutative in that step, which truly confused me when I first learned about it and after.

Let V denote the set of all differentiable real-valued functions defined on the real line.

You only need to mention that real-number addition is commutative. Since f is not a number until you evaluate, you couldn't do it before you did.

On a different note, you cannot say that

f+g=f(t)+g(t)

but you can say that (f+g)(t)=f(t)+g(t)

So  V is a vector space with the operations of addition and scalar multiplication.

Know more about scalar multiplication

https://brainly.com/question/26649852

#SPJ4

Answer:

386.75

Step-by-step explanation:

added in the picture

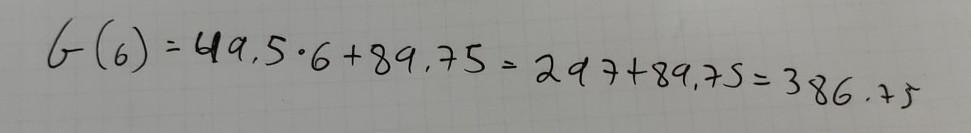
The cost of joining the gym for 6 months is 386.75.

Given,

The function G(m) = 49.5m + 89.75 represents the cost of joining the gym in addition to the one-time membership fee.

The cost, G, is measured in dollars for m months.

We need to find the value of G(6).​

Here,

The one-time membership = 89.75.

Now,

Putting m = 6 months in:

G(m) = 49.5m + 89.75

G(6) = 49.5 x 6 + 89.75

       = 297 + 89.75

       = 386.75

Thus the cost of joining the gym for 6 months is G(6) = 386.75.

Learn more about finding the value of a function here:

https://brainly.com/question/8822000

#SPJ2

Answer:

.8 equals 80%

Step-by-step explanation:

To find the percentage you multiply the decimal by 100 so .8 multiplyed by 100 equals 80 or 80%

Answer:

1/6 cup

Step-by-step explanation:

1/2 - 1/3 = 3/6 - 2/6 = 1/6 cup

Answer:

1. 12 days

2. more than 200 miles

3. 11 lawns

4. at least 9 hours (about 9.92 hours)

Step-by-step explanation:

1. 20x < 254, so x < 12.7. We need an integer here, so x = 12 days.

2.

\(70 + .15x < 50 + .25x\)

\(20 < .10x\)

\(200 < x\)

\(x > 200\)

3. 65x > 699, so x > 10.8. Since fractions of lawns are not accepted here, Mark must mow at least 11 lawns.

4. Assuming that the speed stays constant, 65x = 645, so x = 9.92 hours. The trip will take at least 9 hours, actually close to 10 hours.

The unit of the rate of change is (b) dollars per month

From the question, we have the following parameters that can be used in our computation:

The table of values

Where we have

y = total amount in dollars

x = number of months

The rate of change is calculated as

Rate  = y/x

substitute the known values in the above equation, so, we have the following representation

Rate = total amount in dollars/number of months

So, we have

Unit = dollars per month

Read more about rate of change at

https://brainly.com/question/31965106

#SPJ1

A psychologist selects a random sample of 25 handicapped students and measures their manual dexterity scores, then if she wants to improve her precision she should use a larger sample size.  

Each sample has an equal chance of being chosen as part of the sampling procedure known as random sampling. A randomly selected sample is intended to be a fair reflection of the entire population. By increasing sample size, you can improve the accuracy of your estimates, which means that the result will be more "statistically significant" for any given estimate or size of effect. The accuracy of the average results will increase with sample quantity. Smaller error margins and the identification of outliers in the data are two further benefits of larger sample sizes.

If they observe an effect that is almost significant, some researchers decide to increase their sample size. This is done rather than concluding that there is no effect because the researcher believes he is short on samples. Because the standard error is reduced as sample size increases, confidence intervals are narrower. c) The statement "there is a 95% likelihood that the population mean is between 350 and 400" is similar to the statement "there is a 95% confidence interval for the population mean is (350, 400)".

Learn more about random sample visit : brainly.com/question/24466382

#SPJ4

Correct Question:

A psychologist selects a random sample of 25 handicapped students and measures their manual dexterity scores. she uses this data to test the hypothesis that the mean dexterity score is different than 45. What would you advise her?

Answer:

8c

f(g(x)) = x^4 + 2x^3 - x

g(f(x)) =  x^4 + 2x^3 + 2x^2 - x

Step-by-step explanation:

f(x) = x^2 - x ; g(x) = x^2 + x

f(g(x)) = (x^2 + x)^2 - (x^2 + x)

f(g(x)) = (x^2 + x)^2 - x^2 - x

f(g(x)) = (x^2 + x)(x^2 + x) - x^2 - x

f(g(x)) = x^4 + x^3 + x^3 + x^2 - x^2 - x

f(g(x)) = x^4 + 2x^3 - x

g(f(x)) = (x^2 - x)^2 + x^2 - x

g(f(x)) = (x^2 + x)(x^2 + x) + x^2 - x

g(f(x)) = x^4 + x^3 + x^3 + x^2 + x^2 - x

g(f(x)) =  x^4 + 2x^3 + 2x^2 - x

Answer:

1/6 that's the answer

Step-by-step explanation:

so you do 43/6-7=43/6-42/6=1/6

Answer:

Actually the answer is -⅙

Step-by-step explanation:

43/6 written differently is 7 ⅙, because the fraction 42/6 is the same as 7 (42÷6=7). But since your number is 43/6 you get

7 1/6.

your original number is larger than 7 but the question was what number you have to "add" to get to 7. so they number has to be a negative number.

like this:

43/6 + (-1/6) = 42/6. which you rewrite now as

43/6 - 1/6 = 42/6. and I explained that 42/6 is the same as 7.

Answer:

inches

Step-by-step explanation:

well depends on how big your foot is

The length of line segment AB is 5 units.To find the length of line segment AB, we can use the distance formula, which is based on the Pythagorean theorem.

The distance formula calculates the distance between two points (x1, y1) and (x2, y2) in a coordinate plane.

Let's calculate the length of AB using the given coordinates for points A and B:

Coordinates of point A: A = (4, -5)

Coordinates of point B: B = (7, -9)

The distance formula is given by:

\(d = [(x2 - x1)^2 + (y2 - y1)^2]\)

Substituting the coordinates of A and B into the formula:

\(d = [(7 - 4)^2 + (-9 - (-5))^2]\\d =[(3)^2 + (-4)^2]\)

d = √[9 + 16]

d = √25

d = 5

Therefore, the length of line segment AB is 5 units.

The distance formula calculates the straight-line distance between two points in a two-dimensional space. In this case, it determines the distance between points A and B in the coordinate plane. By applying the formula and substituting the given coordinates, we find that the length of AB is 5 units.

For more such questions on distance formula.

https://brainly.com/question/661229

#SPJ8

Answer: 112 people.

Step-by-step explanation:

Answer:

You would need 112.5 people to eat all the stacks of pancakes.

Step-by-step explanation:

45 times 5 = 225

and then 225 divided by 2 is 112.5

Hope this helps!

Good question lol

Answer:

The answer is 16pi or 50.3cm² to 1 d.p

Step-by-step explanation:

The non shaded=area of shaded

d=8

r=d/2=4

A=pir³

A=p1×4²

A=pi×16

A=16picm² or 50.3cm² to 1d.p

Answer:

3.45 cm (3 s.f.)

Step-by-step explanation:

We have been given a 5-sided regular polygon inside a circumcircle. A circumcircle is a circle that passes through all the vertices of a given polygon. Therefore, the radius of the circumcircle is also the radius of the polygon.

To find the radius of a regular polygon given its side length, we can use this formula:

\(\boxed{\begin{minipage}{6 cm}\underline{Radius of a regular polygon}\\\\$r=\dfrac{s}{2\sin\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $r$ is the radius.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\\end{minipage}}\)

Substitute the given side length, s = 8 cm, and the number of sides of the polygon, n = 5, into the radius formula to find an expression for the radius of the polygon (and circumcircle):

\(\begin{aligned}\implies r&=\dfrac{8}{2\sin\left(\dfrac{180^{\circ}}{5}\right)}\\\\ &=\dfrac{4}{\sin\left(36^{\circ}\right)}\\\\ \end{aligned}\)

The formulas for the area of a regular polygon and the area of a circle given their radii are:

\(\boxed{\begin{minipage}{6 cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{nr^2\sin\left(\dfrac{360^{\circ}}{n}\right)}{2}$\\\\\\where:\\\phantom{ww}$\bullet$ $A$ is the area.\\\phantom{ww}$\bullet$ $r$ is the radius.\\ \phantom{ww}$\bullet$ $n$ is the number of sides.\\\end{minipage}}\)

\(\boxed{\begin{minipage}{6 cm}\underline{Area of a circle}\\\\$A=\pi r^2$\\\\where:\\\phantom{ww}$\bullet$ $A$ is the area.\\\phantom{ww}$\bullet$ $r$ is the radius.\\\end{minipage}}\)

Therefore, the area of the regular pentagon is:

\(\begin{aligned}\textsf{Area of polygon}&=\dfrac{5 \cdot \left(\dfrac{4}{\sin\left(36^{\circ}\right)}\right)^2\sin\left(\dfrac{360^{\circ}}{5}\right)}{2}\\\\&=\dfrac{5 \cdot \left(\dfrac{4}{\sin\left(36^{\circ}\right)}\right)^2\sin\left(72^{\circ}\right)}{2}\\\\&=\dfrac{\dfrac{80\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}}{2}\\\\&=\dfrac{40\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}\\\\&=110.110553...\; \sf cm^2\end{aligned}\)

The area of the circumcircle is:

\(\begin{aligned}\textsf{Area of circumcircle}&=\pi \left(\dfrac{4}{\sin\left(36^{\circ}\right)}\right)^2\\\\&=\dfrac{16\pi}{\sin^2\left(36^{\circ}\right)}\\\\&=145.489779...\; \sf cm^2\end{aligned}\)

The area of the shaded area is the area of the circumcircle less the area of the regular pentagon plus the area of the small central circle.

The area of the unshaded area is the area of the regular pentagon less the area of the small central circle.

Given the shaded area is equal to the unshaded area:

\(\begin{aligned}\textsf{Shaded area}&=\textsf{Unshaded area}\\\\\sf Area_{circumcircle}-Area_{polygon}+Area_{circle}&=\sf Area_{polygon}-Area_{circle}\\\\\sf 2\cdot Area_{circle}&=\sf 2\cdot Area_{polygon}-Area_{circumcircle}\\\\2\pi r^2&=2 \cdot \dfrac{40\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}-\dfrac{16\pi}{\sin^2\left(36^{\circ}\right)}\\\\2\pi r^2&=\dfrac{80\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}-\dfrac{16\pi}{\sin^2\left(36^{\circ}\right)}\\\\\end{aligned}\)

                                                 \(\begin{aligned}2\pi r^2&=\dfrac{80\sin\left(72^{\circ}\right)-16\pi}{\sin^2\left(36^{\circ}\right)}\\\\r^2&=\dfrac{40\sin\left(72^{\circ}\right)-8\pi}{\pi \sin^2\left(36^{\circ}\right)}\\\\r&=\sqrt{\dfrac{40\sin\left(72^{\circ}\right)-8\pi}{\pi \sin^2\left(36^{\circ}\right)}}\\\\r&=3.44874763...\sf cm\end{aligned}\)

Therefore, the radius of the small circle is 3.45 cm (3 s.f.).

Answer:

y=2/9x+2

Step-by-step explanation:

Answer:

y = \(\frac{2}{9}\) x + 2

Step-by-step explanation:

Slope intersept form is y = mx +b

Y-intersept (b) is 2

Slope (m) is \(\frac{2}{9}\)

Plug the slope(m) and Y-intersept (b) into y = mx +b : y = \(\frac{2}{9}\) x + 2

The value that is not reasonable for the true mean weight of the residents of the town is 193 pounds

Given that the mean weight is 187 pounds with a margin of error of 3 pounds, we can construct the interval as follows:

Mean weight - Margin of error = 187 - 3 = 184 pounds

Mean weight + Margin of error = 187 + 3 = 190 pounds

So, the reasonable range for the true mean weight of the residents of the town is between 184 and 190 pounds.

Now, let's evaluate the options to identify the value that falls outside this reasonable range:

A. 170 pounds - This value falls below the lower limit of the reasonable range (184 pounds). Therefore, it is not a reasonable value for the true mean weight.

B. 188 pounds - This value falls within the reasonable range of 184 to 190 pounds. It is a reasonable value.

C. 193 pounds - This value falls above the upper limit of the reasonable range (190 pounds). Therefore, it is not a reasonable value for the true mean weight.

D. 186 pounds - This value falls within the reasonable range of 184 to 190 pounds. It is a reasonable value.

E. 182 pounds - This value falls below the lower limit of the reasonable range (184 pounds). Therefore, it is not a reasonable value for the true mean weight.

From the options provided, the value that is not reasonable for the true mean weight of the residents of the town is 193 pounds.

Learn more about Margin of Error here:

https://brainly.com/question/16981466

#SPJ1

For the given function the intercepts are:

x-intercept: x = -4

y-intercept: y = 12.

Here we have a table that defines a function, and we want to find the intercepts of said function.

We can assume it is linear, then the slope of the function will be given by:

a = (9 - 3)/(-1 + 3) = 6/2 = 3

The linear function is like:

y = 3x + b

To find the value of b we can replace the values of the last point on the table, x = 2 and y = 18.

18 = 3*2 + b

18 = 6 + b

18 - 6 = b = 12

The linear function is:

y = 3x + 12

The x-intercept is the value of x when y = 0

0 = 3*x + 12

-12 = 3x

-12/3 = x = -4

And the y-intercept is the value of y when x = 0.

y = 3*0 + 12

y = 12

Learn more about intercepts at:

https://brainly.com/question/1884491

#SPJ1

From the statement of the problem, we know that:

• Thomas has 40 cups of flour,

• he wants to share equally with 5 friends.

If Thomas wants to share equally the cups of flour with his friends, he must give the same number of cups to each friend, that number is given by the quotient:

So each friend will receive 8 cups of flour. Now, because each cup has 4 quarts, each friend will receive:

Answer

Each friend will receive 32 quarts of flour.

Answer:

48.43552415324934

Step-by-step explanation:

61.73²-38.27² = 2346

\(\sqrt{2346}\) = 48.43552415324934

It will cost approximately $2940 to cover the circular region with mud.

The term "cost" in mathematics usually refers to the sum of money or resources needed to acquire or manufacture something.

It can be quantified as a number, frequently in a particular currency.

The formula C = 2r, where r is the circle's radius, determines the circumference of a circle.

In this case, we know that the circumference is about 157 feet, so we can set up an equation:

157 = 2πr

Solving for r, we get:

r = 157 / (2π) ≈ 25

So the radius of the circular region is approximately 25 feet.

The equation A = r² determines a circle's surface area.

Using the radius we just found, we can calculate the area:

A = π(25)² ≈ 1963.5 square feet

The cost to cover 1 square foot with mud is $1.50, so the cost to cover the entire area with mud is:

1963.5 × $1.50 = $2945.25

Rounding to the nearest ten dollars, the cost is:

$2940

To know  more about area visit:

https://brainly.com/question/13135497

#SPJ1