Answers
Answer:
To find all the equivalent expressions to the given expression, we can simplify it step by step using the properties of exponents:
(18^5)^3/8
Step 1: Simplify the exponent inside the parentheses:
18^(5*3)/8
18^15/8
Step 2: Rewrite the exponent as a product of two exponents:
(18^15)^(1/8)
Step 3: Apply the property of taking the exponent of an exponent:
18^(15*(1/8))
Step 4: Simplify the exponent:
18^(15/8)
Therefore, the equivalent expressions to (18^5)^3/8 are:
(18^15)^(1/8)
18^(15*(1/8))
18^(15/8)
Step-by-step explanation:
Answer:
1,3,5 is the answer (灬º‿º灬)♡
Related Questions
Please help me! (Tangent Ratios) (20 points)
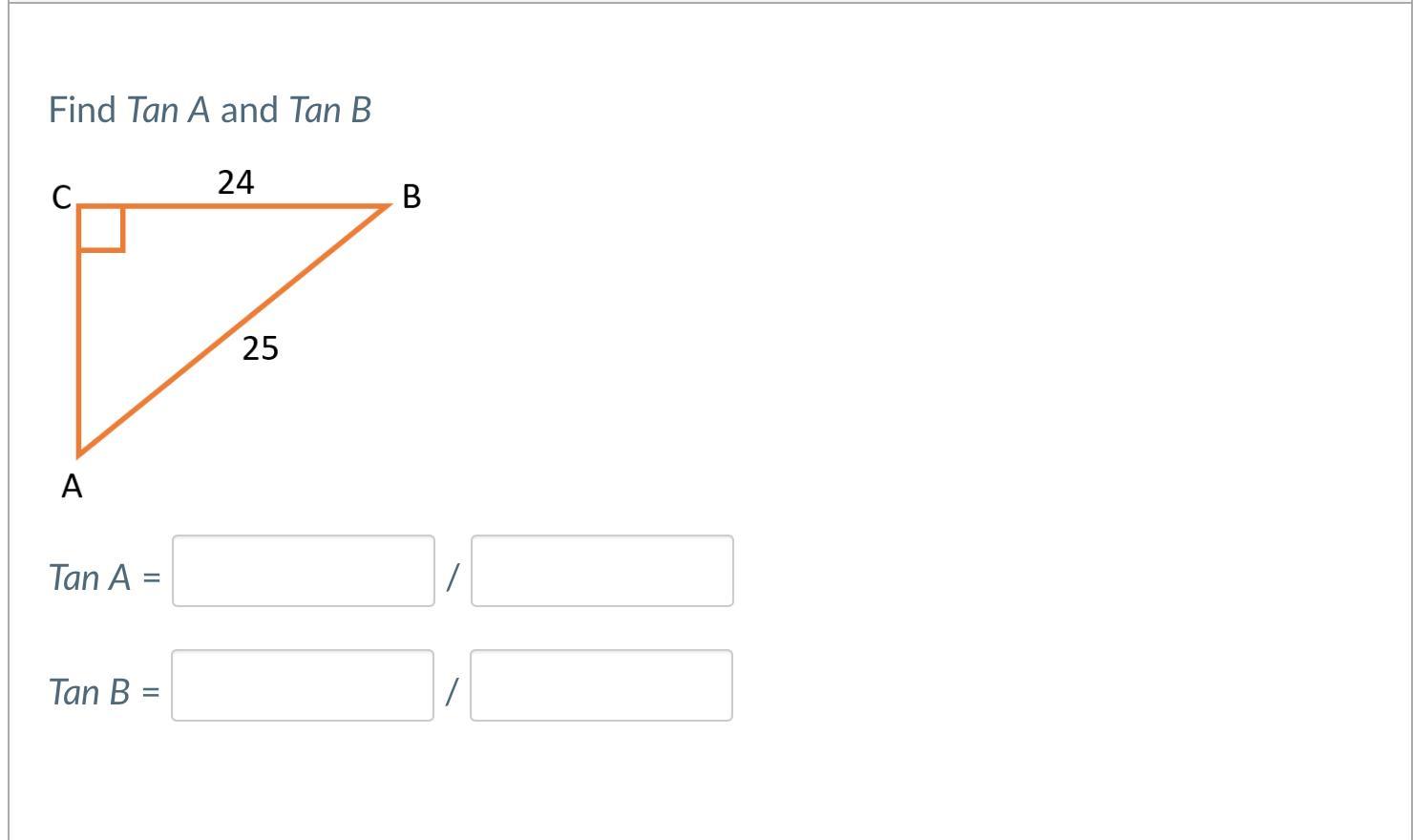

Answers
Answer:
Tan A for first page 25/49
Tan A for second page 37/49
Tan B for first page 24/49
Tan B for second page 12/49
guys can anyone help me with my other SAT question"
The owner of the Good Deals Store opens a new store across town. For the new store, the owner estimates that, during business hours, an average of 90 shoppers per hour enter the store and each of them stays an average of 12 minutes. The average number of shoppers in the new store at any time is what percent less than the average number of shoppers in the original store at any time? (Note: Ignore the percent symbol when entering your answer. For example, if the answer is 42.1%, enter 42.1)
Answers
Answer: To solve this problem, we need to first find the average number of shoppers in the new store at any time and the average number of shoppers in the original store at any time, and then calculate the percent difference between the two.
Let's start by finding the average number of shoppers in the new store at any time. We know that 90 shoppers enter the store per hour, and each shopper stays for an average of 12 minutes, which is 0.2 hours. So the number of shoppers in the store at any time is:
90 shoppers/hour × 0.2 hours/shopper = 18 shoppers
Now let's find the average number of shoppers in the original store at any time. We don't have any information about the original store, so let's call the average number of shoppers in the original store "x". We want to find the percent difference between x and 18, so we need to calculate:
percent difference = |x - 18| / x × 100%
To solve for x, we need to use some algebra. We know that the number of shoppers entering the original store per hour is equal to the number of shoppers leaving the store per hour (assuming the store has a steady flow of shoppers and no one stays for more than an hour). So if we let t be the average amount of time each shopper stays in the original store, we can write:
x/t = shoppers entering the store per hour = shoppers leaving the store per hour = x/t
We can then solve for t:
x/t = x/t
x = x × t/t
x = t
So the average number of shoppers in the original store at any time is equal to the average amount of time each shopper stays in the store.
We don't know the average amount of time each shopper stays in the original store, but we can make an estimate based on the information we have about the new store. We know that the average amount of time each shopper stays in the new store is 12 minutes, or 0.2 hours. If we assume that the shopping behavior is similar in both stores, we can use this estimate for the original store as well.
So we have:
x = t = 0.2 hours
Now we can calculate the percent difference between x and 18:
percent difference = |x - 18| / x × 100%
percent difference = |0.2 - 18| / 0.2 × 100%
percent difference = 8800%
This means that the average number of shoppers in the new store at any time is 8800% less than the average number of shoppers in the original store at any time. However, this answer seems implausible, since a percent difference greater than 100% means that the new store has a negative number of shoppers!
It's possible that there was an error in the problem statement, such as a typo or a missing decimal point. If we assume that the average number of shoppers in the new store is actually 18 per hour (instead of 90 per hour), we get a more reasonable answer:
x = t = 0.2 hours
percent difference = |x - 18| / x × 100%
percent difference = |0.2 - 18| / 0.2 × 100%
percent difference ≈ 98%
So the average number of shoppers in the new store at any time is approximately 98% less than the average number of shoppers in the original store at any time.
Step-by-step explanation:
Consider this graph of a line.

Answers
The linear equation of the line shown in the graph will be 3y +x= 0.
What is the Linear equation?A linear equation is an algebraic equation of the form y=mx+b, where m is the slope and b is the y-intercept, and only a constant and a first-order (linear) term are included. Sometimes, the aforementioned is referred to as a "linear equation of two variables," with y and x serving as the variables.
As we can observe in the given graph of lines,
the given line passes through the point (0, 0) origin and (-6, 2).
The slope-intercept form of the equation of a line
y=mx+b,
where m is the slope
b is the y-intercept
Since y-intercept is the value of y in line at x = 0
in our case, b = 0
since, slope = (y - y')/(x -x')
Slope = (2-0)/(-6-0)
Slope = 2/-6
Slope = -1/3
thus,
the equation of the line shown in the graph will be y = -1/3x
the equation of the line shown in the graph will be 3y +x= 0.
Learn more about Linear equations here:
https://brainly.com/question/11897796
#SPJ9
Question 5 Use the rules of differentiation to find the derivative of the function y (6x + 1)5 + 30x(6x + 1)ª (6x + 1)² (36x + 1) 1 X 6 No correct answer provided. = X x(6x + 1)5.
Answers
The derivative of the function y = x(6x + 1)⁵ is: dy/dx = (6x + 1)⁵ + 30x(6x + 1)⁴
To find the derivative of the given function, we can apply the rules of differentiation. Using the product rule, we differentiate each term separately and then add them together.
For the first term x, the derivative is simply 1.
For the second term (6x + 1)⁵, we apply the chain rule. The derivative of (6x + 1)⁵ with respect to x is 5(6x + 1)⁴ multiplied by the derivative of the inner function 6x + 1, which is 6.
Multiplying these derivatives together, we get (6x + 1)⁵ * 6 = 6(6x + 1)⁵.
For the third term x(6x + 1)⁴, we again apply the product rule. The derivative of x is 1, and the derivative of (6x + 1)⁴ is 4(6x + 1)³ multiplied by the derivative of the inner function 6x + 1, which is 6.
Multiplying these derivatives together, we get x * 4(6x + 1)³ * 6 = 24x(6x + 1)³.
Finally, we add the derivatives of each term to get the derivative of the entire function: dy/dx = (6x + 1)⁵ + 30x(6x + 1)⁴.
To know more about derivative, refer here:
https://brainly.com/question/2159625#
#SPJ11
Complete question:
Use the rules of differentiation to find the derivative of the function y= x(6x + 1)⁵
(6x + 1)⁵ + 30x(6x + 1)⁴
(6x + 1)⁴ (36x + 1)
x-1/6
No correct answer provided.
There are approximately, 18 men for 2 women in the armed forces. In a group of 90 military personnel, how many would you expect to be women?
Answers
Answer: 10 women
Step-by-step explanation:
From the question, we are informed that there are 18 men for 2 women in the armed forces. This gives us a fraction of: 2/18 = 1/9
In a group of 90 military personnel, the number that'll be expected to be women will be:
= 1/9 × 90
= 10 women
Consider the logistic differential equation:
dy/dx = y/8(6 - y)
Let f(t) be the particular solution to the differential equationwith f(0) = 8
a. What is the limiting factor?
b. Use Euler's method, starting at t=0 with two steps of equalsize, to appropriate F(1).
c. What is the range of f for t > 0
Answers
The approximate value of f(1) using Euler's method with two steps of equal size is 6.636. The range of f for t > 0 is 0 < f(t) < 6.
a. The limiting factor in this logistic differential equation is the carrying capacity, which is 6 in this case. As y approaches 6, the growth rate of y slows down, until it eventually levels off at the carrying capacity.
b. To use Euler's method, we first need to calculate the slope of the solution at t=0. Using the given differential equation, we can find that the slope at t=0 is y(0)/8(6-y(0)) = 8/8(6-8) = -1/6.
Using Euler's method with two steps of equal size, we can approximate f(1) as follows:
f(0.5) = f(0) + (1/2)dy/dx|t=0
= 8 - (1/2)(1/6)*8
= 7.333...
f(1) = f(0.5) + (1/2)dy/dx|t=0.5
= 7.333... - (1/2)(7.333.../8)*(6-7.333...)
= 6.636...
Therefore, the approximate value of f(1) using Euler's method with two steps of equal size is 6.636.
c. The range of f for t > 0 is 0 < f(t) < 6, since the carrying capacity of the logistic equation is 6. As t approaches infinity, f(t) will approach 6, but never exceed it. Additionally, f(t) will never be negative, since it represents a population size. Therefore, the range of f for t > 0 is 0 < f(t) < 6.
Learn more about Euler's method here
https://brainly.com/question/21245378
#SPJ11
The area of the rectangle ABCD is 28\(cm^{2}\)
a) What is the length of side AB in terms of x?
length of AB = (Answer here) (1)
b) If the area of rectangle ABCD is 28\(cm^{2}\), we can show that \(x^{2}\) + ax = b where a and b are integer values.
Work out the values of a and b.
a = (Answer here) (1) b = (Answer here) (1)
![The area of the rectangle ABCD is 28[tex]cm^{2}[/tex]a) What is the length of side AB in terms of x?length](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/HzDUEA3Mp20S2mqrTmau3qyfeVRzJkuW.png)
Answers
Answer:
see explanation
Step-by-step explanation:
(a)
AB = 4 + x
(b)
the area (A) of rectangle ABCD is calculated as
A = length × breadth
= AB × AD
= (4 + x)(6 + x) ← expand using FOIL
= 24 + 10x + x²
given A = 28 , then
x² + 10x + 24 = 28 ( subtract 24 from both sides )
x² + 10x = 4 ← in the form x² + ax = b
with a = 10 and b = 4
Susanna purchased a shirt for $5 pants for $10 and a jacket for $25 she wants to buy at least one purse for the outfit but she wants to have something left of her original $65 how much money might she spend on the purse?
Answers
Answer:
Spends $20 and she has $5 leftover.
Step-by-step explanation:
I'm having a hard time with this question so someone help please

Answers
Answer:
7.7 km
Step-by-step explanation:
This question is asking you to find the third side of a triangle in which two sides and an angle not between them are given. The law of sines provides the necessary relationships.
Law of SinesThe Law of Sines tells you that triangle side lengths are proportional to the sine of the opposite angle. For this triangle TPJ, the relation is ...
t/sin(T) = p/sin(P) = j/sin(J)
We are given T=68°, p=5.2 km, t=7.5 km, and we are asked to find the length of j, the TP distance.
SetupWe know the sum of angles in a triangle is 180°, and the sine of an angle is equal to the sine of its supplement. This lets us fill in the Law of Sines equation like this:
7.5/sin(68°) = 5.2/sin(P) = j/sin(68°+P) . . . . . solve for j
SolutionThis can be solved in two steps. First, we find angle P, then we use that to find length j.
sin(P) = 5.2/7.5 × sin(68°) ≈ 0.642847
P = arcsin(0.642847) ≈ 40.0045°
Now, we can find j:
j = 7.5 × sin(68° +40.0045°)/sin(68°) ≈ 7.693 . . . km
The distance from the tower to the plane is about 7.7 km.
__
Additional comment
We have used T, P, and J to refer to the vertices at the tower, plane, and jet.
The triangle can also be solved using the Law of Cosines. In that case, the missing side will be the solution to a quadratic equation with irrational coefficients.
write the fraction in 2 different ways

Answers
Answer:
a. \(\frac{3}{5} = \frac{1}{5} + \frac{1}{5} + \frac{1}{5}\)
b. \(\frac{3}{5} = \frac{2}{5} + \frac{1}{5}\)
I hope this helps!
Step-by-step explanation:
3/5=1/5+1/5+1/5
3/5=2/5+1/5
A line L is parallel to the line 2x-5y-8=0. What is the gradient of the line
Answers
Answer:
2/5
Step-by-step explanation:
1) rearrange the equation in the form y=mx+c where m is the gradient and y is the y intercept
2x-5y-8=0
add 5y to both sides
2x-8=5y
divide 5 on both sides
2/5x - 8/5 = y
overall equation is y=2/5x-8/5
the gradient is 2/5
sketch the region enclosed by the given curves. y = cos(x), y = sin(2x), 0 ≤ x ≤ 2
Answers
To sketch the region enclosed by the curves y = cos(x) and y = sin(2x) for the interval 0 ≤ x ≤ 2, we can follow these steps:
1. Plot the graphs of the two functions separately on the given interval.
For y = cos(x):
- Start by marking key points on the graph: (0, 1), (π/2, 0), (π, -1), (3π/2, 0), (2π, 1).
- Connect the points smoothly to create a curve that oscillates between 1 and -1.
For y = sin(2x):
- Start by marking key points on the graph: (0, 0), (π/4, 1), (π/2, 0), (3π/4, -1), (π, 0), (5π/4, 1), (3π/2, 0), (7π/4, -1), (2π, 0).
- Connect the points smoothly to create a curve that oscillates between 1 and -1, but with twice the frequency of the cosine curve.
2. Identify the region enclosed by the curves.
- The region enclosed by the curves is the area between the two curves from x = 0 to x = 2.
3. Shade the region enclosed by the curves.
- Shade the area between the two curves on the interval 0 ≤ x ≤ 2.
To know more about curve region refer here:
https://brainly.com/question/14390012?#
#SPJ11
someone, please help me out with these two problems, it's trig.

Answers
Answer:
2nd problem
The sum of the angles of the triangle is 180°.
B= 90°
Write an equation of the line through (2,5) and parallel to y = 3x - 8. Write the equation in the form x = a, y=b, or y=mx+b.
The equation of the line is
d
>

Answers
Answer:
thats a really hard question problem is that my phones broken and i cant see clearly
Step-by-step explanation:
Answer:
10
Step-by-step explanation:
Brainlyyyyyyyy
can somebody please answer this ? Will mark brainliest if you hurry

Answers
Answer:
83 calories
Step-by-step explanation:
Answer:
553 calories
Step-by-step explanation:
He will burn 420 for running because 1,080/2.5 = 420. He will burn 133 because 266 times 0.5 equals 133. So a total of 553 when you add the two.
Two families visited an amusement park. the first family bought 2 hot dogs and 3 bottles of waters, which totaled $18. the second family bought 4 hot dogs and 2 bottles of waters, which totaled $28. how much did one hot dog cost? a. $2 b. $4c. $5 d. $6
Answers
Answer:
d. $6
Step-by-step explanation:
2x + 5y = 14 4x + 2y = -4 solving with elimination
Answers
Answer:
(- 3, 4 )
Step-by-step explanation:
2x + 5y = 14 → (1)
4x + 2y = - 4 → (2)
multiplying (1) by - 2 and adding to (2) will eliminate the x- term
- 4x - 10y = - 28 → (3)
add (2) and (3) term by term to eliminate x
0 - 8y = - 32
- 8y = - 32 ( divide both sides by - 8 )
y = 4
substitute y = 4 into either of the 2 equations and solve for x
substituting into (1)
2x + 5(4) = 14
2x + 20 = 14 ( subtract 20 from both sides )
2x = - 6 ( divide both sides by 2 )
x = - 3
solution is (- 3, 4 )
melissa buys 212 pounds of salmon and 114 pounds of trout. she pays a total of $31.25, and the trout costs $0.20 per pound less than the salmon. what would be the combined cost of 1 pound of salmon and 1 pound of trout?
A. $15.60
B. $15.80
C. $16.60
D. $16.80
Answers
It is not possible to determine the combined cost of 1 pound of salmon and 1 pound of trout based on the given information.
To find the combined cost of 1 pound of salmon and 1 pound of trout, we need to determine the individual costs of each type of fish and then add them together.
Let's denote the cost of 1 pound of salmon as "s" and the cost of 1 pound of trout as "t". We know that Melissa buys 212 pounds of salmon and 114 pounds of trout, and she pays a total of $31.25.
From the given information, we can set up two equations:
Equation 1: 212s + 114t = 31.25 (total cost equation)
Equation 2: t = s - 0.20 (trout costs $0.20 per pound less than salmon)
To find the combined cost, we need to eliminate one variable. Let's solve Equation 2 for s:
s = t + 0.20
Substituting this value of s in Equation 1, we get:
212(t + 0.20) + 114t = 31.25
Expanding and simplifying the equation:
212t + 42.40 + 114t = 31.25
326t + 42.40 = 31.25
326t = 31.25 - 42.40
326t = -11.15
t = -11.15 / 326
t ≈ -0.034
However, since we're dealing with the cost of fish, a negative value doesn't make sense. So, we can conclude that there may be an error in the given information or calculation.
Learn more about pound from the given link:
https://brainly.com/question/498964
#SPJ11
plsss help (on pic)
First will put brainliest

Answers
Answer:
7 over 2x-2
Step-by-step explanation:
Answer:
g^-1 •7
7g^-1
7•1/g
answer is 7/g
I hoped I helped!! :)
The figure shows some cubes of edges 1 centimetre stacked in a corner. How many 1 cm cubes must be added to form a cube with each edge measuring 5 centimetres?

Answers
Answer: I think If a cube has an edge length of 1 cm, and it is divided into 5 cm cubes, there will be 1 x 1 x 1= 1 cm cube.
Please solve this as soon as possible

Answers
Answer:
Below in bold.
Step-by-step explanation:
The total sum of the numbers in A is 124 and the sum of the numbers in B = 56
Let x be the number passed from A to B, then from the given information:
124 - x = 56 + x + 20
124 - 56 - 20 = 2x
48 = 2x
x = 24.
a) So the number passed is 24.
b) Sum of numbers in B = 56 + 24 = 80.
c) Let pencil cost x then pen will cost 1.1 - x.
Now the pen costs 1 pound more than the pencil
so 1.1 - x - x = 1
-2x = -0.1
x = 0.05.
So the pen costs 1.1 - 0.05 = £1.05.
Evaluate the integral. Show that the substitution x = 4 sin(0) transforms / into / do, and evaluate I in terms of 0. Dx 1 / 7 = V16 - r? (Use symbolic notation and fractions where needed. Use C for the arbitrary constant. Absorb into C as much as possible. ) 1 = sin(0) + Incorrect
Answers
The integral solution is: ∫\((1/(7\sqrt{(16 - x^2)))} dx = (1/112) arcsin(x/4) + C.\)
To evaluate the integral ∫\((1/(7\sqrt{(16 - x^2)))} dx\) using the substitution x = 4 sin(θ), we can start by finding dx/dθ:
dx/dθ = 4 cos(θ)
∫\((1/(7\sqrt{(16 - x^2)))} dx\)= ∫\((1/(7\sqrt{(16 - 16sin^2}\)(θ)))) (\(4cos\)(θ)) dθ
Simplifying the denominator, we get:
∫\((1/(7\)\(\sqrt{(16 - 16sin^2}\)(θ)))) \((4cos\)(θ)) dθ = ∫\((1/(28cos\)(θ))) dθ
Now we can use the trigonometric identity cos^2(θ) = 1 - sin^2(θ) to rewrite the denominator:
∫\((1/(28cos\)(θ))) dθ = ∫\((1/(28\)√\((1 - sin^2\)(θ)))) dθ
dx = 4 cos(θ) dθ
∫\((1/(28√(1 - sin^2\)(θ)))) dθ = ∫\((1/(28√(1 - (x/4)^2))) (1/4) dx\)
This is the form of the integral that we can evaluate using the substitution \(u = x/4\) and the formula for the integral of \(1/\) √\((1 - u^2)\), which is arcsin(u) + C.
Substituting \(u = x/4\) and simplifying, we get:
\((1/112)∫(1/√(1 - (x/4)^2)) dx = (1/112) arcsin(x/4) + C\)
Therefore, the solution is:
\(∫(1/(7√(16 - x^2))) dx = (1/112) arcsin(x/4) + C\)
To learn more about integral visit:
https://brainly.com/question/31433890
#SPJ4
Several sources estimate that the average single family home in the United States uses about 420 pounds of copper within the plumbing, appliances, and building wires. In the 21st century, and average copper grade ore might be -0.6% copper. a) How many pounds of 0.6% grade copper ore needs to be mined in order to obtain 420 pounds of copper? Show your work. 2.52 pounds (420x0.6) = 252/100 = 2.52 pounds b) Tailings are the waste (ground rock and process effluent) left over from the mining process. The disposal of tailings is commonly identified as the single most important source of environmental impact from many mining operations. How much ground rock would be left to dispose of?
Answers
70,000 pounds of 0.6% grade copper ore needs to obtain 420 pounds of copper and 69,580 pounds of ground rock would be left after extracting 420 pounds of copper from the 0.6% grade copper ore.
How to find pounds of copper for different conditions?
0.6% copper in ore = 0.006 (as a decimal)
Let x be the pounds of copper ore needed to be mined.
So, the proportion is:
0.006x = 420
Now, we solve for x:
x = 420 / 0.006
x = 70,000 pounds
So, 70,000 pounds of 0.6% grade copper ore needs to be mined to obtain 420 pounds of copper.
To find out how much ground rock would be left to dispose of, we need to subtract the 420 pounds of copper from the total 70,000 pounds of copper ore.
Ground rock to dispose = Total copper ore - Copper obtained
Ground rock to dispose = 70,000 - 420
Ground rock to dispose = 69,580 pounds
Thus, 69,580 pounds of ground rock would be left to dispose of after extracting 420 pounds of copper from the 0.6% grade copper ore.
Learn more about ground rock
brainly.com/question/13314395
#SPJ11
what is the word used to describe a vector that always points toward the center of a circular path?
Answers
"Centripetal is the word used to describe a vector that always points toward the centre of a circular path."
The centripetal acceleration vector is an acceleration in the radial direction that is directed towards the centre of the circular line of motion. It runs perpendicular to the linear motion, or v.
The direction of the velocity shift for a ball travelling around a curve is in the direction of the curve's centre. Centripetal acceleration is the acceleration that is directed towards the centre of a curved or circular route.
Any force that changes the path of motion towards the centre of a circular motion is known as a centripetal force. The portion of the force that produces the centripetal force is the part that is perpendicular to the velocity.
To know more about vectors:
https://brainly.com/question/13590043
#SPJ4
what are the major methods of recording unstructured observational data
Answers
The major methods of recording unstructured observational data are Narrative Description, Field Notes, Audio or Video Recording, Photography, Diagrams or Maps.
The major methods of recording unstructured observational data are:
1. Narrative Description: This method involves writing a detailed, chronological account of the observed events or behaviors, capturing the context and interactions as they occur naturally.
2. Field Notes: In this method, the observer takes brief, concise notes during the observation, focusing on key events, behaviors, or interactions. These notes can be expanded and organized later for further analysis.
3. Audio or Video Recording: Using audio or video equipment, the observer captures the events and interactions in their entirety. This allows for a more accurate record and the ability to review and analyze the data multiple times.
4. Photography: Taking photographs during the observation can provide a visual record of the events and behaviors. These images can supplement other data collection methods and help to illustrate specific aspects of the observation.
5. Diagrams or Maps: Drawing diagrams or maps of the observation setting can help capture the spatial relationships between individuals and objects, as well as the overall layout of the environment.
These methods can be used individually or in combination, depending on the research question and the specific needs of the study. Remember to always respect participants' privacy and obtain informed consent when necessary.
To learn more about unstructured data
https://brainly.com/question/30977617
#SPJ11
A vase contains 60 marbles, all of which are red or orange. if the ratio of red marbles to orange ones is 1:5, what is the total number of red marbles in the vase?
Answers
The total number of red marbles in the vase are 10.
What is the ratio?A ratio is described as a comparison between two amounts with the same unit to determine the amount of 1 quantity is contained in the other. Ratios are divided into two sorts.
The first is a part-to-part ratio, and the second is a part-to-whole ratio. The part-to-part ratio expresses the relationship between 2 separate entities or groupings.
Now, according to the question;
Let 'x' be the red marbles in the vase.
Let 'y' be the orange marbles in the vase.
The total number of marbles in the vase are 60
x + y = 60 (equation 1)
The ratio of red marbles to orange ones is 1:5.
Thus, x/y = 1/5
cross multiplying;
5x = y
or y = 5x
substitute the value of y in equation 1;
x + y = 60 (equation 1)
x + 5x = 60
6x = 60
x = 10 (red marbles)
Thus, the number of red marbles in the vase are 10.
To know more about the ratio, here
https://brainly.com/question/25927869
#SPJ4
In a recent election, 63% of all registered voters participated in voting. In a survey of 275 retired voters, 162 participated in voting. Which is higher, the population proportion who participated or the sample proportion from this survey?
Answers
The population proportion who participated in voting (63%) is higher than the sample proportion from this survey (58.91%).
To determine whether the population proportion who participated in voting or the sample proportion from the survey is higher, we need to compare the percentages.
The population proportion who participated in voting is given as 63% of all registered voters.
This means that out of every 100 registered voters, 63 participated in voting.
In the survey of retired voters, 162 out of 275 participants voted. To calculate the sample proportion, we divide the number of retired voters who participated (162) by the total number of retired voters in the sample (275) and multiply by 100 to get a percentage.
Sample proportion = (162 / 275) \(\times\) 100 ≈ 58.91%, .
Comparing the population proportion (63%) with the sample proportion (58.91%), we can see that the population proportion who participated in voting (63%) is higher than the sample proportion from this survey (58.91%).
Therefore, based on the given data, the population proportion who participated in voting is higher than the sample proportion from this survey.
It's important to note that the sample proportion is an estimate based on the surveyed retired voters and may not perfectly represent the entire population of registered voters.
For similar question on population proportion.
https://brainly.com/question/29516589
#SPJ8
Using the graphing function on your calculator, find the solution to the system
of equations shown below.
OA. x= 13/12, y = -3/4
OB. More than 1 solution
C. x=-6, y = 2
D. No solution
4y + 12x = 10
2y-6x=-8
Answers
By using the graphing function on a calculator, a solution to the system of equations shown above include the following: A. x = 13/12, y = -3/4.
What is a graph?In Mathematics, a graph can be defined as a type of chart that is typically used to graphically represent data points or ordered pairs on both the horizontal and vertical lines of a cartesian coordinate, which are the x-axis (x-coordinate) and y-axis (y-coordinate) respectively.
In this scenario, we would use an online graphing calculator to plot the given system of equations and then take note of the point of intersection;
4y + 12x = 10 ........equation 1.
2y - 6x = -8 ........equation 2.
Based on the graph (see attachment), we can logically deduce that the solution to the given system of equations is the point of intersection of the lines on the graph representing each of them, which is given by the ordered pair (13/12, -3/4) or (1.083, -0.75).
Read more on a graph here: brainly.com/question/4546414
#SPJ1

What is the greatest possible error for a measurement of 0.05 metric tons?
Answers
Answer:The greatest possible error of a measurement is considered to be one-half of the measuring unit. If you measure a length to be 4.3 cm. (measuring to the nearest tenth), the greatest possible error is one-half of one tenth, or 0.05. This means that any measurements in the range from 4.25 cm. to 4.35 cm. are perceived as correct.
Step-by-step explanation:
Answer:
The greatest possible error for a measurement of 0.05 metric tons would depend on the accuracy of the measurement device or technique being used. Without more information about the specific measurement method, it is impossible to determine the greatest possible error.
Step-by-step explanation:
6.10.22 we are given n 1 numbers from the set {1, 2, . . . , 2n}. prove that there are two numbers among them such that one divides the other.
Answers
The two numbers among them are such that one divides the other.
The Collection of well-defined objects or elements is known as a set. The objects in a set are called elements. The Set contains a finite number of elements. The Set is denoted by any capital letter like A, B etc. Elements of the set can be numbers, alphabets etc.
The elements of the set are listed inside the curly brackets { ..... }. There are various types of sets. Cardinal number or cardinality denotes the number of elements in the set. Cardinality is denoted by n( X ) where X is a set. The number of subsets of the set is given by 2^n.
As per the question,
numbers = n + 1set = { 1, 2 . . . . . . . . . 2n }Let us divide the set into two sets,
A = { 1, 3 . . . . . n } and B = { 2, 4 . . . . . . 2n }
A and B contain the same number of elements i.e. two sets have equal sizes. Element of B is one of the elements of A multiplied by 2 or elements of B multiplied by 2. So, if we remove the powers of 2 i.e we divide each element by \(2^{k}\). Then there exist another 2 sets \(A ^{'}\) and \(B^{'}\) such that \(A ^{'}\) U \(B^{'}\) = \(A ^{'}\) .
By using the pigeonhole principle, \(A ^{'}\) consists of n elements and we add +1 to it additionally.
Therefore, When we are given n + 1 numbers from set { 1, 2 . . . . 2n }, there are two numbers among them such that one divides the other.
To know more about Sets refer to:
brainly.com/question/24700823
#SPJ4
