There exists exactly one line througn any two points. True or False
Answers
This statement is True due to the Two Point Postulate.
Related Questions
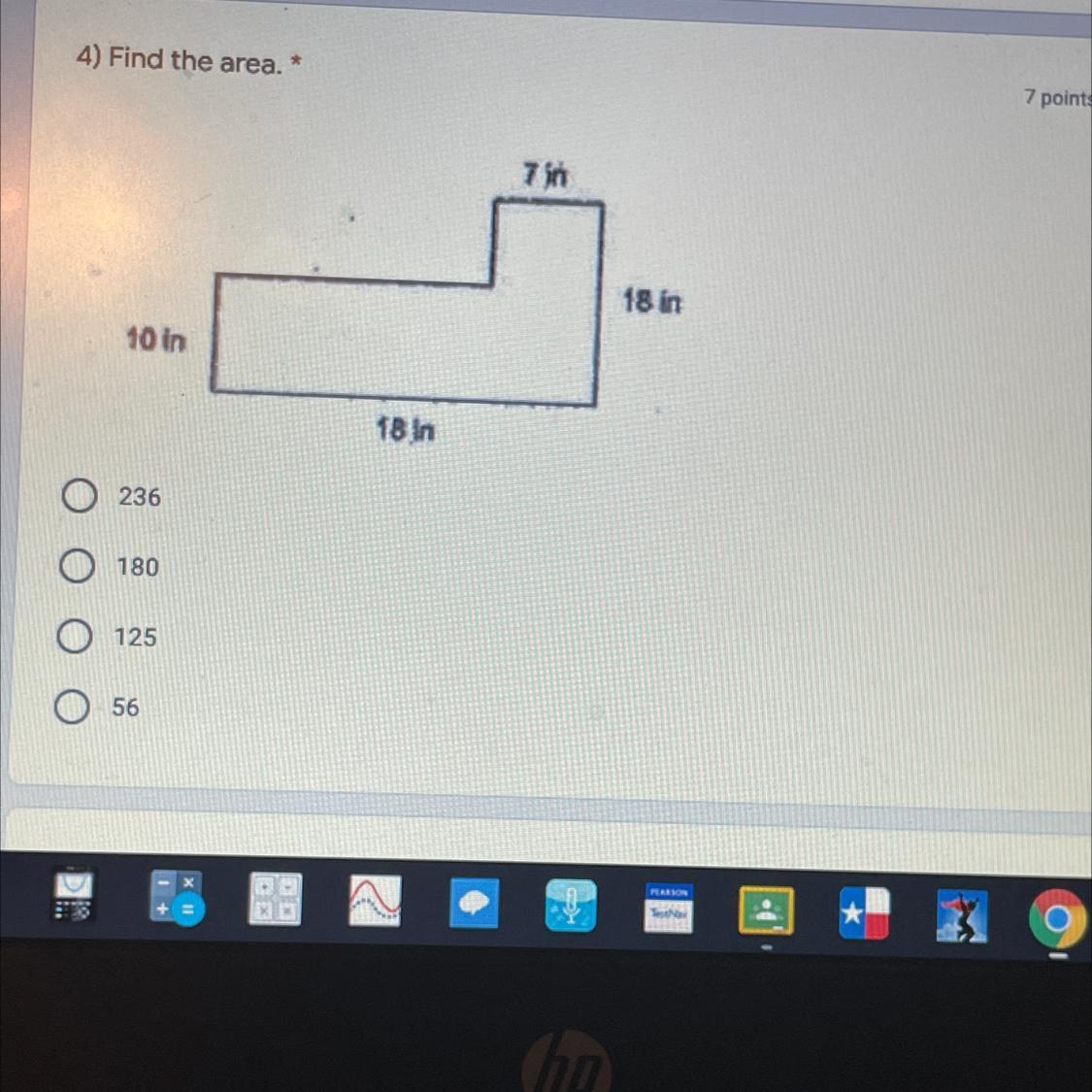
4) Find the area.
7 points
7 in
18 in
10 in
18 in
236
180
125
56
Answers
Answer: its 236
Step-by-step explan
A heat teacher shared 60 notebook amoung 6 students one of the student found that each of his book contained 200 page. How many pages were in all the books he received?
Answers
Answer:
2,000 pages.
Step-by-step explanation:
The heat teacher has 60 notebooks in total. If the teacher evenly distributed the notebooks among the 6 students, then that would be
60 ÷ 6 = 10 notebooks to each student.
Now let's say a kid named Ethan found out each of his notebooks contains 200 pages. Ethan has 10 notebooks in total so he needs to do
10 × 200 = 2,000 pages in total.
We do 10 × 200 since Ethan has 10 notebooks, and each of his notebooks have 200 pages.
Thus 2,000 is the answer.
very easy trig with pic

Answers
Answer:
1st Option
Step-by-step explanation:
Pythagorean Theorem: a² + b² = c²
Step 1: Find the missing leg
2² + b² = 6²
b² = 36 - 4
b = √32
Step 2: Find cosA
cosA = √32/6
cosA = 4√2/6
cosA = 2√2/3
helloo!! i need help figuring out the like terms in this list. thanks! :)

Answers
The like terms on the list are given as follows:
\(\sqrt{2}, -3\sqrt{2}, 5\sqrt{2}, \sqrt{50}\)
What are like terms?Like terms are terms that share these two features:
Same letters. (algebraic variables).Same exponents.If two terms are like terms, then they can be either added or subtracted.
In the case the terms are roots, they have the same root.
The square root of 50 is given as follows:
\(\sqrt{50} = \sqrt{2 \times 25} = 5\sqrt{2}\)
Hence the like terms are given as follows:
\(\sqrt{2}, -3\sqrt{2}, 5\sqrt{2}, \sqrt{50}\)
There are no terms with 3 or 5 on the root, hence the other two terms have no like terms.
More can be learned about like terms at brainly.com/question/17471184
#SPJ1
Point s is on line segment rt. given rt = 19 and rs = 6, determine the length st
Answers
Under the consideration of collinearity of two line segments, the length of the line segment ST is equal to 13.
What is the length of a line segment collinear to another line segment?
According to the statement seen in this question, the line segments RT and ST are collinear to each other. Mathematically speaking, the length of the line segment ST can be found by using the following formula:
RT = RS + ST
ST = RT - RS
ST = 19 - 6
ST = 13
Under the consideration of collinearity of two line segments, the length of the line segment ST is equal to 13.
To learn more on line segments: https://brainly.com/question/25727583
#SPJ1
Draw a A PQR if PQ = 6.5cm, m< PQR=75 °and m <PRQ=45° using ruler and compasses
only.
Answers
Answer:
Check your question well
Step-by-step explanation:
U didn't ask to draw angle p so how can we get the angle r

How do you draw a bar model for "5y=95" "6b=12" "168/c=8" " v / 7=5"
will give full brainliest if someone shows me a demenstation pls help asap
Answers
The solution is given below.
What is Bar model?In maths a bar model is a pictorial representation of a problem or concept where bars or boxes are used to represent the known and unknown quantities. Bar models are most often used to solve number problems with the four operations – addition and subtraction, multiplication and division.
here, we have,
"5y=95"
"6b=12"
"168/c=8"
" v / 7=5"
so, the bar model ,
y = 95/5
=19
b= 12/6
= 2
c = 168/8
= 21
v = 5* 7
= 35
To learn m ore on bar model click;
https://brainly.com/question/21237674
#SPJ1
PART 3 PLZ ANSWER 32 POINTS

Answers
i think you can do this one : )
If your good at Geometric Congruence, please answer the questions below in the photos. Please help, thank you.





Answers
Answer:
X=22 because of the symmetrical angle so 158+158=316 and one full angle = 360 then 360-316=44 and there are two sides so 44÷2=22
Find the area of polygon
Plsss help is for my tmrw finals

Answers
The area of each polygon in this problem is given as follows:
a) 252 square units.
b) 65 square units.
How to obtain the area of each polygon?For item a, we have a rectangle of dimensions 12 and 21, hence the area is the multiplication of the dimensions, as follows:
A = 12 x 21 = 252 square units.
For item b, we have a triangle with base 13 and height 10, hence the area is half the multiplication of the base by the height, as follows:
A = 0.5 x 13 x 10 = 65 square units.
More can be learned about the area of a polygon at https://brainly.com/question/8409681
#SPJ1
the lengths of the sides of a triangle are 16, 31, and x, where x is the shortest side. if the triangle is not isosceles, what is a possible value of x?
Answers
Answer:
16 + x > 31, so x > 15
16 + 31 > x, so x < 47
Combining these inequalities, we have
15 < x < 47.
Since x is the shortest side of this triangle, and since the triangle is not isosceles,
15 < x < 16. So one possible value of x is 15.1.
Is 1 hour is 9 miles, how many hours is 15 miles?
1 hr = 9 mi
__hr = 15 mi
Answers
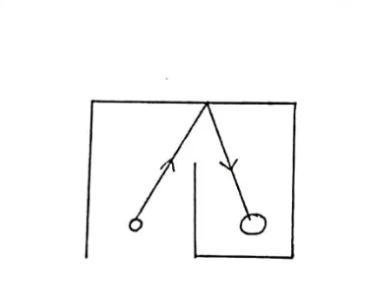
Jacob is playing miniature golf. He states that he cannot hit the ball from the start, bounce it off the back wall once, and reach the hole in one shot. Is Jacob correct? Label the diagram to support your answer.

Answers
Jacob is playing miniature golf, then the ball is can not reach the hole in one shot, so Jacob is correct.
Jacob is playing miniature golf.
He states that he cannot hit the ball from the start.
Bounce it off the back wall once
And reach the hole in one shot.
So, we can write,
The ball is need to bounce off the back wall once.
The ball is can not reach the hole in one shot.
Jacob is correct.
It is not possible to hit the ball from the start,
Bounce it off the back wall once,
And reach the hole in one shot.
Therefore, Jacob is playing miniature golf, Then the Jacob is correct.
To learn more about visit miniature golf :
brainly.com/question/15682780
#SPJ1
Represent constraints by equations or inequalities, and by systems of equations and/or inequalities, and interpret solutions as viable or non-viable options in a modeling context.
Answers
constraints in mathematical modeling can be represented using equations or inequalities, as well as systems of equations and/or inequalities.
In mathematical modeling, constraints are conditions or limitations that restrict the possible values or solutions of a problem. They can be represented using equations or inequalities, as well as systems of equations and/or inequalities. The solutions to these constraints can then be interpreted as viable or non-viable options within the context of the model.
Here are a few examples to illustrate the representation of constraints and the interpretation of solutions:
Example 1: Production Constraints
Let's say we are modeling a production process where we have limited resources. We have a constraint that the total number of units produced cannot exceed 100. We can represent this constraint as an inequality:
x ≤ 100
where x represents the total number of units produced. The solution to this constraint would be any value of x that is less than or equal to 100. Any value greater than 100 would be a non-viable option within the context of the production process.
Example 2: Budget Constraints
Suppose we are creating a budget for a project and have a constraint that the total expenses cannot exceed $5000. We can represent this constraint as an equation:
x + y + z = 5000
where x, y, and z represent different expense categories. The solution to this constraint would be any combination of values for x, y, and z that sum up to 5000. Any combination that exceeds 5000 would be non-viable within the budget constraints.
Example 3: Optimization Problem
Consider an optimization problem where we want to maximize a certain objective function subject to certain constraints. For instance, suppose we want to maximize the area of a rectangular garden while having a fixed perimeter of 40 meters. We can represent this problem using equations and inequalities:
2x + 2y = 40 (perimeter constraint)
Area = x * y (objective function)
The solution to this problem would be the values of x and y that satisfy the perimeter constraint while maximizing the area. These solutions would be the viable options within the context of the garden design.
In summary, constraints in mathematical modeling can be represented using equations or inequalities, as well as systems of equations and/or inequalities. The solutions to these constraints represent the viable or non-viable options within the context of the model, and they help guide decision-making and problem-solving processes.
Learn more about mathematical modeling here
https://brainly.com/question/731147
#SPJ4
for all m, n ∈ a, m r n ⇔ 5|(m2 − n2). it is a fact that r is an equivalence relation on a. use set-roster notation to list the distinct equivalence classes of r. (enter your answer as a comma-separated list of sets.)
Answers
To find the distinct equivalence classes of the relation "r," we need to determine the sets of elements in set "a" that are related to each other based on the given condition. In this case, the condition is that for any "m" and "n" in set "a," "m r n" if and only if "5|(m^2 - n^2)."
To list the distinct equivalence classes using set-roster notation, we need to identify sets of elements that are related to each other under the relation "r." Let's proceed with finding these sets:
Start by picking an arbitrary element "x" from set "a."
Identify all elements "y" in set "a" such that "x r y." In other words, find elements that satisfy the condition "5|(x^2 - y^2)."
Repeat steps 1 and 2 until all elements in set "a" have been considered.
Group all elements found in step 2 for each iteration into distinct sets.
For instance, let's assume set "a" contains the elements {1, 2, 3, 4, 5}. We will go through the steps mentioned above:
Pick 1 from set "a."
Identify elements related to 1: 1 r 4 (since 5|(1^2 - 4^2)), and 1 r 3 (since 5|(1^2 - 3^2)).
Repeat steps 1 and 2 for the remaining elements: 2 r 5 (since 5|(2^2 - 5^2)).
Group the elements found in step 2 into sets: {1, 4, 3}, and {2, 5}.
Therefore, the distinct equivalence classes of "r" are {1, 4, 3} and {2, 5}. The distinct equivalence classes of the relation "r" on set "a" are {1, 4, 3} and {2, 5}. To find the distinct equivalence classes, we need to determine sets of elements in set "a" that are related to each other under the relation "r." The relation "r" is defined as "5|(m^2 - n^2)." This means that for any elements "m" and "n" in set "a," "m r n" if and only if "5" divides the difference between the squares of "m" and "n." Using the set-roster notation, we can list the distinct equivalence classes as {1, 4, 3} and {2, 5}. These sets represent elements that are related to each other based on the given condition. To find these sets, we follow the steps outlined above. Starting with an arbitrary element from set "a," we identify all elements related to it. We repeat this process for all elements in set "a" and group the related elements into distinct sets.
The distinct equivalence classes of the relation "r" on set "a" are {1, 4, 3} and {2, 5}. These sets represent elements that are related to each other based on the given condition "5|(m^2 - n^2)."
To learn more about set-roster notation visit:
brainly.com/question/31981752
#SPJ11
ΔXYZ was reflected to form ΔLMN.
Triangle X Y Z is reflected to from triangle L M N. Angle Z Y X is 86 degrees and angle Y X Z is 38 degrees. Angle L N M is 56 degrees and angle N M L is 86 degrees.
Which statements are true regarding the diagram? Check all that apply.
Answers
Answer:
A,B,C, and F
Step-by-step explanation:
Edge 2020
Answer:
A. B. C. and F.
Step-by-step explanation:
PLEASE find x!!!!!!thx

Answers
Answer:
A.
Step-by-step explanation:
Find the scale by dividing 80 by 48 you get 1.6 then multiply by 60
Answer: A
Step-by-step explanation:
hey I suck at algebra so some help would be nice HAHA

Answers
fill in the missing number: 0,1,1,2,3,5,8,13,-,34,55
Answers
The missing number of the series is 21.
The given sequence appears to follow the pattern of the Fibonacci sequence, where each number is the sum of the two preceding numbers. The Fibonacci sequence starts with 0 and 1, and each subsequent number is obtained by adding the two previous numbers.
Using this pattern, we can determine the missing number in the sequence.
0, 1, 1, 2, 3, 5, 8, 13, -, 34, 55
Looking at the pattern, we can see that the missing number is obtained by adding 8 and 13, which gives us 21.
Therefore, the completed sequence is:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55.
To learn more about number here:
https://brainly.com/question/32210789
#SPJ4
The missing number in the sequence 0, 1, 1, 2, 3, 5, 8, 13, -, 34, 55 is 21.
To find the missing number in the sequence 0, 1, 1, 2, 3, 5, 8, 13, -, 34, 55, we can observe that each number is the sum of the two preceding numbers. This pattern is known as the Fibonacci sequence.
The Fibonacci sequence starts with 0 and 1. To generate the next number, we add the two preceding numbers: 0 + 1 = 1. Continuing this pattern, we get:
011235813213455Therefore, the missing number in the sequence is 21.
Learn more:About fill in here:
https://brainly.com/question/182137
#SPJ11
1. What is the mean change in the forecasted high temperatures over the next 7 days? Remember, this can be found by averaging the values in the Difference column for the high temperatures. Show your work and steps. If your answer is not an integer, explain what two integers your answer is between. 2. What is the mean change in the forecasted low temperatures over the next 7 days? Remember, this can be found by averaging the values in the Difference column for the low temperatures. If your answer is not an integer, explain what two integers your answer is between.
Answers
Answer:
The table is missing in the question. The table is provided below.
Step-by-step explanation:
1. In the table, it is given the difference of high temperature. They are :
-7, -7, 2, 5, -3, -2
Now adding the differences of high temperatures and taking out its average.
-7 + (-7) + 2 + 5 + (-3) + (-2)= -12
Average : \($-\frac{12}{6}=-2$\)
Thus the answer is an integer.
2. In the table, it is given the difference of high temperature. They are :
0, -3, -7, -1, 1, 0
Now adding the differences of high temperatures and taking out its average.
0 + (-3) + (-7 )+ (-1) + 1 + 0= -10
Average : \($-\frac{10}{6} = -1.66$\)
Thus, the answer is not an integer. The answer lies between the integers -2 to -1.

Answer:
Ok to clear some question the top guy got 6 because there are 6 numbers
Step-by-step explanation:
Input : 3 4 5 4 6 output: 20 25 30 35 40 (function or non function)
Answers
Answer:
no it isn't
because there are two 4 with differents outputs
Step-by-step explanation:
Answer:
No, it is not a function.
Step-by-step explanation:
There are two outputs for the same input of 4.
Solve the pair of simultaneous equations and leave the answer as a fraction in
its lowest term. 2x − 3 = y, x+ y= 8
Answers
Answer:
x = 11/3 = 3 2/3
y = 13/3 = 4 1/3
Step-by-step explanation:
Here, we want to solve the system of equations simultaneously
x + y = 8
2x -3 = y
From the second equation, we have an equation for y
we can simply proceed to substitute this into the first equation
x + 2x - 3 = 8
3x - 3 = 8
3x = 8 + 3
3x = 11
x = 11/3
Recall;
y = 2x - 3
y = 2(11/3) - 3
y = 22/3 - 3
y = (22-3(3))/3
y = (22-9)/3 = 13/3
Alan ran twice as many miles on Tuesday as he did on Monday and five more miles on Wednesday than he did on Monday. Write and evaluate an expression to find the total number of miles he ran if he ran 5 miles on Monday
Answers
Answer:
The answer is 25
Step-by-step explanation:
If he ran 5 on Monday, twice that is 10, and 10+5 is 15. Also, 5+5 is 10, and 15+10 is 25.
Consider the polynomial 9n2+60n+100.
What are the square roots of the first and last terms?
square root of first term:
square root of last term:
Answers
Last term: 10
Have a great day :)
Please help if it is answered in 5 minutes i will give brainliest

Answers
Can I get a answer for all of it?

Answers
Answer:
R'=(-3,6)
Q'=(-3,-3)
S'=(7,6)
T'=(7,-3)
Answer:
see explanation
Step-by-step explanation:
A translation of 7 units right means adding 7 to the x- coordinate. The y- coordinate remains unchanged, then
Q (- 10, - 3 ) → Q' (- 10 + 7, - 3 ) → Q' (- 3, - 3 )
R (- 10, 6 ) → R' (- 10 + 7, 6 ) → R' (- 3, 6 )
S (0, 6 ) → S' (0 + 7, 6 ) → S' (7, 6 )
T (0, - 3 ) → T' (0 + 7, - 3 ) → T' (7, - 3 )
Given r(x) =x' - 4x2 + 4x - 6, find the value of r(2). What does your answer tell you about x - 2 as a factor of r(x)? Explain.
Answers
We can conclude that the value of r(2) which is -6 and x - 2 is not the factor for r(x).
What is Factor?A function that accepts a real number as input, typically represented by the variable x and outputs another real number, typically the value of the function denoted by f is known as a real-valued function of a real variable (x).Any polynomial that is divisible by the polynomial P(x) is a factor of that polynomial (x).So, we know that the equation is:
r(x)=x^3-4x^2+4x-6:Now, calculate the equation when x = 2.
r(2)=2^3-4(2)^2+4(2)-6r(2)=8-16+8-6r(2)=-6Now, we can conclude that:
As we see that x=2 is not equal to zero.Implies x-2 does not divide r(x) evenly.Thus x-2 is not a factor of given r(x).Therefore, we can conclude that the value of r(2) which is -6 and x - 2 is not the factor for r(x).
Learn more about factors here:
brainly.com/question/24380382
#SPJ13
6 = −w/8 solve
what is w?
Answers
Answer:
w = -48
Step-by-step explanation:
6 = -w/8
6*8 = (-w/8) * 8 => 48 = -w
(-1) * 48 = (-1) * (-w) => -48 = w => w = -48
Multiply both sides of the equation by 8.
48 = −wSwap the sides so that all the terms of the variables are on the left side.
−w = 48Multiply both sides by −1.
w = −48Given: abcd is a rectangle, M is midpoint of line AB prove: line DM is congruent to CM
Answers
DM is congruent to line CM because CDM is congruent to triangle CBM using the SAS congruence criteria for triangles.
Draw a diagram of the rectangle ABCD with M as the midpoint of AB. Draw lines CM and DM ( refer to the attached image). Since AB is a line segment, we know that AM is congruent to MB (because M is the midpoint of AB). Since ABCD is a rectangle, we know that AB is parallel to CD, and AD is parallel to BC. Thus, we have two pairs of parallel lines: AB and CD, and AD and BC.
Using the fact that opposite sides of a rectangle are congruent, we have CD = AB. Now, we have a pair of congruent sides (DM and CM) that are opposite each other in triangle CDM and CBM respectively. We also have another pair of congruent sides (CD and AB) that are opposite each other in both triangles. Finally, we know that the angle CMD is congruent to the angle CMB because they are vertical angles. By the Side-Angle-Side (SAS) congruence criterion, we can conclude that triangle CDM is congruent to triangle CBM.
Therefore, line DM is congruent to line CM by SAS congruence criteria.
To learn more about congruence, refer to:
https://brainly.com/question/30094441
#SPJ4

ii) What is the base of and exponent of −24 ? Base: Exponent:
Answers
The base and exponent of −2^4 are
Base: -2
Exponent: 4
How to determine the base and the exponentFrom the question, we have the following parameters that can be used in our computation:
-2^4
In the expression -2^4, -2 is the base and 4 is the exponent.
The base is the number that is being multiplied by itself and the exponent is the number of times the base is being multiplied by itself.
In this case the base is -2 and the exponent is 4.
So the expression -2^4 means -2 multiplied by itself 4 times.
Read more about expression at
https://brainly.com/question/15775046
#SPJ1