The distance between two locations on a map is 6 centimeters (cm). If 1 cm on the map corresponds to an actual distance of 15 miles,
what is the actual distance, in miles, between the two locations?
04
Answers
Answer:
Step-by-step explanation:
6x15=90
90miles
Related Questions
Two years ago, the water level in a local reservoir fell 834 feet. Last year, the water level rose 435 feet. By how many feet did the water level of the reservoir change overall during these two years?
Answers
Answer:
- 4 3/20 The other person is correct
Step-by-step explanation:
The water is 399 feet fell.
What is unitary Method?The unitary technique involves first determining the value of a single unit, followed by the value of the necessary number of units.
For example, Let's say Ram spends 36 Rs. for a dozen (12) bananas.
12 bananas will set you back 36 Rs. 1 banana costs 36 x 12 = 3 Rupees.
As a result, one banana costs three rupees. Let's say we need to calculate the price of 15 bananas.
This may be done as follows: 15 bananas cost 3 rupees each; 15 units cost 45 rupees.
Given:
Two years ago, the water level in a local reservoir fell 834 feet.
Last year, the water level rose 435 feet.
So, the water level of the reservoir change overall during these two years
= -834 + 435
= -399
Hence, the water is 399 feet fell.
Learn more about Unitary Method here:
https://brainly.com/question/22056199
#SPJ2
May someone help me out with this. A bit lost here. If anyone knows, and would like to answer, I would gladly appreciate you. Thanks.

Answers
Answer:
since they are parallel lines therefore the angles hence formed will also be equal
x+5=2x-7
5+7=2x-x
12=x
hence the ans is 12
plz mark it as brainliest
your bill was $93.50 and the tax was 6.25%
how much was the tax
How much was the total bill?
Answers
Answer:
$99.34
Step-by-step explanation:
sociologists say that 80% of married women claim that their husband's mother is the biggest bone of contention in their marriages (sex and money are lower-rated areas of contention). suppose that eleven married women are having coffee together one morning. find the following probabilities. (round your answers to three decimal places.) a button hyperlink to the salt program that reads: use salt. (a) all of them dislike their mother-in-law. (b) none of them dislike their mother-in-law. (c) at least nine of them dislike their mother-in-law. (d) no more than eight of them dislike their mother-in-law.
Answers
(a) The probability that all 11 women dislike their mother-in-law is approximately 0.209.
(b) The probability that none of the 11 women dislike their mother-in-law is approximately 0.002.
(c) The probability that at least nine of the 11 women dislike their mother-in-law is approximately 0.995.
(d) The probability that no more than eight of the 11 women dislike their mother-in-law is approximately 0.996.
This problem can be approached using the binomial distribution, which models the number of successes in a fixed number of independent trials with the same probability of success.
Let p be the probability that a randomly chosen married woman dislikes her mother-in-law, based on the sociologists' claim. Then, we have p = 0.8.
(a) To find the probability that all 11 women dislike their mother-in-law, we can use the binomial distribution with n = 11 and p = 0.8:
P(X = 11) = (11 choose 11) × 0.8^11 × 0.2^0 ≈ 0.209
(b) To find the probability that none of the 11 women dislike their mother-in-law, we can use the binomial distribution again
P(X = 0) = (11 choose 0) × 0.8^0 × 0.2^11 ≈ 0.002
(c) To find the probability that at least nine of the 11 women dislike their mother-in-law, we can use the complement rule and find the probability that fewer than nine dislike their mother-in-law
P(X < 9) = P(X = 0) + P(X = 1) + ... + P(X = 8)
Using the binomial distribution for each term, we get
P(X < 9) ≈ 0.005
Therefore, the probability that at least nine of the 11 women dislike their mother-in-law is approximately 1 - 0.005 = 0.995.
(d) To find the probability that no more than eight of the 11 women dislike their mother-in-law, we can again use the binomial distribution and add up the probabilities of X = 0, 1, ..., 8:
P(X ≤ 8) = P(X = 0) + P(X = 1) + ... + P(X = 8)
Using the binomial distribution for each term, we get
P(X ≤ 8) ≈ 0.996
Learn more about probability here
brainly.com/question/29350029
#SPJ4
Using the given symbolization key, translate each English-language assertion into Propositional Logic. E1: Ava is an electrician. E2: Harrison is an electrician. F1: Ava is a firefighter. F2: Harrison is a firefighter. S1: Ava is satisfied with her career. S2: Harrison is satisfied with his career. 1) If Ava is not an electrician, then neither is Harrison, but if she is, then he is too. 2) Ava is satisfied with her career if and only if Harrison is not satisfied with his. 3) Harrison and Ava are both firefighters if and only if neither of them is an electrician.
Answers
If Ava is not an electrician, then Harrison is not an electrician, but if Ava is an electrician, then Harrison is an electrician.
Symbolization in Propositional Logic:
Let S represent "Ava is satisfied with her career"
Let T represent "Harrison is satisfied with his career"
b) Ava is satisfied with her career if and only if Harrison is not satisfied with his.
Translation: S ↔ ~T
The statement uses the biconditional operator "if and only if" to establish an equivalence between Ava's satisfaction with her career and Harrison's lack of satisfaction with his career. It is symbolized as S ↔ ~T, where S represents Ava's satisfaction and ~T represents Harrison's lack of satisfaction.
The biconditional operator ensures that both sides of the statement are equivalent. If Ava is satisfied with her career, then Harrison must not be satisfied with his career, and vice versa. The statement establishes a direct relationship between the satisfaction levels of Ava and Harrison.
Learn more about Equivalent expression click here :brainly.com/question/14083225
#SPJ11
One of the criticisms of the Social Readjustment Rating Scale is that it does NOT take into account:
Answers
What is one major limitation of the Social Readjustment Rating Scale?
The Social Readjustment Rating Scale has severe limitations, despite being a helpful tool for the research of life transition and disease. The current measure cannot be used to assess the impact of various life changes (such as positive or negative ones) on the development of sickness.Learn more about Social Readjustment Rating Scale brainly.com/question/13044228
#SPJ4
A bouncy ball is dropped such that the height of its first bounce is 4.5 feet and each successive bounce is 73% of the previous bounce's height. What would be the height of the 10th bounce of the ball? Round to the nearest tenth (if necessary).
Answers
The height of the 10th bounce of the ball will be 0.6 feet.
What is geometric sequence?A geometric sequence is a sequence in which each term is found by multiplying the preceding term by the same value.
What is the formula for finding the nth term of geometric sequence?The nth term of the geometric sequence is given by
\(\sf T_n=ar^{n-1}\)
Where,
\(\sf T_n\) is the nth term.r is the common ratioa is the first termAccording to the given question.
During the first bounce, height of the ball from the ground, a = 4.5 feet
And, the each successive bounce is 73% of the previous bounce's height.
So,
During the second bounce, the height of ball from the ground
\(\sf = 73\% \ of \ 10\)
\(=\dfrac{73}{100}(10)\)
\(\sf = 0.73 \times 10\)
\(\sf = 7.3 \ feet\)
During the third bounce, the height of ball from the ground
\(\sf = 73\% \ of \ 7.3\)
\(=\dfrac{73}{100}(7.3)\)
\(\sf = 5.33 \ feet\)
Like this we will obtain a geometric sequence 7.3, 5.33, 3.11, 2.23,...
And the common ratio of the geometric sequence is 0.73
Therefore,
The sixth term of the geometric sequence is given by
\(\sf T_{10}=10(0.73)^{10-1\)
\(\sf T_{10}=10(0.73)^{9\)
\(\sf T_{10}=10(0.059)\)
\(\sf T_{10}=0.59\thickapprox0.6 \ feet\)
Hence, the height of the 10th bounce of the ball will be 0.6 feet.
Find out more information about geometric sequence here:
brainly.com/question/11266123
.Two angles form a linear pair. The measure of one
angle is 1/3 the measure of the other angle.
Answers
Answer:
45o and 135o
Step-by-step explanation:
The sum of angles of a linear pair is always equal to 180°.
So if the first angle is x,
then the second angle is 3x
x + 3x = 180
4x = 180
x = 45
then 3x = 135
A 7-digit telephone number has the form abc - xxxx, where x, b, and c can be any digit 1 - 9 and a is restricted to 3 - 9. how many numbers are possible?
Answers
The number of possible numbers in the given format is 7 × 9 × 9 × 9 × 10⁴, there are 567,000,000 possible telephone numbers in the given format.
In the given telephone number format, there are 7 digits, denoted by abc - xxxx.
The digit a is restricted to the range 3 - 9, so there are 7 possible choices for a.
The digits b and c can be any digit from 1 - 9, so there are 9 possible choices for each of them.
For the remaining digits x, they can be any digit from 0 - 9, resulting in 10 choices for each x. Since there are 4 x's in the format, we have 10⁴ choices for these digits.
To calculate the total number of possible telephone numbers, we multiply the number of choices for each digit: 7 × 9 × 9 × 9 × 10⁴ = 7 × 9³ × 10⁴ = 7 × 9⁴ × 10⁴ = 7 × 9⁴ × (10²)² = 7 × (9²)² × (10²)² = 7 × 81 × 10⁴ × 10⁴ = 7 × 81 × (10⁴)² = 7 × 81 × 10⁸ = 567 × 10⁸ = 567,000,000.
learn more about Possible numbers
https://brainly.com/question/29208955
#SPJ11
WILL GIVE BRAINLIEST!
The Ride for Health Bicycle Club has chosen a 36-mile course for this Saturday's ride. If the riders plan on averaging 12 mph while they are riding, and they have a 1-hour lunch break planned, how long will it take them to complete the trip?
hr
Answers
Answer:
4 hours
Step-by-step explanation:
It is 4 hours because you do 36 divide by 12 which is 4, Then you do 4x1= 4
write 9.6 x 10^9 as a normal number
Answers
Answer:
Step-by-step explanation:
9.6×10^9=96/10 ×10^9=96×10^8=9,600,000,000
In a game of chess, a player can either
win, draw or lose.
The probability that Vishi wins any
game of chess is 0.5
The probability that Vishi draws any
game of chess is 0.3
Vishi plays two games of chess.
Work out the probability that Vishi will
lose exactly one of the two games.
Pls answer fast
Answers
Answer:
0.14
Step-by-step explanation:
If winning holds a probability of 0.5 and a draw holds a probability of 0.3, then that means that losing has a probability of 0.2 (1 - 0.5 - 0.7 = 0.2). Therefore, to find the probability of Vishi losing exactly one of the two games we need to multiply the probability of him losing one game by the probability of him winning or tying the second game like so...
0.2 * (0.5 + 0.3) = x
0.2 * 0.7 = x
0.14 = x
Finally, we can see that the probability of Vishi losing exactly one of the two games is 0.14
Your company wants to purchase some equipment for recycling metals. Machine A costs $323,000 and has a useful life of 10 years. Its operating costs are $2.40 per ton of metal processed. Machine B costs $178,000 and has a useful life of 6 years. Its operating costs are $8.00 per ton of metal processed. How many tons of metal per year must your company process to favor Machine A over Machine B? Assume an MARR of 18% per year.
Previous question
Next question
Answers
To determine the number of tons of metal per year needed for Machine A to be favored over Machine B, we compare their costs. Machine A costs $323,000 with an annual operating cost of $2.40/ton, while Machine B costs $178,000 with an annual operating cost of $8.00/ton. The machines have useful lives of 10 years and 6 years, respectively, and the minimum attractive rate of return (MARR) is 18% per year.
By calculating the equivalent annual costs (EAC) for each machine using the given formula and comparing them, we can determine the point at which Machine A becomes more favorable. However, specific values for the discounting factors and the tons per year needed are missing, making it impossible to provide an exact answer.
Learn more about investment analysis here: brainly.com/question/32546870
#SPJ11
what does x= x+5*4+3=9
Answers
Answer:
x = -14.
Step-by-step explanation:
x + 5 * 4 + 3 = 9
x + 20 + 3 = 9
x + 23 = 9
x = -14
Hope this helps!
The inequality graphed below represents the ages, a, of
players on a baseball team.
Which inequality represents the same ages?
0 12 < a < 18
10 11 12 13 14 15 16 17 18 19 20
o 12 sa< 18
0 12 >as 18
O 122 a< 18
Answers
Answer:
the first one
Step-by-step explanation:
the others don't make any sense and also the first one's the only one that's in inequality form.
The inequality that represents the ages is 12 ≤ a ≤ 18.
What is inequality?It shows a relationship between two numbers or two expressions.
There are commonly used four inequalities:
Less than = <
Greater than = >
Less than and equal = ≤
Greater than and equal = ≥
We have,
The inequality graphed below is shown.
The number line includes the numbers 12 and 18.
So,
The ages of the baseball team are 12 to 18.
This can be written as,
12 ≤ a ≤ 18
Thus,
The inequality that represents the ages is 12 ≤ a ≤ 18.
Learn more about inequalities here:
https://brainly.com/question/20383699
#SPJ7

10y 5 +30y 3 −15y
Factor out the gcf then simplify the polynomial
Answers
10y⁵ + 30y³ - 15y =
5y * 2y⁴ + 5y * 6y² + 5y * (-3) =
5y (2y⁴ + 6y² - 3)
Determine P(c) using the remainder theorem.. (look at image)
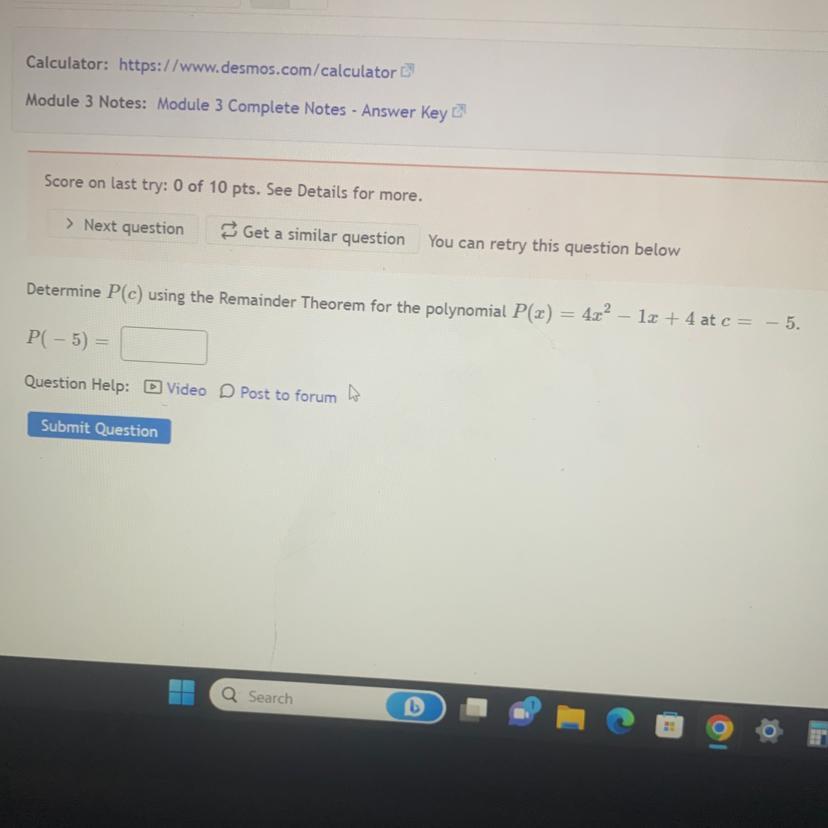
Answers
Answer:
P(-5) = 109
Step-by-step explanation:
Remainder theorem:If the polynomial p(x) is divided by the linear polynomial (x-a), the remainder is p(a).
Dividend = divisor * quotient + remainder.
p(x) = (x-a) * q(x) + p(a)
Here, q(x) is the quotient and p(a) is the remainder.
P(x) = 4x² - x + 4
P(-5) = 4*(-5)² - 1*(-5) + 4
= 4*25 + 5 + 4
= 100 + 5 + 4
= 109
Find the 4th term in the sequencewith the following definition:aj = 0an = 2(an-1-3)

Answers
Answer:
-60
Explanation:
To find the 4th term we need to also find the 2nd and 3rd terms as follows:
\(\begin{gathered} a_n=2(a_{n-1}-3) \\ a_2=2(a_{2-1}-3) \\ a_2=2(a_1-3) \\ a_2=2(0-3) \\ a_2=2(-3) \\ a_2=-6 \end{gathered}\)\(\begin{gathered} a_3=2(a_{_2}-3) \\ a_3=2(-6-3) \\ a_3=3(-9) \\ a_3=-27 \end{gathered}\)Finally, we can calculate the value of the 4th term as:
\(\begin{gathered} a_4=2(a_3-3) \\ a_4=2(-27-3) \\ a_4=2(-30) \\ a_4=-60 \end{gathered}\)So, the answer is -60
Assume that an image is created by rotating another figure 180 degrees. Explain how you can you could determine the location of the center of rotation
Answers
Answer:
60 degree and 120 degree
(Using trig to find a side)
Solve for x. Round to the nearest tenth, if necessary.

Answers
Value of hypotenuse x in the triangle is 9.4.
Define trigonometric functionA trigonometric function is a mathematical function that relates the angles of a triangle to the ratios of the sides of the triangle. The sine, cosine, and tangent functions—abbreviated as sin, cos, and tan, respectively—are the three most used trigonometric operations. Other trigonometric functions include the cosecant (csc), secant (sec), and cotangent (cot) functions. These functions are used extensively in mathematics, science, and engineering to model periodic phenomena, such as sound and light waves, and to solve problems related to geometry and trigonometry.
Given triangle is right angled triangle.
base of triangle=8
hypotenuse of triangle=x
Using trigonometric function,
Cosθ=base/Hypotenuse
For θ=30°,
Cos32°=b/h
cos32°=8/x
x=8/cos32°
x=8/0.84
x=9.4
To know more about triangle, visit:
https://brainly.com/question/2773823
#SPJ1
13 < -2x + 5
ps: the “<“ has a _ under it i can’t type that but yeah , I really need help
Answers
Answer:
x<-4
Step-by-step explanation:
To solve this problem, follow these steps:
1. Subtract 5 from both sides.
13<-2x+5
13(-5)<-2x+5(-5)
2. Simplify.
(8)<-2x+5-5
3. Subtract the 5's. And bring down the new equation.
8<-2x+5-5
8<-2x
4. Divide -2x on both sides.
8/-2<-2x/-2
5. Simplify and cancel out the -2's.
-4<x
6. Move the variable to the left and flip the inequality.
x<-4
Evaluate 68 % of 948.37 m Give your answer rounded to 2 DP.
Answers
Answer:
644.89
Step-by-step explanation:
Answer:
644.89 m
Step-by-step explanation:
68 / 100 * 948.37 = 0.68 * 948.37 = 644.89 m (2 d.p.)
6,6 and 7 units down and 5 units left where is t'
Answers
Answer:
it's 1,-1
Step-by-step explanation:
hoped I helped. I'm good at these.
For which system of inequalities is (-3, 1) a solution?
x+y<-2 and 2x-3y <-9
x+y<-2 and 2x-3y <-9
x+y≤-2 and 2x-3y <-9
x+y≤-2 and 2x-3y ≤-9
Answers
In light of the query we've got D)x + y ≤ -2 and 2x - 3y ≤ -9 is a pair of inequalities for (-3, 1) is the correct answer.
How may an inequality be resolved?When resolving an inequality, you can do one of the following: · Add a same number to each side; • Subtract the same amount from each side; • Multiply or divide either aspect by the exact positive amount. You must flip the inequality sign if you combine or split each end by a negative number.
According to the values x = -3, y = 1
-3 + 1 = -2, which is less than or equal to -2, so the first inequality is true.
2 * -3 - 3 * 1 = -9, which is less than or equal to -9, so the second inequality is also true.
Since both inequalities are true, (-3, 1) is a solution for the system of inequalities x + y ≤ -2 and 2x - 3y ≤ -9.
we get ,
x + y ≤ -2
2x - 3y ≤ -9
To know more about Inequalities visit :
https://brainly.com/question/19003099
#SPJ1
The Complete Question :
For which system of inequalities is (-3, 1) a solution?
A. x+y<-2 and 2x-3y <-9
B. x+y<-2 and 2x-3y <-9
C. x+y≤-2 and 2x-3y <-9
D. x+y≤-2 and 2x-3y ≤-9
John earned $400 interest at a rate of 6% for 3 years how much money did John originally invest
Answers
John earned $400 interest at a rate of 6% for 3 years. Therefore, the amount of money John originally invested was $2,222.22.
We are able to use the Simple interest formula to resolve this problem:
Simple interest is a simple concept in finance that is used to calculate the interest earned or paid on a essential amount over a positive time period.
Simple interest = (principal x charge x time)
Given that John earned $400 in interest at a price of 6% for three years, we are able to set up the equation as:
400 = (P x 0.06 x 3)
In which P is the principal (the original amount invested).
Simplifying this equation, we get:
400 = 0.18P
Dividing both facets through 0.18, we get:
P = $2,222.22
Thus, John originally invested $2,222.22.
learn more about Simple interest formula:-
https://brainly.com/question/25845758
#SPJ4
If S={a,b,c} with P(a)=2P(b)=3P(c), find P(a). 9. If S={a,b,c,d,e,f} with P(a)=P(b)=P(c) and P(d)=P(e)=P(f)=0.1, find P(a). 10. If S={a,b,c,d,e,f} with P(a)=P(b)=P(c), P(d)=P(e)=P(f), and P(d)=2P(a), find P(a). 11. If E and F are two disjoint events in S with P(E)= 0.2 and P(F)=0.4, find P(E∪F),P(E
c
), and P(E∩F). 12. Why is it not possible for E and F to be two disjoint events in S with P(E)=0.5 and P(F)=0.7? 13. If E and F are two disjoint events in S with P(E)= 0.4 and P(F)=0.3, find P(E∪F),P(F
c
),P(E∩F), P((E∪F)
c
), and P((E∩F)
c
). 14. Why is it not possible for S={a,b,c} with P(a)= 0.3,P(b)=0.4, and P(c)=0.5 ?
Answers
Since the total probability of the sample space S must be equal to 1, it is not possible for three events with probabilities that add up to more than 1 to form the sample space.
9. If S={a,b,c,d,e,f} with P(a)=P(b)=P(c) and P(d)=P(e)=P(f)=0.1, find P(a).
Since P(a), P(b), and P(c) are equal, we can let P(a) = P(b) = P(c) = x.
Then, we know that P(d) = P(e) = P(f) = 0.1.
The total probability of the sample space S is equal to 1. So, we can write the equation:
P(a) + P(b) + P(c) + P(d) + P(e) + P(f) = 1
Substituting the given values, we get:
3x + 0.1 + 0.1 + 0.1 = 1
3x + 0.3 = 1
3x = 1 - 0.3
3x = 0.7
Dividing both sides by 3, we find:
x = 0.7/3
So, P(a) = 0.233.
10. If S={a,b,c,d,e,f} with P(a)=P(b)=P(c), P(d)=P(e)=P(f), and P(d)=2P(a), find P(a).
Let P(a) = P(b) = P(c) = x. And let P(d) = P(e) = P(f) = y.
We also know that P(d) = 2P(a).
Using the equation for the total probability:
P(a) + P(b) + P(c) + P(d) + P(e) + P(f) = 1
We can substitute the given values:
3x + 3y = 1
We also know that P(d) = 2P(a):
y = 2x
Substituting this into the previous equation:
3x + 3(2x) = 1
3x + 6x = 1
9x = 1
Dividing both sides by 9, we find:
x = 1/9
So, P(a) = P(b) = P(c) = 1/9.
11. If E and F are two disjoint events in S with P(E)=0.2 and P(F)=0.4, find P(E∪F), P(Ec), and P(E∩F).
Since E and F are disjoint, their intersection, E∩F, is empty.
The probability of the union of two disjoint events is the sum of their individual probabilities:
P(E∪F) = P(E) + P(F) = 0.2 + 0.4 = 0.6
The complement of E, Ec, is the event that consists of all outcomes in S that are not in E.
The complement of an event has a probability equal to 1 minus the probability of the event:
P(Ec) = 1 - P(E) = 1 - 0.2 = 0.8
Since E and F are disjoint, their intersection, E∩F, is empty, so its probability is 0:
P(E∩F) = 0
12. It is not possible for E and F to be two disjoint events in S with P(E)=0.5 and P(F)=0.7 because the sum of their probabilities would exceed 1.
Since the total probability of the sample space S must be equal to 1, it is not possible for two events with probabilities that add up to more than 1 to be disjoint.
13. If E and F are two disjoint events in S with P(E)=0.4 and P(F)=0.3, find P(E∪F), P(Fc), P(E∩F), P((E∪F)c), and P((E∩F)c).
Since E and F are disjoint, their intersection, E∩F, is empty.
The probability of the union of two disjoint events is the sum of their individual probabilities:
P(E∪F) = P(E) + P(F) = 0.4 + 0.3 = 0.7
The complement of F, Fc, is the event that consists of all outcomes in S that are not in F.
The complement of an event has a probability equal to 1 minus the probability of the event:
P(Fc) = 1 - P(F)
= 1 - 0.3
= 0.7
Since E and F are disjoint, their intersection, E∩F, is empty, so its probability is 0:
P(E∩F) = 0
The complement of the union of two events, (E∪F)c, is the event that consists of all outcomes in S that are not in the union of E and F.
The complement of an event has a probability equal to 1 minus the probability of the event:
P((E∪F)c) = 1 - P(E∪F) = 1 - 0.7 = 0.3
The complement of the intersection of two events, (E∩F)c, is the event that consists of all outcomes in S that are not in the intersection of E and F.
The complement of an event has a probability equal to 1 minus the probability of the event:
P((E∩F)c) = 1 - P(E∩F) = 1 - 0 = 1
14. It is not possible for S={a,b,c} with P(a)=0.3, P(b)=0.4, and P(c)=0.5 because the sum of their probabilities exceeds 1.
Since the total probability of the sample space S must be equal to 1, it is not possible for three events with probabilities that add up to more than 1 to form the sample space.
To know more about probability visit:
https://brainly.com/question/31828911
#SPJ11
eamed $448 at an interest rate of 2.8% after
10 years
Answers
The initial deposit into the account was approximately $319.17.
What is simple interest?Simple interest is a method of calculating the interest charge. Simple interest can be calculated as the product of principal amount, rate and time period.
Simple Interest = (Principal × Rate × Time) / 100
We are given that;
Amount = $448
Rate=2.8%
Time= 10 years
Now,
We can use the formula for compound interest to solve this problem:
A = P(1 + r/n)^(nt)
where:
A = the amount of money in the account after 10 years
Substituting these values into the formula, we get:
$448 = P(1 + 0.028/1)^(1*10)
Simplifying, we get:
$448 = P(1.028)^10
Dividing both sides by (1.028)^10, we get:
P = $448 / (1.028)^10
Using a calculator, we get:
P ≈ $319.17
Therefore, by the given interest answer will be approximately $319.17.
Learn more about simple interest here;
https://brainly.com/question/1548909
#SPJ1
The complete question is;
Find the initial deposit into an account that eamed $448 at an interest rate of 2.8% after 10 years.
A manufacturer of widgets finds that the production cost, What is the selling price per widget as a function of the
C, in dollars per unit is a function of the number of number of widgets produced, and what should the
widgets produced. The selling price, S, of each widget in selling price be if 15 widgets are produced?
dollars is a function of the production cost per unit
C(x) = -0.1x2 + 100
O C(S(x)) = -0.196x2 + 100, $108.64
S(C) = 1.40
O C(S(x) = -0.196x2 + 100; $55.90
O S(C(x)) = -0.14x2 + 140; $144.41
O S(C(x)) = -0.14x2 + 140, $108.50
Answers
Answer:
S(C(x)) = –0.14x2 + 140; $108.50
Step-by-step explanation:
did the assignment
Answer:
DS(C(x)) = -0.14x2 + 140, $108.50

Sonya walks on a treadmill at a constant rate of 3.5 miles per hour. A graph showing the relationship between the time she walks and the distance she travels passes through the origin and through the point (1, 3.5). Name three other points that lie on the graph.
Answers
The other two points on the line are (2, 7) and (4, 14).
What is the slope?The slope is the rate of change of the y-axis with respect to the x-axis.
The equation of a line in slope-intercept form is y = mx + b, where
slope = m and y-intercept = b.
We know the greater the absolute value of a slope is the more steeper is it's graph or rate of change is large.
Given, Sonya walks on a treadmill at a constant rate of 3.5 miles per hour
it is the slope.
∴ The equation of this line passing through point (1, 3.5) is,
3.5 = 3.5(1) + b.
b = 0.
So, y = 3.5x.
Now the other points can be obtained by choosing some integer values of x.
When x = 2, y = 7 ⇒ (2, 7).
When x = 4, y = 14 ⇒ (4, 14).
learn more about lines and slopes here :
https://brainly.com/question/16180119
#SPJ1
Yana, Josh, and Katrina are standing at the vertices of a right triangle as they throw a frisbee. Yana and Josh are standing 18 feet apart, Josh and Katrina are standing 12 feet apart, and Katrina and Yana are standing 9 feet apart. Trae joins the game and stands between Josh and Katrina. What is the shortest possible distance between Trae and Katrina?
Answers
The shortest possible distance between Trae and Katrina is 6 feet.
Since Yana, Josh, and Katrina are standing at the vertices of a right triangle, the distance between Yana and Josh is the hypotenuse of the triangle and the other two sides are the legs.
Pythagoras theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides“.
Using the Pythagorean theorem, we can calculate that the distance between Yana and Katrina is 15 feet.
( 18^2 + 12^2 = 15^2)
Since Trae is standing between Josh and Katrina, the shortest possible distance between Trae and Katrina is half of the distance between Josh and Katrina, which is 6 feet.
To learn more about Pythagorean theorem visit: brainly.com/question/343682
#SPJ4