Enter equations one at a time in order to send a line
through the coins to "capture" them.

Answers
Answer:
y=9x+7
Step-by-step explanation:
Answer:
x=4
Step-by-step explanation:
The line is a straight line going through the x-axis, so the equation will be x=_. Since it goes through (4,0), the answer will be x=4.
Related Questions
Square
G
(x²-8)
meters
x meters
*.
...
What expression represents the total area of the
shaded figure. Simplify your expression.

Answers
The total area of the shaded portion is (x² - 16)(x²- 1) square meters.
What is a square?Square is a regular quadrilateral, which has all the four sides of equal length and all four angles are also equal. The angles of the square are at right-angle or equal to 90-degrees. Also, the diagonals of the square are equal and bisect each other at 90 degrees.
Equation:The area of the outer square is (x² - 8)², and the area of the inner square is x². Therefore, the area of the shaded region can be found by subtracting the area of the inner square from the area of the outer square:
Area of shaded region = Area of outer square - Area of inner square
= (x² - 8)² - x²
Expanding the first term using the formula for the square of a binomial, we get:
Area of shaded region = (x⁴ - 16x² + 64) - x²
= x⁴ - 17x² + 64
Therefore, the expression that represents the total area of the shaded figure is x⁴ - 17x² + 64, which can be simplified by factoring:
x⁴ - 17x² + 64 = (x² - 16)(x² - 1)
So the simplified expression for the total area of the shaded figure is (x² - 16)(x²- 1).
To know more about square, click here
https://brainly.com/question/14198272
#SPJ1
Help pls
Stuck on this question

Answers
Answer:
x = 35
Step-by-step explanation:
since the figures are similar then the ratios of corresponding parts are in proportion, that is
\(\frac{x}{10}\) = \(\frac{14}{4}\) = \(\frac{7}{2}\) ( cross- multiply )
2x = 7 × 10 = 70 ( divide both sides by 2 )
x = 35
A 984-foot tree has grown at a constant rate each year. In the equation below, t is the age of the tree in years.
24t = 984
What is the unit rate in the equation above?
A.
24 feet per year
B.
41 feet per year
C.
984 feet per year
D.
960 feet per year
Answers
The unit rate of 24t = 98 is A. 24 feet per year.
What is unit rate?Unit rate is the rate of increase or decrease of a unit of item
Now, since a 984-foot tree has grown at a constant rate each year. Since we have the equation 24t = 984, wheret is the age of the tree in years.
To determine the unit rate, we compare it with the function y = mx where m = gradient
Now, the gradient is the rate of change of y per unit of x.
Now, comparing y = mx with 24t = 984,
y = 984, m = 24 and t = xSince m = 24 which is the gradient which is also the unit rate.
So, the unit rate of 24t = 98 is A. 24 feet per year.
Learn more about unit rate here:
https://brainly.com/question/29337674
#SPJ1
What is the resulting integral?

Answers
Answer:
\(\displaystyle \int {\frac{2}{(1 + \sqrt{x})^5}} \, dx = \frac{-(4\sqrt{x} + 1)}{3(\sqrt{x} + 1)^4} + C\)
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
BracketsParenthesisExponentsMultiplicationDivisionAdditionSubtractionLeft to RightAlgebra I
Exponential Rule [Root Rewrite]: \(\displaystyle \sqrt[n]{x} = x^{\frac{1}{n}}\)Exponential Rule [Rewrite]: \(\displaystyle b^{-m} = \frac{1}{b^m}\)Calculus
Derivatives
Derivative Notation
Basic Power Rule:
f(x) = cxⁿf’(x) = c·nxⁿ⁻¹Antiderivatives - Integrals
Integration Constant C
U-Substitution
U-SolveIntegration Rule [Reverse Power Rule]: \(\displaystyle \int {x^n} \, dx = \frac{x^{n + 1}}{n + 1} + C\)
Integration Property [Multiplied Constant]: \(\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx\)
Integration Property [Addition/Subtraction]: \(\displaystyle \int {[f(x) \pm g(x)]} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx\)
Step-by-step explanation:
Step 1: Define
\(\displaystyle \int {\frac{2}{(1 + \sqrt{x})^5}} \, dx\)
Step 2: Identify Variables
Find the variables u-solve using u-substitution.
U-Substitution
\(\displaystyle u = 1 + \sqrt{x}\)
\(\displaystyle du = \frac{1}{2\sqrt{x}}dx\)
U-Solve
\(\displaystyle x = (u - 1)^2\)
\(\displaystyle dx = 2\sqrt{x}du\)
Step 3: Integration
[Integral] Rewrite [Integration Property - Multiplied Constant]: \(\displaystyle 2\int {\frac{1}{(1 + \sqrt{x})^5}} \, dx\)[Integral] U-Solve: \(\displaystyle 2\int {\frac{1}{(1 + \sqrt{(u - 1)^2})^5}} \, 2\sqrt{x}du\)[Integral] Simplify: \(\displaystyle 2\int {\frac{2\sqrt{x}}{u^5}} \, du\)[Integral] Rewrite [Integration Property - Multiplied Constant]: \(\displaystyle 4\int {\frac{\sqrt{x}}{u^5}} \, du\)[Integral] U-Solve: \(\displaystyle 4\int {\frac{\sqrt{(u - 1)^2}}{u^5}} \, du\)[Integral] Simplify: \(\displaystyle 4\int {\frac{u - 1}{u^5}} \, du\)[Integral] Rewrite [Integration Property - Subtraction]: \(\displaystyle 4[\int {\frac{u}{u^5}} \, du - \int {\frac{1}{u^5}} \, du]\)[Integrals] Simplify: \(\displaystyle 4[\int {\frac{1}{u^4}} \, du - \int {\frac{1}{u^5}} \, du]\)[Integrals] Rewrite [Exponential Rule - Rewrite]: \(\displaystyle 4[\int {u^{-4}} \, du - \int {u^{-5}} \, du]\)[Integrals] Reverse Power Rule: \(\displaystyle 4[\frac{u^{-3}}{-3} - \frac{u^{-4}}{-4}] + C\)Rewrite [Exponential Rule - Rewrite]: \(\displaystyle 4[\frac{-1}{3u^3} + \frac{1}{4u^4}] + C\)[Brackets] Multiply: \(\displaystyle \frac{-4}{3u^3} + \frac{4}{4u^4} + C\)Back-Substitute: \(\displaystyle \frac{-4}{3(1 + \sqrt{x})^3} + \frac{4}{4(1 + \sqrt{x})^4} + C\)Combine: \(\displaystyle \frac{-(4\sqrt{x} + 1)}{3(\sqrt{x} + 1)^4} + C\)Topic: AP Calculus AB/BC (Calculus I/II)
Unit: Integration
Book: College Calculus 10e
x/2 - 1 = 3
What is X
Answers
Answer:
8
Step-by-step explanation:
x /2 -1 = 3
add 1 to both sides
x/2 = 4
multiply by 2
x = 8
Determine whether or not each of the following continuous-time signals is periodic. If the signal is periodic, determine its fundamental period. (a) x(t) 3 cos(4t (c) x(t) = [cos(2t--)]2 (d) x(t) &'{cos(4m)u(t)} + 풀) (b) x(t) e/m-I)
Answers
The signal, (a) x(t) = 3cos(4t) is periodic with period T = pi/2. To see this, we can compute:
x (t + T) = 3cos (4(t + pi/2)) = 3cos (4t + 2pi) = 3cos(4t)
which shows that the signal repeats itself every T = pi/2 seconds.
\((b) \times (t) = e^{( - t)} \)
This signal is not periodic.
\(e^{(-t)} = e^{(-(t+T))} \)
for all t.
However, this is not possible since e^(-t) approaches 0 as t approaches infinity. Therefore, the signal is not periodic.
\((c) \times (t) = [cos (2t - \frac{\pi}{3}] ^2\)
This signal is periodic with period T = pi. To see this, we can compute:
\(x (t + T) = [cos (2(t + \pi) - \pi/3)] ^2 = [cos (2t + 5\pi/3)] ^2 = [cos (2t - pi/3)] ^2 = x(t) \\
(d) x(t) = cos(4t) u(t) + sin(4t) u(-t)\)
This signal is not periodic. To see this, suppose that there exists a period T such that x(t) = x (t + T) for all t. Then we must have:
cos(4t) u(t) + sin(4t) u(-t) = cos(4(t+T)) u(t+T) + sin(4(t+T)) u(-(t+T)) for all t.
However, this is not possible since the two terms on the left-hand side have different signs for t < 0, whereas the two terms on the right-hand side have the same sign for t < -T.
Therefore, the signal is not periodic.
To know more about Periodic:
brainly.com/question/30426575
#SPJ4
What is the value of the expression 2/5m−1/3 when m = 3?
1/15
13/15
23/15
I don't know.
Answers
Answer:
13/15
Step-by-step explanation:
i took the test :)
simplify that expression
6 (7x + 9)
Answers
can someone help answer this and explain how you did it

Answers
Answer:
2
Step-by-step explanation:
You want the slope of segment DC given points A, B, C, D are collinear and the rise between B and A is 2 units, while the run is 1 unit.
Slope of a lineThe slope of a line is the same everywhere on the line. It is the same for segment DC as for segment BA on the same line.
slope = rise/run = 2/1 = 2
The slope of DC is 2.
<95141404393>
Thanks for reposting the pertinent question:
Therefore the SLOPE of DC:
DC = 2
Step-by-step explanation: Cheers to the person who has explained and answered the question correctly as well.Make a Plan: FORMULA FOR SLOPE OF A LINE: m = rise/run = y1 - y2 / x2 - x1POINTS: D, C, B, and A are COLLINEAR
Now, We can FIND That:SLOPE of: DC is Equal (=) To the SLOPE of: AB
So, Now, The SLOPE of AB:AB = 2/1 = 2
Now, we conclude that:Therefore the SLOPE of DC:
DC = 2
I hope this helps you!
can you please help and explain how to do this

Answers
Answer:
x = -3
Step-by-step explanation:
Notice that the addition of angle <CDH plus angle <HDE have to give the measure of angle <CDE (which is 144 degrees as stated in the problem)
Then, we can say in equation form:
<CDH + <HDE = 144
replacing with their expressions in terms of x:
x + 93 + 57 + x = 144
solving for x:
2 x + 150 = 144
2 x = 144 - 150
2 x = - 6
x = -3
Solve these equations. |x+1/2|=3 2/3
Answers
Answer:
Step-by-step explanation:
|x+a|=b
x+a=±b
x=a±b
x=a+b
and x=a-b
There is 500 mg of potassium in 1 cup (240 ml) of orange juice. Your renal patient must watch his potassium intake not to exceed 2 mg per kg of body weight per day from Orange juice alone. How much juice (in ml) can this patient have per day if the patient weighs 135 lb?
Answers
Answer:
58.79 mL of juice
Step-by-step explanation:
To do this, let's gather the data first:
In 1 cup of orange juice we have 500 mg of potassium. A patient weights 135 lb, and he needs to take care of it's potassium intake and not exceed 2 mg of K / kg per day.
So obviously he cannot drink a whole cup of orange juice. It has to be less. In order to know this, we need to know first the weight in kg. 1 lb equals 0.4536 kg so in 135 lb:
W = 135 lb * 0.4536 kg/lb = 61.24 kg
Now, we need to know with this weight, how much potassium it can takes:
Intake = 61.24 kg * 2 mg/kg = 122.48 mg of K
So, the maximum amount of potassium per day is 122.48 mg. This means that the quantity of orange juice this person can take is:
Juice = 122.48 mg * 240 mL / 500 mg
Juice = 58.79 mL of juice or simply 59 mL
In a sample of 560 adults, 336 had children. Construct a 95% confidence interval for the true population proportion of adults with children.
Give your answers as decimals, to three places
< p <
What is the expected value of �?
Answers
The confidence interval is 0.559 < p < 0.641 and expected value is 0.600
Confidence IntervalTo construct a confidence interval for the true population proportion, we can use the formula:
p ± Z * √((p × (1 - p)) / n)
Where:
p = sample proportion (336/560)
Z = critical value for the desired confidence level
95% confidence = Z-value of approximately 1.96
n = 560
Let's calculate the confidence interval:
p = 336/560 ≈ 0.600
Z ≈ 1.96 (for a 95% confidence level)
n = 560
Plugging these values into the formula:
p ± Z × √((p × (1 - p)) / n)
0.600 ± 1.96 × √((0.600 × (1 - 0.600)) / 560)
0.600 ± 1.96 × √((0.240) / 560)
0.600 ± 1.96 × √(0.0004285714)
0.600 ± 1.96 × 0.020709611
0.600 ± 0.040564459
The confidence interval is:
0.559 < p < 0.641
Therefore, the 95% confidence interval for the true population proportion of adults with children is 0.559 < p < 0.641.
The expected valueFor proportions, the expected value is simply the sample proportion, which is approximately 0.600.
Learn more on confidence interval: https://brainly.com/question/15712887
#SPJ1
2. (5 × 2 + 20/2) + (10 x 2/2 + 5) =
a. 35
b. 42
c. 103
Answers
Answer:
a.35
Step-by-step explanation:
10 + 20/2 equals 20
20/2+5 equals 15
20+15 equals 35
Find the area of the trapezoid.
14 mm
15 mm
36 mm
1. 270 mm²
2. 375 mm²
3. 750 mm²
5. 3780 mm²
Answers
Answer: no one cares
Step-by-step explanation:
because it's to hard\(\pi \pi \pi \pi \pi \pi \pi \pi \pi \pi \pi \pi \pi \left \{ {{y=2} \atop {x=2}} \right. x_{123} \left \{ {{y=2} \atop {x=2}} \right. \lim_{n \to \infty} a_n \int\limits^a_b {x} \, dx \left \{ {{y=2} \atop {x=2}} \right. \sqrt{x} \sqrt{x} \sqrt{x} \alpha \pi x^{2} x^{2} x^{2} \\ \\ \neq \pi \pi 5069967.94389438.494898 that's the answer\)A teaching hospital in South-West Part of Nigeria receives on the average 5 pregnant women with high blood pressure per week. What is the probability that on a particular week, the teaching hospital will receive:
1.) No high BP pregnant woman
Answers
Answer:
The probability that on a particular week, the hospital will receive on high BP pregnant woman is 0.0068
Step-by-step explanation:
We use the Exponential distribution,
Since we are given that on average, 5 pregnant women with high blood pressure come per week,
So, average = m = 5
Now, on average, 5 people come every week, so,
5 women per week,
so, we get 1 woman per (1/5)th week,
Hence, the mean is m = 1/5 for a woman arriving
and λ = 1/m = 5 = λ
we have to find the probability that it takes higher than a week for a high BP pregnant woman to arrive, i.e,
P(X>1) i.e. the probability that it takes more than a week for a high BP pregnant woman to show up,
Now,
P(X>1) = 1 - P(X<1),
Now, the probability density function is,
\(f(x) = \lambda e^{-\lambda x}\)
And the cumulative distribution function (CDF) is,
\(CDF = 1 - e^{-\lambda x}\)
Now, CDF gives the probability of an event occuring within a given time,
so, for 1 week, we have x = 1, and λ = 5, which gives,
P(X<1) = CDF,
so,
\(P(X < 1)=CDF = 1 - e^{-\lambda x}\\P(X < 1)=1-e^{-5(1)}\\P(X < 1)=1-e^{-5}\\P(X < 1) = 1 - 6.738*10^{-3}\\P(X < 1) = 0.9932\\And,\\P(X > 1) = 1 - 0.9932\\P(X > 1) = 6.8*10^{-3}\\P(X > 1) = 0.0068\)
So, the probability that on a particular week, the hospital will receive on high BP pregnant woman is 0.0068
expand and simplify (x+5)(x-1)
Answers
The expanded and simplified form of the expression (x + 5)(x - 1) is x² - x + 5x - 5.
What is the expanded form of the expression?Given the expression in the question;
(x + 5)(x - 1)
To expand and simplify the expression (x+5)(x-1),
we use the distributive property:
(x + 5)(x - 1)
x(x - 1) + 5(x - 1)
Now we can simplify each term by using the distributive property again:
x(x - 1) = x² - x
5(x - 1) = 5x - 5
Putting these terms back together, we have:
(x+5)(x-1) = x² - x + 5x - 5
Combining like terms, we get:
(x+5)(x-1) = x² + 4x - 5
Therefore, (x+5)(x-1) simplifies to the quadratic expression x² + 4x - 5.
Learn more about distributive property here: https://brainly.com/question/13130806
#SPJ1
suppose a random sample of 40 houses are selected from the city. estimate the probability that the mean value of the 40 houses is less than $500,000 . show your work
Answers
a. Thus, the probability that a randomly selected house has a value less than $500,000 is 0.71
b. the probability that the mean value of the 40 houses is less than $500,000 is 0.9863
a. The mean of the distribution is given as $403,000 and the standard deviation is $278,000.
To estimate the probability that a randomly selected house has a value less than $500,000:
P( x < 500,000)=P(x=0)+P(x=500)
=0.34+0.37+
=0.71
Thus, the probability that a randomly selected house has a value less than $500,000 is 0.71
b. -since 40 is larger than or equal to 30, we assume a normal distribution.
-The probability can therefore be calculated as:
P(x')=P( z < (x' -u)/σ.sqrt(n)))
P(z< (500-403)/(578sqrt(40)))
=P(z<2.2068)
=0.986336
Hence, the probability that the mean value of the 40 houses is less than $500,000 is 0.9863
The complete question is -
a) Suppose one house from the city will be selected at random. Use the histogram to estimate the probability that the selected house is valued at less than $500,000. Show your work.
(b) Suppose a random sample of 40 houses are selected from the city. Estimate the probability that the mean value of the 40 houses is less than $500,000. Show your work.
learn more about probability,
https://brainly.com/question/30034780
#SPJ4

55 POINTS QUICK PLS Your friend is able to invest $120 a month in a 401(k) with a predicted growth rate of 3%. Your friend's company will match 50% of your friend's contributions.

Answers
a. The monthly contribution from a friend's company is $120 minus 0.5, or $60.
b. The total monthly contribution to the fund is $180.
The computation of FV in Excel is shown in the attachment below:
What is meant by growth rate?Using the current number as a starting point, subtract the prior value to determine the growth rate. To calculate the growth rate in percentage terms, divide the difference by the previous amount and multiply the result by 100. Growth Rate equals (Ending Value - Beginning Value) - 1. The year-over-year (YoY) growth rate of a business, for instance, would be 20% if its revenue increased from $100 million in 2020 to $120 million in 2021.
GDP, turnover, wages, etc., all have growth rates that reflect how much they have changed over time (month, quarter, year). Percentages are a pretty common way to communicate it.
20 years is the age.
20 times 12 periods equals 240.
3% growth rate
The computation of FV in Excel is shown in the attachment below:
So, FV= $7,223,115.77
To know more about growth rate, visit:
https://brainly.com/question/11743945
#SPJ1

Can someone pls answer this because I only got 30 min with like 25 questions left

Answers
That’s really it
SOMEONE PLEASE HELP ASAPPPPPPP

Answers
Answer:
z/17
Step-by-step explanation:
ratio means divide
z/17
factorize:4(a+b)-x²(a+b)
Answers
Step-by-step explanation:
\(4(a + b) - {x}^{2} (a + b)\)
\(a + b(4 - {x}^{2} )\)
\((a + b)(2 - x)(2 + x)\)
Fill in the missing statements and reasons for the proof. Given ∠2 ≅ ∠3 proof ∠1 ≅ ∠4
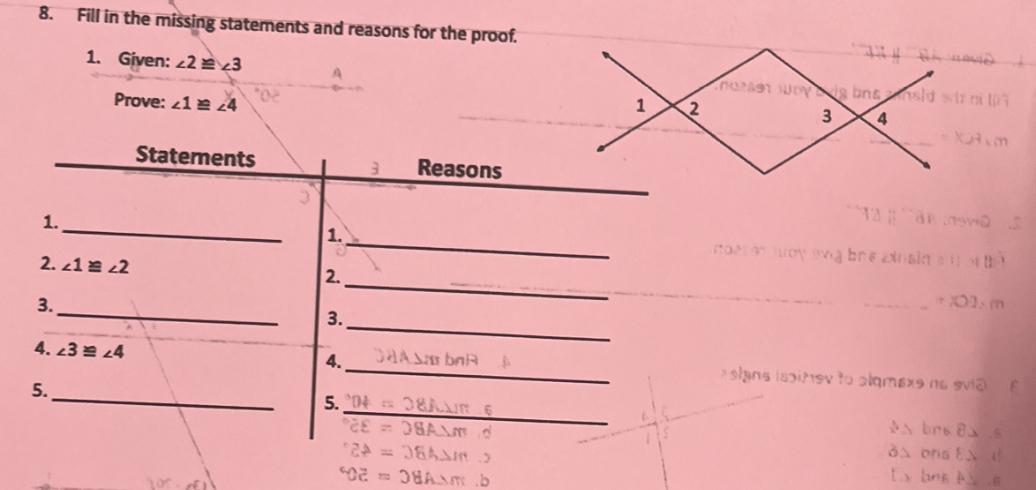
Answers
The proof is given as follows:
∠1 ≅ ∠2 - Vertical Angles are ≅∠2 ≅ 3 - Given∠3 ≅4 - Vertical Angles are ≅Thus, ∠1 ≅ 4 Transitive properties.What are transitive properties?The transitive property argues that "if two quantities are equal to the third quantity, then we may claim that all the quantities are equal to one other".
The term transitive refers to a transfer. If there are three quantities a, b, and c, and if an is connected to b by some rule and b is related to c by the same method, then a and c are related to each other by the same rule; this property is known as the transitive property of equality.
Learn more about vertical angles:
https://brainly.com/question/10668231
#SPJ1
What is the equation in slope-intercept form of the line that passes through the points (-4, 2) and (12, 6) ?
The possible answers are
y=0.25x +3
y=0.25x - 4.5
y=4x + 18
y=4x - 42
Answers
Today only, a table is being sold for $475. This is 76% of its regular price. What was the price yesterday?
Answers
Answer:
625
Step-by-step explanation:
0.76x=475
x=625
Hope I helped!
HELPPPPPPPPPPPPPPPPPPPPPPPPPPPHEL

Answers
Answer:
15 degrees
Step-by-step explanation:
90-75= 15
........
Are the two triangles similar? If so, state the reason and the similarity statement.

Answers
Answer:
C :)
Step-by-step explanation:
No, the two triangles are similar. Option D is correct.
What is the similarity law for triangles?While having the same size is not required, it is required by law to demonstrate that the two triangles have the same form. The angles that correspond to those sides have the same congruence and the same ratio of sides.
It is given in ΔVWX and ΔYZX
WX=8,ZX=2
VX=9,YX=3
When two triangles have an equal number of corresponding sides and corresponding angles, they are said to be similar.
It is obtained that,
ZX/WX=1:4
YX/VX=1:3
ZX/WX≠YX/VX
Since their ratio is not equal there is no possibility for the triangles to be similar. As a result, the triangle is not similar.
Thus, option D is correct.
Learn more about the similarity of triangles here:
brainly.com/question/8045819
#SPJ2
A cylinder open on both ends has a diameter of 10 decimeters(dm) and a height of 10 decimeters(dm). What is the
surface area of the cylinder?
314 dm ²
471 dm ²
628 dm ²
157dm2
Answers
the surface area of the cylinder is approximately 471 dm².
Now, For the surface area of the cylinder, we need to find the lateral area and the area of the two circular bases.
Since, The formula for the lateral area of a cylinder is
L = 2πrh,
where r is the radius of the cylinder and h is the height.
In this case, the diameter is 10 dm,
So the radius is 5 dm.
And the height is also 10 dm.
Therefore, the lateral area is:
L = 2πrh
L = 2π(5 dm)(10 dm)
L = 100π dm²
The formula for the area of a circle is
A = πr²,
where r is the radius.
In this case, the radius is 5 dm,
So the area of each base is:
A = πr²
A = π(5 dm)²
A = 25π dm²
To find the total surface area, we add the lateral area and the area of the two bases:
SA = 2(Area of Base) + Lateral Area
SA = 2(25π dm²) + 100π dm²
SA = 50π dm² + 100π dm²
SA = 150π dm²
Substitute pi as 3.14, we can calculate:
SA ≈ 150(3.14) dm²
SA ≈ 471 dm²
Therefore, the surface area of the cylinder is approximately 471 dm².
To learn more about cylinder visit:
https://brainly.com/question/30317329
#SPJ1
How many millimeters in 6.5 centimeters
Answers
Answer:
65 mil in 6.5 centimeters
Step-by-step explanation:
Answer:
There are 65 millimeters in 6.5 cm.
Step-by-step explanation:
For every 1 centimeter, there are 10 millimeters.
What must be true with the attached image question

Answers
The true statement is B.
The function will have at least one zero on the interval -5 < x < 4
What must be true?Here we have a polynomial function g(x), and we know that it passes through two known points (-5, 6) and (4, -3).
Remember that a relation is only a function if each point on its domain is mapped into a single point in the range.
Also, this is a polynomial function, so it is continuous, then there are no jumps.
Notice that on the first point the y-value is positive.The second point has a negative y-value.So, at some point in that interval x ∈ (-5, 4), we must have a zero for our function, where a zero is a value of x such that:
g(x)= 0
Then the correct statement is B, g(x) has at least one zero i the given interval.
Learn more about polynomial functions:
https://brainly.com/question/7693326
#SPJ1