4. Find the convolution of sinc(4t) and sinc(pi*t)
Answers
The convolution of sinc(4t) and sinc(pi*t) can be expressed as a function of t that combines the properties of both sinc functions.
The resulting function exhibits periodic behavior and its shape is determined by the interaction between the two sinc functions. The convolution of sinc(4t) and sinc(pi*t) is given by: (convolution equation)
To understand this result, let's break it down. The sinc function is defined as sin(x)/x, and sinc(4t) represents a sinc function with a higher frequency. Similarly, sinc(pi*t) represents a sinc function with a lower frequency due to the scaling factor pi.
When these two sinc functions are convolved, the resulting function is periodic with a period determined by the lower frequency sinc function. The convolution operation involves shifting and scaling of the sinc functions, and the interaction between them produces a combined waveform. The resulting waveform will have characteristics of both sinc functions, with the periodicity and frequency content determined by the original sinc functions.
In summary, the convolution of sinc(4t) and sinc(pi*t) yields a periodic waveform with characteristics influenced by both sinc functions. The resulting function combines the properties of the original sinc functions, resulting in a waveform with a specific periodicity and frequency content.
Learn more about sinc functions here:
https://brainly.com/question/26020087
#SPJ11
Related Questions
show that log ab×log ba =1
Answers
Answer:
See below for proof.
Step-by-step explanation:
Given:
\(\log_ab \times \log_ba=1\)
To prove the given equation, begin by changing the base of the two logs so that they have the same base.
\(\boxed{\textsf{Change of base}: \quad \log_pr=\dfrac{\log_xr}{\log_xp}}\)
Change the base of both logs to x by using the change of base formula:
\(\implies \log_ab=\dfrac{\log_xb}{\log_xa}\)
\(\implies \log_ba=\dfrac{\log_xa}{\log_xb}\)
Substitute into the equation:
\(\implies \log_ab \times \log_ba=\dfrac{\log_xb}{\log_xa} \times \dfrac{\log_xa}{\log_xb}\)
\(\textsf{Apply the fraction rule} \quad \dfrac{a}{c}\times \dfrac{b}{d}=\dfrac{a \times b}{c \times d}:\)
\(\implies \dfrac{\log_xb \times \log_xa}{\log_xa \times \log_xb}\)
Apply the commutative property of multiplication to the numerator:
\(\implies \dfrac{\log_xa \times \log_xb}{\log_xa \times \log_xb}\)
Cancel the common factor logₓb:
\(\implies \dfrac{\log_xa}{\log_xa}\)
\(\textsf{Apply the fraction rule} \quad \dfrac{n}{n}=1:\)
\(\implies \dfrac{\log_xa}{\log_xa}=1\)
Hence proving that:
\(\log_ab \times \log_ba=1\)In one calculation:
\(\begin{aligned}\implies \log_ab \times \log_ba & =\dfrac{\log_xb}{\log_xa} \times \dfrac{\log_xa}{\log_xb}\\\\&=\dfrac{\log_xb \times \log_xa}{\log_xa \times \log_xb}\\\\&=\dfrac{\log_xa \times \log_xb}{\log_xa \times \log_xb}\\\\&=\dfrac{\log_xa}{\log_xa}\\\\&=1\end{aligned}\)
What is the answer please show work 7x + 4 = 5x + 10
Answers
Answer:
x=3
Step-by-step explanation:
subtract 5x from 7x
subtract 4 from 10
divide 2x and 6 by 2
Answer:
x=3
Step-by-step explanation:
7x +4 =5x +10
7x - 5x =10 - 4
2x =6
x=6 :2
x=3
7 ×3 +4 =5 ×3 +10
21 +4 =15 +10
25 =25
Where is the graph of f(x)=4[x-3]+2 discontinuos
Answers
Answer:
Below
Step-by-step explanation:
4 [x-3] + 2 = y is not discontinuous anywhere
However 4 / [x-3] + 2 DOES have a discontinuity at x = 3 because this would cause the denominator to be zero <===NOT allowed !!
francine wants to join a health club and has narrowed it down to two choices. the sportshaus charges an initiation fee of $ 500 and $ 10 per month. fitness first has an initiation fee of $ 50 and charges $ 25 month.
Answers
The equation for the total cost for Sports Haus is 500 + 10x and the equation for Fitness First is 50 + 25x .
In the question ,
it is given that ,
Francie wants to join the health Club .
For the Sports Haus the initiation fees = $500
per month charge = $10
let the number of months be= "x" ,
so , the equation to represent the total cost for Sports Haus Club for x months is 500 + 10x .
For the Fitness First the initiation fees = $50
per month charge = $25
so , the equation to represent the total cost for Fitness First Club for x months is 50 + 25x .
Therefore , The equation for the total cost for Sports Haus is 500 + 10x and the equation for Fitness First is 50 + 25x .
The given question is incomplete , the complete question is
Francine wants to join a health club and has narrowed it down to two choices. The Sports Haus charges an initiation fee of $ 500 and $ 10 per month. Fitness First has an initiation fee of $ 50 and charges $ 25 month . write an equation for the total cost of each health club for x months .
Learn more about Equation here
https://brainly.com/question/3016187
#SPJ4
What value of makes the equation 0.25(10x-3)= 1.5(x+2) - 0.75 true?
A. x = 3
B. x= 4
C. x= 3.75
D. x= 4.25
Answers
Answer:
3.75
Step-by-step explanation:
2.5x-.75=1.5x+3
x=3.75
A bolt manufacturer is very concerned about the consistency with which his machines produce bolts. The bolts should be 0.2 centimeters in diameter. The variance of the bolts should be 0.025. A random sample of 15 bolts has an average diameter of 0.21 cm with a standard deviation of 0.1587. Can the manufacturer conclude that the bolts vary by more than the required variance at α=0.01 level? Step 1 of 5: State the hypotheses in terms of the standard deviation. Round the standard deviation to four decimal places when necessary. A bolt manufacturer is very concerned about the consistency with which his machines produce bolts. The bolts should be 0.2 centimeters in diameter. The variance of the bolts should be 0.025. A random sample of 15 bolts has an average diameter of 0.21 cm with a standard deviation of 0.1587. Can the manufacturer conclude that the bolts vary by more than the required variance at α=0.01 level? Step 2 of 5: Determine the critical value(s) of the test statistic. If the test is twotailed, separate the values with a comma. Round your answer to three decimal places. A bolt manufacturer is very concerned about the consistency with which his machines produce boits. The bolts should be 0.2 centimeters in diameter. The variance of the boits should be 0.025. A random sample of 15 bolts has an average diameter of 0.21 cm with a standard deviation of 0.1587. Can the manufacturer conclude that the bolts vary by more than the required variance at α=0.01 level?
Answers
To determine if the bolts vary by more than the required variance, we can conduct a hypothesis test. The null hypothesis (H₀) states that the variance of the bolts is equal to or less than the required variance (σ² ≤ 0.025), while the alternative hypothesis (H₁) states that the variance is greater than the required variance (σ² > 0.025).
Next, we need to determine the critical value(s) of the test statistic. Since we are testing for variance, we will use the chi-square distribution. For a one-tailed test with α = 0.01 and 14 degrees of freedom (n-1), the critical value is 27.488.
Now, we can compare the test statistic to the critical value. The test statistic is calculated as (n-1) * s² / σ², where n is the sample size (15), s² is the sample variance (0.1587²), and σ² is the required variance (0.025).
If the test statistic is greater than the critical value, we reject the null hypothesis and conclude that the bolts vary by more than the required variance. Otherwise, we fail to reject the null hypothesis.
To learn more about Hypothesis test - brainly.com/question/29996729
#SPJ11
To determine if the bolts vary by more than the required variance, we can conduct a hypothesis test. The null hypothesis (H₀) states that the variance of the bolts is equal to or less than the required variance (σ² ≤ 0.025), while the alternative hypothesis (H₁) states that the variance is greater than the required variance (σ² > 0.025).
Next, we need to determine the critical value(s) of the test statistic. Since we are testing for variance, we will use the chi-square distribution. For a one-tailed test with α = 0.01 and 14 degrees of freedom (n-1), the critical value is 27.488.
Now, we can compare the test statistic to the critical value. The test statistic is calculated as (n-1) * s² / σ², where n is the sample size (15), s² is the sample variance (0.1587²), and σ² is the required variance (0.025).
If the test statistic is greater than the critical value, we reject the null hypothesis and conclude that the bolts vary by more than the required variance. Otherwise, we fail to reject the null hypothesis.
To learn more about Hypothesis test - brainly.com/question/29996729
#SPJ11
iq scores have a mean of 100 and standard deviation of 16. sat scores have a mean of 1000 with a standard deviation of 100. which is probably less likely, randomly meeting someone whose IQ is under 80 or someone who obtained a SAT score of over 1150
Answers
It is less likely to randomly meet someone who obtained a SAT score of over 1150.
What is Z score?Z score or standard score is defined as the number of standard deviations by which the observed value is above or below the mean value.
The formula for calculating z score is,
z = (x - μ) / σ
where x is the observed value, μ is the population mean and σ is the population standard deviation.
For IQ scores,
z = (80 - 100) / 16 = -1.25
For SAT scores,
z = (1150 - 1000) / 100 = 150/100 = 1.5
z score is closer to 0 for IQ scores and far to 0 for SAT scores.
Hence it is less likely to meet someone who obtained a SAT score of over 1150.
Learn more about Z score here :
https://brainly.com/question/15016913
#SPJ1
if you borrow $700 for 5 years at an annual interest rate of 7%, how much will you pay altogether?
Answers
Answer:
707 dollars
Step-by-step explanation:
Explanation: $700 x 0.07 = 49 which is for one year multiple this by 5 which gives you $245.00 then add the $700 loan you borrow which give us $945.00 as our total
The real roots for the equation x4 – x3 10x2 – 16x – 96 = 0 are –2 and 3. what are the nonreal solutions? –i, i –2i, 2i –4i, 4i –16i, 16i
Answers
The Non-real solutions for the equation \(x^{4} -x^{3}+10x^{2} -16x-96=0\) are (-4i, 4i).
Non-real solution:
An answer to a mathematical equation with the root of a negative number that cannot be determined using solely real numbers—i.e., numbers that can be described along a single axis—is referred to as a non-real solution.
If a quadratic has a negative discriminant, then the quadratic equation has a Non-real solution.
Given,
\(x^{4} -x^{3}+10x^{2} -16x-96=0\)
On factorizing the above equation, we get
\((x-3)(x-2)(x^{2} +16)=0\)
Applying Zero Product Property,
\(x^{2} +16 = 0\) or \(x-3=0\) 0r \(x+2=0\)
Taking \(x^{2} +16 = 0\), we get
\(x^{2} =-16\)
x = ± \(\sqrt{-16}\)
x = ± 4i [∵ i = √-1]
Hence,
The Non-real solutions for the equation \(x^{4} -x^{3}+10x^{2} -16x-96=0\) are (-4i, 4i).
Learn more about Non-real Solutions here
https://brainly.com/question/27997332
#SPJ4
Answer:
C
Step-by-step explanation:
edge 2026
Please solve this fast

Answers
Answer:
34
Step-by-step explanation:

executive workout dropouts. refer to the journal of sport behavior (2001) study of variety in exercise workouts, presented in exercise 7.130 (p. 343). one group of 40 people varied their exercise routine in workouts, while a second group of 40 exercisers had no set schedule or regulations for their workouts. by the end of the study, 15 people had dropped out of the first exercise group and 23 had dropped out of the second group. a. find the dropout rates (i.e., the percentage of exercisers who had dropped out of the exercise group) for each of the two groups of exercisers. b. find a 90% confidence interval for the difference between the dropout rates of the two groups of exercisers.
Answers
The 90% confidence interval for the difference between the dropout rates of the two groups is (-0.366, -0.034).
a. To find the dropout rates for each group of exercisers, we divide the number of dropouts by the total number of exercisers in each group and multiply by 100 to get a percentage.
For the first exercise group:
Dropout rate = (Number of dropouts / Total number of exercisers) * 100
= (15 / 40) * 100
= 37.5%
For the second exercise group:
Dropout rate = (Number of dropouts / Total number of exercisers) * 100
= (23 / 40) * 100
= 57.5%
b. To find the 90% confidence interval for the difference between the dropout rates of the two groups, we can use the formula:
Confidence Interval = (p1 - p2) ± Z * √[(p1 * (1 - p1) / n1) + (p2 * (1 - p2) / n2)]
where p1 and p2 are the dropout rates of the two groups, n1 and n2 are the respective sample sizes, and Z is the Z-score corresponding to a 90% confidence level.
Using the given information, p1 = 0.375, p2 = 0.575, n1 = n2 = 40, and for a 90% confidence level, the Z-score is approximately 1.645.
Substituting these values into the formula, we have:
Confidence Interval = (0.375 - 0.575) ± 1.645 * √[(0.375 * (1 - 0.375) / 40) + (0.575 * (1 - 0.575) / 40)]
Calculating the values within the square root and simplifying, we get:
Confidence Interval = -0.2 ± 1.645 * √(0.003515 + 0.006675)
= -0.2 ± 1.645 * √0.01019
= -0.2 ± 1.645 * 0.100944
= -0.2 ± 0.166063
know more about 90% confidence interval here:
https://brainly.com/question/29680703
#SPJ11
If the length of the side of a square changes by a factor of 3, by what factor does the area change?
Answers
Answer:
9
Step-by-step explanation:
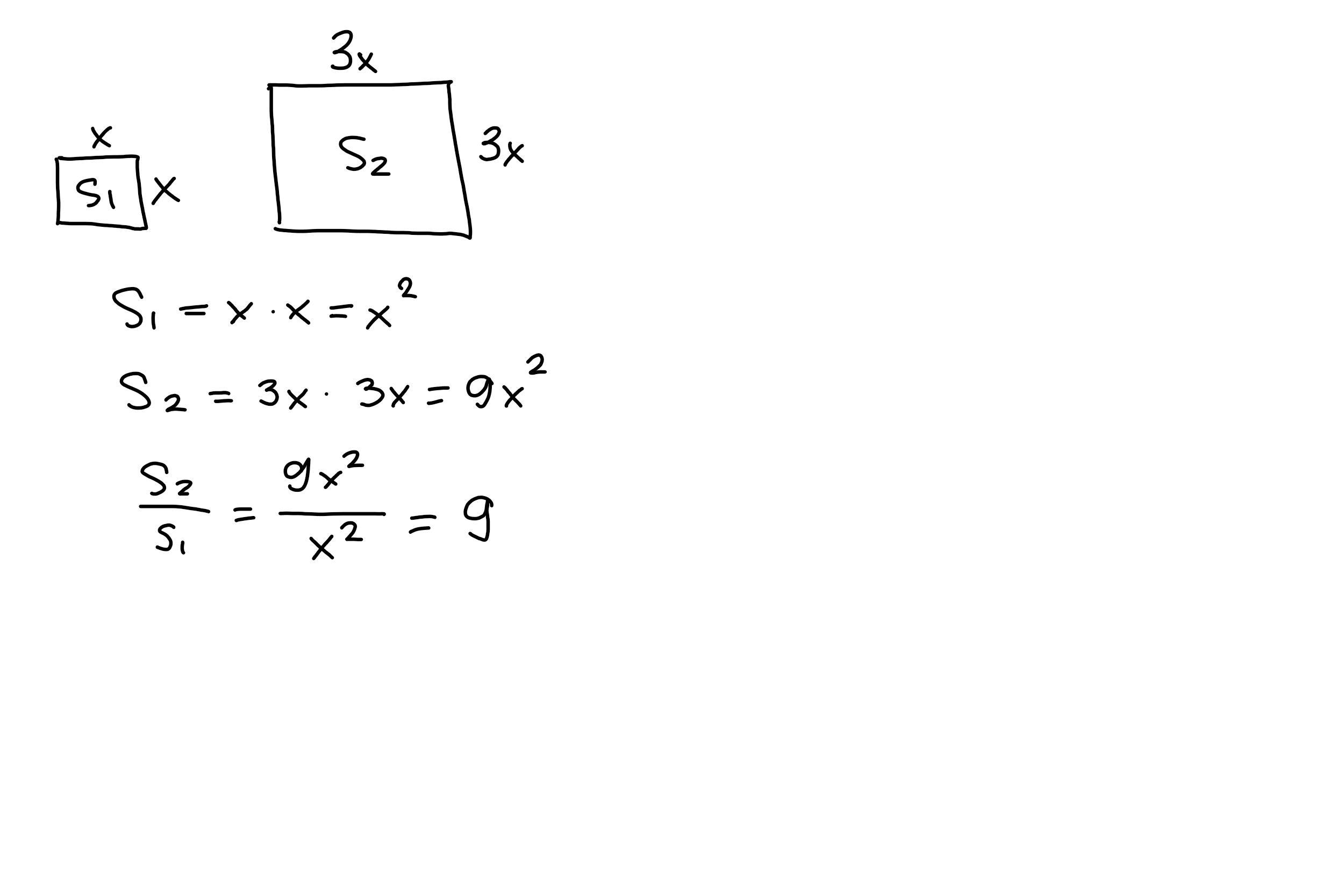
Simplify 4r-4r-10s+2s
Answers
The answer is: −8s
Hope this helps :)
Determine whether the series is convergent or divergent.
1+1/16+1/81+1/256+1/625+....
Answers
To determine if the series 1+1/16+1/81+1/256+1/625+... is convergent or divergent the sum of the series exists and is finite, we can conclude that the series is convergent.
To determine if the series 1+1/16+1/81+1/256+1/625+... is convergent or divergent, we need to apply the convergence tests. The series is a geometric series with a common ratio of 1/4 (each term is one-fourth of the previous term). The formula for the sum of an infinite geometric series is a/(1-r), where a is the first term and r is the common ratio. In this case, a = 1 and r = 1/4.
Using the formula, we get:
sum = 1/(1-1/4) = 1/(3/4) = 4/3
Since the sum of the series exists and is finite, we can conclude that the series is convergent.
To know more about divergent series visit :
https://brainly.com/question/15415793
#SPJ11
The number f of miles a ship is from its destination x hours after starting a voyage is given by f(x) = 80-20x. The number f of miles a submarine is from its destination x hours after leaving port is shown in the graph below. State the distance and length of time if each voyage. The ship traveled ___ miles in __ hours. The submarine traveled __ miles in __ hours.
Answers
The ship traveled 80 miles in 4 hours while the submarine traveled 75 miles in 5 hours.
How to determine the distance and time traveled?Based on the information provided, we can logically deduce that the ship is initially 80 miles away from its destination. Thus, f(x) would be equal to 0, if it traveled 80 miles and 0 miles away from its destination:
f(x) = 80 - 20x
0 = 80 - 20x
20x = 80
x = 80/20
x = 4 hours.
By critically observing the graph (see attachment) for the submarine's voyage, we can logically deduce the following:
Distance = 75 miles.Time = 5 hours.Read more on graphs here: https://brainly.com/question/13511914
#SPJ1

Which two expressions are equivalent?
.3.X+6 and 3. (x+2)
2+(4.x) and (2+4). (2+x)
(x=15)+5 and 5+(15-x)
5.(x-3) and 5.3-5.X
Answers
Answer:
Evaluate x + 23 when x = −14. If you missed this problem, review Example 4.9.15. Evaluate 15 − y when y = −5.
Step-by-step explanation:
Find the value of k if the graph of y=kx passes through the given point.
A(4,-80)
K=?
Answers
The value of k from the equation is k = -20
What is an Equation of a line?The equation of a line is expressed as y = mx + b where m is the slope and b is the y-intercept
And y - y₁ = m ( x - x₁ )
y = y-coordinate of second point
y₁ = y-coordinate of point one
m = slope
x = x-coordinate of second point
x₁ = x-coordinate of point one
The slope m = ( y₂ - y₁ ) / ( x₂ - x₁ )
Given data ,
Let the equation of line be represented as A
Now , the value of A is
y = kx be equation (1)
Let the first point be P ( 4 , -80 )
Substituting the values in the equation , we get
-80 = 4k
Divide by 4 on both sides of the equation , we get
k = - ( 80/4 )
On simplifying the equation , we get
k = -20
Hence , the equation is k = -20
To learn more about equation of line click :
https://brainly.com/question/14200719
#SPJ1
Given f(x, y) = 2y^2+ xy^3 +2e^x, find fy.
fy=6xy + 4y
fy = 4xy + x²y
fy=x²y + 8x^y
fy = 4y + 3xy²
Answers
The value of fy is 4y + 3xy², the correct option is D.
We are given that;
f(x, y) = 2y^2+ xy^3 +2e^x
Now,
A function is an expression, rule, or law that describes the relationship between one variable (the independent variable) and another variable (the dependent variable) (the dependent variable). In mathematics and the physical sciences, functions are indispensable for formulating physical relationships.
To find fy, we need to differentiate f(x, y) with respect to y, treating x as a constant.
The derivative of 2y^2 is 4y, using the power rule.
The derivative of xy^3 is 3xy² + x²y, using the product rule and the chain rule.
The derivative of 2e^x is 0, since it does not depend on y.
So, fy = 4y + 3xy² + x²y
We can simplify this by combining like terms:
fy = 4y + 3xy²
Therefore, by the function the answer will be fy = 4y + 3xy².
Learn more about function here:
https://brainly.com/question/2253924
#SPJ1
the length of the path described by the parametric equations x=cos^3t and y=sin^3t
Answers
The length of the path described by the parametric equations
is 3/2units.
What is the length of the path described by the given parametric equations?We can find the length of the path described by the parametric equations x=cos³t and y=sin³t by using the arc length formula.
The arc length formula for a parametric curve given by:
x=f(t) and y=g(t) is given by:
L = ∫[a,b] √[f'(t)² + g'(t)²] dt
where f'(t) and g'(t) are the derivatives of f(t) and g(t), respectively.
In this case, we have:
x = cos³t, so x' = -3cos²t sin t
y = sin³t, so y' = 3sin²t cos t
Therefore,
f'(t)² + g'(t)² = (-3cos²t sin t)² + (3sin²t cos t)²
= 9(cos⁴t sin²t + sin⁴t cos²t)
= 9(cos²t sin²t)(cos²t + sin²t)
= 9(cos²t sin²t)
Thus, we have:
L = ∫[0,2π] √[f'(t)² + g'(t)²] dt
= ∫[0,2π] √[9(cos²t sin²t)] dt
= 3∫[0,2π] sin t cos t dt
Using the identity sin 2t = 2sin t cos t, we can rewrite the integral as:
L = 3/2 ∫[0,2π] sin 2t dt
Integrating, we get:
L = 3/2 [-1/2 cos 2t] from 0 to 2π
= 3/4 (cos 0 - cos 4π)
= 3/2
Therefore, the length of the path described by the parametric equations x=cos³t and y=sin³t is 3/2 units.
Learn more about Parametric curves
brainly.com/question/15585522
#SPJ11
What is the length of UJ?

Answers
Answer:
the answer is 32
Step-by-step explanation:
divide 64 by 2 to get half of it which is 32 because UJ is half of KJ
hope it helps!!
you draw a single card from a normal deck of cards. what is the probability that it will be a 7?
Answers
The probability of drawing a 7 from a normal deck of cards is 1/13 or approximately 0.0769 (rounded to four decimal places).
A normal deck of cards contains 52 cards, which includes 13 cards in each of the four suits: clubs, diamonds, hearts, and spades. Within each suit, there are cards numbered 2 through 10, plus face cards (jack, queen, king) and an ace.
Since there are four 7's in a deck of cards (one in each suit), the probability of drawing a 7 from a normal deck of cards is simply the ratio of the number of 7's to the total number of cards:
P(7) = 4/52
Simplifying, we get:
P(7) = 1/13
P(7) = 0.0769
It is important to note that the probability of drawing a 7 is independent of any previous draws, assuming the deck is shuffled thoroughly before each draw. That is, the probability of drawing a 7 remains the same whether it is the first card drawn or the tenth card drawn.
To learn more about probability click on,
https://brainly.com/question/14091296
#SPJ4
a. Find and plot the z= -1 trace of this quadric surface. Find trace in the space below.
z = (y/4)^2 – (x/2)^2
b. Find and plot the yz trace (x = 0) of this quadric surface. Find trace in the space below
z = (y/4)^2 – (x/2)^2
Answers
Hence, the yz trace is empty, and there are no points to plot on the yz plane.
To find the z = -1 trace of the quadric surface given by \(z = (y/4)^2 - (x/2)^2\), we substitute z = -1 into the equation and solve for y in terms of x:
\(-1 = (y/4)^2 - (x/2)^2\)
Rearranging the equation, we have:
\((y/4)^2 - (x/2)^2 = -1\)
Multiplying through by -1, we get:
\((x/2)^2 - (y/4)^2 = 1\)
Now, we have the equation of a hyperbola. To find the points on the hyperbola, we can choose different values of x and solve for y.
Let's choose some values of x:
When x = 0, we have:
\((0/2)^2 - (y/4)^2 = 1\\0 - (y/4)^2 = 1\\-(y/4)^2 = 1\)
\((y/4)^2 = -1\)
Therefore, there are no points on the yz trace (x = 0) of this quadric surface.
To know more about points,
https://brainly.com/question/32723813
#SPJ11
a.
Complete the diagram to show the amount of flour and eggs needed for 2, 3, and
4 batches of cookies.
b.
What is the ratio of cups of flour to eggs?
C.
How much flour and how many eggs are used in 4 batches of cookies?
d.
How much flour is used with 6 eggs?
e.
How many eggs are used with 15 cups of flour?
Answers
a. To complete the diagram for 2, 3, and 4 batches of cookies, we need to find the amounts of flour and eggs required for each batch. b. The ratio of cups of flour to eggs can be determined by comparing the amounts needed for a single batch.
c. To find the amounts of flour and eggs used in 4 batches of cookies, we'll multiply the amounts needed for a single batch by 4. d. To determine how much flour is used with 6 eggs, we need to find the proportion of flour to eggs in the original recipe. e. To find how many eggs are used with 15 cups of flour, we need to determine the proportion of eggs to flour in the original recipe.
(assuming 1 batch needs 2 cups of flour and 3 eggs):
a. For 2 batches: 4 cups of flour and 6 eggs; For 3 batches: 6 cups of flour and 9 eggs; For 4 batches: 8 cups of flour and 12 eggs.
b. The ratio of cups of flour to eggs is 2:3.
c. For 4 batches of cookies, you'll need 8 cups of flour and 12 eggs.
d. With 6 eggs, you'll use 4 cups of flour (since the ratio is 2:3, and 6 eggs correspond to 2 times the original recipe).
e. With 15 cups of flour, you'll use 22.5 eggs (since the ratio is 2:3, and 15 cups of flour correspond to 7.5 times the original recipe, but you can't have half an egg, so you may need to adjust the amount of flour or use a different proportion).
To know more about amounts visit :
https://brainly.com/question/16629663
#SPJ11
cual es el resultado de esta operacion urge 27x - 6x
Answers
Answer:
21x
Step-by-step explanation:
No más debes de restar 6 de 27 y obtienes 21 y agregas el x
Which polynomials are in standard form? x2 3x 2 q3 â€"" 15q 12q2 â€"" 16 4a a2 a â€"" 2 3x4 4x3 â€"" 3x2 â€"" 1 3t3 3t2 2t 14 a3 â€"" 6a 8a2
Answers
The polynomials are in standard form is x2 + 3x + 2, 3t3 + 3t2 + 2t 14
The standard form of a polynomial is expressed by writing the highest degree of terms first then the next degree and so on. The standard form of polynomial is given by, f(x) = aₙxⁿ + aₙ₋₁xⁿ⁻¹ + aₙ₋₂xⁿ⁻² .....a₁x + a0, where x is the variable and ai are coefficients.
In the given options, when we analyse
x2 + 3x + 2 is given in standard form that is x2 + 3x + 2
15q 12q2 is not present in standard form
3t3 + 3t2 + 2t 14 is given in standard form
Therefore, the polynomials are in standard form is x2 + 3x + 2, 3t3 + 3t2 + 2t 14
To learn more about polynomials refer here
https://brainly.com/question/4142886
#SPJ4
I bought a new shirt last night that costs 46$. Becasue there was a little stain on it they gave me an 8% discount. How much did i
pay for the shirt
Answers
answer: $42.32
8% = 0.08
0.08 x 46 = 3.68
46 - 3.68 = 42.32
.2. Determine whether the feasible set for each of the following systems of constraints is convex, and if not, indicate points x^1 and x² that violate definition. a) (x1)² + (x2)² > 9
x1 + x2 ,10
x1, x2 > 0
Answers
The feasible set for this system of constraints is not convex, and the points (5, 5) and (3, 7) violate the convexity definition.
To determine whether the feasible set for each system of constraints is convex, we need to analyze the constraints individually and examine their intersection.
a) (x1)² + (x2)² > 9
This constraint represents points outside the circle with a radius of √9 = 3. The feasible set includes all points outside this circle.
b) x1 + x2 ≤ 10
This constraint represents points that lie on or below the line x1 + x2 = 10. The feasible set includes all points on or below this line.
c) x1, x2 > 0
This constraint represents points in the positive quadrant, where both x1 and x2 are greater than zero.
Now, let's analyze the intersection of these constraints:
Considering the first two constraints (a and b), we can see that the feasible set consists of all points outside the circle (constraint a) and below or on the line x1 + x2 = 10 (constraint b).
To determine whether the feasible set is convex, we need to check if any two points within the set create a line segment that lies entirely within the set.
If we consider the points (5, 5) and (3, 7), both points satisfy the individual constraints (a) and (b). However, the line segment connecting these two points, which is the line segment between (5, 5) and (3, 7), exits the feasible set since it passes through the circle (constraint a) and above the line x1 + x2 = 10 (constraint b).
Therefore, the feasible set for this system of constraints is not convex, and the points (5, 5) and (3, 7) violate the convexity definition.
Learn more about circle here
brainly.com/question/11878555
#SPJ4
An ice machine makes 1 pounds of ice every hour. Which graph shows this
proportional relationship?
Pounds of Ice
s of Ice
6
54321
Total Ice Made
0 1 2 3 4 5 6
Number of Hours
6
Total Ice Made
Pounds of Ice
of Ice
65432
Total Ice Made
0 1 2 3 4 5 6
Number of Hours
65
Total Ice Made
Answers
The graph that represents the situation is required.
What is graph?
A graph is a structure that resembles a set of items in discrete mathematics, more especially in graph theory, in which certain pairs of the objects are conceptually "connected." The items are represented by mathematical abstractions known as vertices, and each pair of connected vertices is referred to as an edge.
Graphs are a popular tool for graphically illuminating data connections. A graph serves the objective of presenting facts that are either too many or complex to be fully expressed in the text while taking up less room.
Here the X- axis denotes the number of hours and
Y- axis denotes the pounds of ice.
The given ordered pair is
\(\left(\frac{1}{2}, 1 \frac{1}{2}\right)=(0.5,1.5)\)
At zero hours the ice produced will be zero so, the third and fourth options are incorrect.
The only graph where the line passes through (0.5,1.5).
To learn more about graph visit:https://brainly.com/question/17267403
#SPJ1
HELPP ILL GIVE BRAINLIEST

Answers
2-8 is -6 so we have 5^-6
We can rewrite exponents with a negative sign over 1 so we get
1/5^6 (A)
A vector v has initial point (-3,-2) and terminal point (-6,1). Write v in component form
Answers
Answer:
Step-by-step explanation:
Caleb started with 50 bacteria for his science experiment and they doubled in one day. Jenna also started with 50 bacteria for her experiment and after one day, her number of bacteria was equal to 50 to the second power. Choose the statement that is true for the number of bacteria after one day.