At which point on the curve y = √x is the tangent line parallel to the secant line joining two point on the curve whose x-coordinates are 1 and 4? a. (9/4. 3/2)
b. (0,0) c. (1/2, 1/√2)
d. (4,2) e None
Answers
To find the point on the curve y = √x where the tangent line is parallel to the secant line joining two points on the curve whose x-coordinates are 1 and 4, we first need to find the slope of the secant line.
Let's call the two points on the curve (1, √1) and (4, √4). The slope of the secant line is:
(√4 - √1)/(4 - 1) = 1/3
Next, we need to find the derivative of the function y = √x to find the slope of the tangent line at any point on the curve:
y' = (1/2)x^(-1/2)
Now we can set the slope of the tangent line equal to 1/3 and solve for x to find the point on the curve where the tangent line is parallel to the secant line:
(1/2)x^(-1/2) = 1/3
x^(-1/2) = 2/3
x = (9/4)
Plugging x = (9/4) into the original equation y = √x gives us the point on the curve:
y = √(9/4) = (3/2)
So the answer is (9/4, 3/2), or choice (a).
To determine at which point on the curve y = √x the tangent line is parallel to the secant line joining two points on the curve with x-coordinates 1 and 4, we'll need to find the slope of the secant line and then the slope of the tangent line.
First, find the two points on the curve:
P1: (1, √1) = (1,1)
P2: (4, √4) = (4,2)
Next, find the slope of the secant line using the formula (y2 - y1) / (x2 - x1):
m_secant = (2 - 1) / (4 - 1) = 1/3
Now, we'll find the derivative of y with respect to x to determine the slope of the tangent line:
y = √x = x^(1/2)
dy/dx = (1/2) * x^(-1/2)
To find the point where the slope of the tangent line equals the slope of the secant line (1/3), set dy/dx equal to 1/3 and solve for x:
(1/2) * x^(-1/2) = 1/3
x^(-1/2) = 2/3
x^(1/2) = 3/2
Square both sides:
x = (3/2)^2 = 9/4
Now, find the corresponding y-coordinate by plugging x back into the original equation:
y = √(9/4) = 3/2
Thus, the point at which the tangent line is parallel to the secant line is (9/4, 3/2), which corresponds to answer choice A.
To learn more about tangent line visit;
brainly.com/question/31326507
#SPJ11
Related Questions
suer easy answer orth alot of pions for you
10x-3=-5x-18
Answers
(10x-3=15x-18)
X = -1
Hey there!
\(Answer:\boxed{x=-1}\)
\(Explanation:\)
10x - 3 = -5x - 18
10x - 3 + 5x = -5x - 18 + 5x Add 5x to both sides
15 - 3 = -18
15x - 3 + 3 = -18 + 3 Add 3 to both sides
15x = -15
15x/15 = -15/15
x = -1
Hope this helps!
A cone 4.5 centimeters high with a radius of 3 centimeters. Label B is pointing to the circular base of the cone.
Answers
The volume of the cone isV = 42.41\(Cm^{3}\).
In order to calculate the volume of the solid, you use the following formula:
where
r: radius of the circular base of the cone = 3 cm
h: height from the circular base to the peak of the cone = 4.5 cm
You replace the values of r and h in the formula for the
volume V = \(\frac{1}{3}\) \(\pi\) \((3cm)^{2}\)4.5 =42.411 \(cm^{3}\) = 42.41 \(cm^{3}\)
Hence, the volume of the cone is 42.41 \(Cm^{3}\)
Volume may be a measure of occupied three-dimensional space. it's often quantified numerically using SI derived units (such as the cubic meter and liter) or by various imperial units (such as the gallon, quart, cubic inch). The definition of length (cubed) is interrelated with volume. the quantity of a container is generally understood to be the capacity of the container; i.e., the quantity of fluid (gas or liquid) that the container could hold, instead of the amount of space the container itself displaces.In past , volume is measured using similar-shaped natural containers and afterward , standardized containers. Some simple three-dimensional shapes can have its volume easily calculated using arithmetic formulas. Volumes of more complicated shapes are often calculated with integral calculus if a formula exists for the shape's boundary.
To learn more about volume from the given link:
brainly.com/question/12649605
#SPJ9
x^2-2x+3k=0 find k with D>0
sorry for the bad example.
Answers
Step-by-step explanation:
b²-4ac>0
(-2)²-4(1×3k)>0
4-12k>0
-12k>-4
k<⅓
Answer:
Step-by-step explanation:
b²-4ac>0
(-2)²-4(1×3k)>0
4-12k>0
-12k>-4
k<⅓
rewrite the equation 4x 4y 20 in slope intercept form
Answers
The equation 4x + 4y = 20 can be rewritten in slope-intercept form as y = -x + 5.
The equation 4x + 4y = 20 can be rewritten in slope-intercept form, which is y = mx + b, where m represents the slope and b represents the y-intercept.
To rewrite the equation in slope-intercept form, we need to isolate y on one side of the equation.
Step 1: Subtract 4x from both sides of the equation:
4x + 4y - 4x = 20 - 4x
This simplifies to:
4y = -4x + 20
Step 2: Divide both sides of the equation by 4 to solve for y:
4y/4 = (-4x + 20)/4
This simplifies to:
y = -x + 5
Now, the equation is in slope-intercept form, y = -x + 5. In this form, we can easily identify the slope, which is -1, and the y-intercept, which is 5.
The slope (-1) indicates that for every increase of 1 unit in the x-direction, the y-value decreases by 1 unit. The y-intercept (5) represents the point where the line intersects the y-axis when x is 0.
So, the equation 4x + 4y = 20 can be rewritten in slope-intercept form as y = -x + 5.
Know more about slope-intercept here:
https://brainly.com/question/30216543
#SPJ11
find the convolution of f(t)=e−(5t) and g(t)={2,0,0≤t<4t≥4
Answers
The convolution of f(t) = e^(-5t) and g(t) = {2, 0, 0 ≤ t < 4; 0, t ≥ 4} is given by h(t) = {2e^(-5t), 0 ≤ t < 4; 2e^(-5(t-4)), t ≥ 4}.
The convolution of two functions f(t) and g(t) is defined as:
h(t) = ∫_0^t f(τ) g(t-τ) dτ
In this case, we have:
f(t) = e^(-5t)
g(t) = {2, 0, 0 ≤ t < 4; 0, t ≥ 4}
To find the convolution h(t), we need to split g(t) into two parts based on the value of t:
For 0 ≤ t < 4, we have g(t) = 2.
For t ≥ 4, we have g(t) = 0.
Therefore, we can write:
h(t) = ∫_0^t e^(-5τ) 2 dτ + ∫_4^t e^(-5τ) 0 dτ
Simplifying the second integral, we get:
h(t) = 2 ∫_0^t e^(-5τ) dτ
h(t) = 2 [-1/5 e^(-5τ)]_0^t
h(t) = 2 (-1/5 e^(-5t) + 1/5)
h(t) = 2e^(-5t) - 2/5, for 0 ≤ t < 4
For t ≥ 4, we have:
h(t) = ∫_0^4 e^(-5τ) g(t-τ) dτ + ∫_4^t e^(-5τ) g(t-τ) dτ
Since g(t-τ) is zero for t-τ < 0, we can simplify the first integral to:
∫_0^(t-4) e^(-5τ) 2 dτ
Using the same technique as before, we can evaluate this integral to get:
[-1/5 e^(-5τ)]_0^(t-4)
= -1/5 e^(-5(t-4)) + 1/5
For the second integral, we have g(t-τ) = 0, so it simplifies to 0.
Therefore, we have:
h(t) = -1/5 e^(-5(t-4)) + 1/5, for t ≥ 4
Combining the two expressions for h(t), we get:
h(t) = {2e^(-5t), 0 ≤ t < 4; 2e^(-5(t-4)), t ≥ 4}
Thus, the convolution of f(t) = e^(-5t) and g(t) = {2, 0, 0 ≤ t < 4; 0, t ≥ 4} is given by h(t) = {2e^(-5t), 0 ≤ t < 4; 2e^(-5(t-4)), t ≥ 4}.
To learn more about convolution click here : brainly.com/question/31481291
#SPJ11
The convolution of f(t) = e^(-5t) and g(t) = {2, 0, 0 ≤ t < 4; 0, t ≥ 4} is given by h(t) = {2e^(-5t), 0 ≤ t < 4; 2e^(-5(t-4)), t ≥ 4}.
The convolution of two functions f(t) and g(t) is defined as:
h(t) = ∫_0^t f(τ) g(t-τ) dτ
In this case, we have:
f(t) = e^(-5t)
g(t) = {2, 0, 0 ≤ t < 4; 0, t ≥ 4}
To find the convolution h(t), we need to split g(t) into two parts based on the value of t:
For 0 ≤ t < 4, we have g(t) = 2.
For t ≥ 4, we have g(t) = 0.
Therefore, we can write:
h(t) = ∫_0^t e^(-5τ) 2 dτ + ∫_4^t e^(-5τ) 0 dτ
Simplifying the second integral, we get:
h(t) = 2 ∫_0^t e^(-5τ) dτ
h(t) = 2 [-1/5 e^(-5τ)]_0^t
h(t) = 2 (-1/5 e^(-5t) + 1/5)
h(t) = 2e^(-5t) - 2/5, for 0 ≤ t < 4
For t ≥ 4, we have:
h(t) = ∫_0^4 e^(-5τ) g(t-τ) dτ + ∫_4^t e^(-5τ) g(t-τ) dτ
Since g(t-τ) is zero for t-τ < 0, we can simplify the first integral to:
∫_0^(t-4) e^(-5τ) 2 dτ
Using the same technique as before, we can evaluate this integral to get:
[-1/5 e^(-5τ)]_0^(t-4)
= -1/5 e^(-5(t-4)) + 1/5
For the second integral, we have g(t-τ) = 0, so it simplifies to 0.
Therefore, we have:
h(t) = -1/5 e^(-5(t-4)) + 1/5, for t ≥ 4
Combining the two expressions for h(t), we get:
h(t) = {2e^(-5t), 0 ≤ t < 4; 2e^(-5(t-4)), t ≥ 4}
Thus, the convolution of f(t) = e^(-5t) and g(t) = {2, 0, 0 ≤ t < 4; 0, t ≥ 4} is given by h(t) = {2e^(-5t), 0 ≤ t < 4; 2e^(-5(t-4)), t ≥ 4}.
To learn more about convolution click here : brainly.com/question/31481291
#SPJ11
what is the sum of the interior angles of an equilateral triangle?
Answers
Answer:
180°is the sum of the interior angles of an equilateral triangle
The area of the green square is 9ft. The area of the yellow square is 25 ft.
What is the area of the red square (labelled "b" in the diagram)?
A)5 ft²
B)16 ft2
C)81 ft2
D)128 ft2

Answers
Answer:
B
Step-by-step explanation:
a²+b²=c²
3²+b²=5²
b²=5²-3²
b²=25-9=16 answer is 16
Juan says that for
every 1 soda, there
are 2 donuts?
Answers
Answer:
we need the rest of the question
Answer:
what is the question
Step-by-step explanation:
And what are the answer choices
can someone help please

Answers
Answer:
1.6
Step-by-step explanation:
Which set of ordered pairs represents a function?
{(7,-3), (9,-9), (7,9), (5, 1)}
o {(2,8),(-1, -7), (-2,-3), (-8,–7)}
{(-2,7), (6,6), (9,-6), (6, -7)}
{(5,7),(-9,-4), (0, -5), (0, -2)}
Answers
Answer:
(2,8), (-1,-7), (-2,-3), (-8,-7)
Step-by-step explanation:
It's this one because each input (x axis) has one and only one output (y axis) The others the input has more than one output making them wrong. Hope this helps
Use long division to solve:
69 )310.5
Answers
69)310.5
69)621/2
69*2/621
=2/9
Which expression will help find the volume of the figure?

Answers
Answer:
D. 1x9x4
Step-by-step explanation:
V= l x w x h
there are 10 balls in a bag: 4 blue, 3 red, 2 green, and 1 yellow. you pull balls from the bag one at a time and line them up on the table [in the order that you pulled them out]. how many different arrangements of balls could you end up with? select all that apply. group of answer choices
Answers
There are 3,628,800 different arrangements of balls that could be pulled out of the bag. None of the answer choices given are correct, as they all suggest a number smaller than the actual number of arrangements
To calculate the number of different arrangements of balls that can be
pulled out of the bag, we need to use the formula for permutations.
Since there are 10 balls in the bag, we have 10 choices for the first ball, 9
choices for the second ball, 8 choices for the third ball, and so on.
Therefore, the total number of arrangements is:
10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 3,628,800
So, there are 3,628,800 different arrangements of balls that could be
pulled out of the bag.
None of the answer choices given are correct, as they all suggest a
number smaller than the actual number of arrangements.
for such more question on arrangements
https://brainly.com/question/22008756
#SPJ11
Eli, Freda and Geoff were given 800 pounds to share in the ratio of there age. Eli is 9 years old Freda is 13 years old and Geoff is 18 years old. How much should they each have?
Answers
a. To find 40% of 75, Priya calculates. Does her calculation give the correct
value for 40% of 75? Explain or show how you know.
b. If represents a number, does always represent 40% of that number?
Explain your reasoning.
Answers
40 percentage of 75 is 30 and 2/5 of 75 is 30. So, Priya calculated in a correct way.
Given,
To find 40% of 75, Priya calculates 2/5 of 75
We have to find the value of 40% of 75.
Percentage;
A value or ratio that may be stated as a fraction of 100 is referred to as a percentage in mathematics. If we need to calculate a percentage of a number, we should divide it by its entirety and then multiply it by 100. The proportion therefore refers to a component per hundred. Per 100 is what the word percent means. The sign "%" is used to denote it.
Now,
Lets find;
40% of 75
40/100 × 75 = 40/4 × 3 = 10 × 3 = 30
That is,
40% of 75 is 30.
Now,
2/5 of 75
2/5 × 75 = 2 × 15 = 30
That is,
2/5 of 75 is also 30
Therefore,
40 percentage of 75 is 30 and 2/5 of 75 is 30. So, Priya calculated in a correct way
Learn more about percentage here;
https://brainly.com/question/11886240
#SPJ1
An artist is going to cut four similar right triangles from a rectangular piece of paper like the one shown to the right. What is BE to the nearest tenth when AC=13

Answers
The measurement of altitude BE is 4 unit.
What is an altitude?As the average level of the sea's surface, sea level is used to measure altitude. A high altitude is defined as being significantly higher than sea level, such as Mount Everest. It is referred to as having a low altitude when something is closer to the ground, like a plane coming in to land.
As ABCD is rectangle
AD = BC = 12
ΔABC = ΔBCD
BE = FD
5² = 3²+BE²
AE = 3
BE = √(5²-3²)
BE = 4
Thus, The measurement of altitude BE is 4 unit.
To learn mote about altitude refer to :
https://brainly.com/question/18530806
#SPJ1
Let P(t) represent the amount of a certain drug, in milligrams, that is in the bloodstream at time t hours. The rate at which the drug leaves the bloodstream is proportional to the amount of the drug in the bloodstream. The amount of the drug in the bloodstream can be modeled by dP/dt = kP, where k is a constant and t is time, in hours. At time t = 0,500 milligrams of the drug was administered. At the moment when the amount of the drug in the bloodstream is 50 milligrams, the amount is decreasing at a rate of 11.5 milligrams per hour. Which of the following is an expression for P (t)?
A. P(t) = 500 – 0.23t.
B. P(t) = 500 – 0,23 42.
C. P(t) = 500e -0.231.
D. P(t) = e-0.23+ + 499.
Answers
As proportional relationship, the amount decreasing at a rate milligrams per hour can be written in expression P(t) = 500 + e⁻⁰²ˣ
What is Proportional relationship?In math, the relationships between two variables where their ratios are equivalent is known as proportional relationship.
Given that P(t) represent the amount of a certain drug, in milligrams, that is in the bloodstream at time t hours.
Here we have the rate at which the drug leaves the bloodstream proportional to the amount of the drug bloodstream.
The amount of the drug in the bloodstream can be modeled by dP/dt = kP, where k is a constant and t is time, in hours.
Here we need to find the expression.
Bloodstream = 500 milligrams
So, the expression for this proportional relationship is written as;
P(t) = 500 + e⁻⁰²ˣ
To know more about Proportional relationship here.
brainly.com/question/29765554
#SPJ2
Write the number in 2 equivalent forms as a fraction, decimal, or percent.0.40
Answers
Answer:
2/5 or 40%
Step-by-step explanation:
.40 is 40 hundredths or 40/100
40/100 can be reduced to 20/50 and reduced again to 10/25 and one more time to 2/5
Percentages are fractions out of 100 so 40/100 would be 40%.
7. Find the coordinates of a point on a circle with radius 20 corresponding to an angle of \( 305^{\circ} \)
Answers
Given that a circle with radius 20 has a corresponding angle of 305°.
To find the coordinates of a point on the circle, we use the formula:`(r cos (θ), r sin (θ))`Here, `r = 20` and `θ = 305°`.
Substituting the values of `r` and `θ` in the formula, we get:`(20 cos (305°), 20 sin (305°))`
Using the values of trigonometric ratios, we can write:cos(305°) = cos(360° - 305°) = cos(55°) ≈ -0.5736sin(305°) = sin(360° - 305°) = sin(55°) ≈ 0.8192
Hence, the coordinates of a point on a circle with radius 20 corresponding to an angle of 305° are approximately `(-11.47, 16.38)`.
The coordinates of a point on a circle with radius 20 corresponding to an angle of 305° are approximately `(-11.47, 16.38)`
To know more about coordinates visit:
https://brainly.com/question/32836021
#SPJ11
A plane is flying at 25

Answers
The angle of depression the plane should descend is 1.43 degrees.
How to find the angle of depression?A plane is flying at an altitude of 25,000 ft when it start it descent to the airport. The plane is a horizontal distance of 1000,000 ft from the airport.
Therefore, let's find the angle of depression.
Hence, this situation forms a right angle triangle.
Therefore,
tan ∅ = opposite / adjacent
where
∅ = angle of depressionHence,
tan ∅ = 25000 / 1000000
∅ = tan⁻¹ 25 / 1000
∅ = tan⁻¹ 0.025
∅ = 1.43209618416
∅ = 1.43 degrees
learn more on right triangle here: https://brainly.com/question/3770177
#SPJ1
Congruent angle pairs : find value of x and the value of y

Answers
pls help asap if you can!!

Answers
The ∆ABC is an isosceles triangle and have the base angles m∠A and m∠C equal to 51° and the angle m∠B is equal to 78°.
What is an Isosceles triangleAn isosceles triangle have the measure of its base angles to be equal, and the sum of the interior angles sum up to 180°.
Given that sides AB ≅ BC, then the triangle ∆ABC has two sides with similar length and base angles so;
angles m∠A and m∠C are the base angles are both equal to 51°
m∠B = 180° - (51 + 51)° {sum of interior angles of a triangle}
m∠B = 180° - 102°
m∠B = 78°
Therefore, the isosceles triangle ∆ABC have the base angles m∠A and m∠C equal to 51° and the angle m∠B is equal to 78°.
Read more about Isosceles triangle here:https://brainly.com/question/1475130
#SPJ1
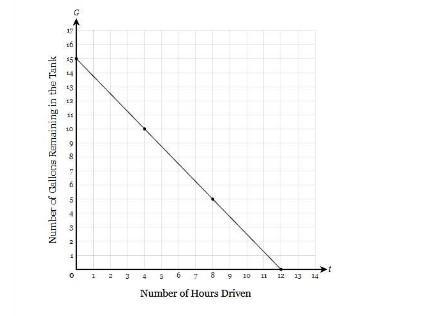
Serenity filled up her car with gas before embarking on a road trip across the country. Let � G represent the number of gallons of gas remaining in her gas tank after driving for � t hours. A graph of � G is shown below. Write an equation for � G then state the � y-intercept of the graph and determine its interpretation in the context of the problem.
Answers
The equation is: G = -⁵/₄t + 15
The slope of the function represents that ⁵/₄ gallons of gas is consumed to drive the car for one hour.
How to find the linear equation of the graph?The formula for the equation of a line in slope intercept form is:
y = mx + c
where:
m is slope
c is y-intercept
From the graph, we see that:
y-intercept = 15 gallons
Now, the slope is gotten from the formula:
Slope = (y₂ - y₁)/(x₂ - x₁)
Slope = (10 - 5)/(4 - 8)
Slope = -⁵/₄
Thus, equation is:
G = -⁵/₄t + 15
The slope of the function represents that ⁵/₄ gallons of gas is consumed to drive the car for one hour.
Read more about Linear equation graph at: https://brainly.com/question/28732353
#SPJ1
A city's population has increased 40% in the last 5 years and is now 53,782 people.
What was the population 5 years ago?
Answers
Given:
A city's population has increased 40% in the last 5 years and is now 53,782 people.
To find:
The population 5 years ago.
Solution:
Let x be the population 5 years ago.
A city's population has increased 40% in the last 5 years.
So, present population is
\(x+x\times \dfrac{40}{100}=x+0.4x=1.4x\)
It is given that the present population is 53782.
\(1.4x=53782\)
\(x=\dfrac{53782}{1.4}\)
\(x=38415.7142857\)
\(x\approx 38416\)
Therefore, the population 5 years ago was about 38416.
Complete the square
x^2 - 2x - 14 = 0
Answers
To complete the square for the equation x^2 - 2x - 14 = 0, follow these steps:
1. Move the constant term to the right side of the equation: x^2 - 2x = 14
2. Take half of the coefficient of x, square it, and add it to both sides of the equation: x^2 - 2x + 1 = 15
3. Factor the left side of the equation as a perfect square: (x - 1)^2 = 15
4. Take the square root of both sides of the equation, remembering to include both the positive and negative square roots: x - 1 = ±√15
5. Add 1 to both sides of the equation to isolate x: x = 1 ± √15
Therefore, the solutions to the equation x^2 - 2x - 14 = 0 are x = 1 + √15 and x = 1 - √15.
The nth term of a sequence is given by 3n(squared) what is the position of the term in the sequence that is the first one with a greater value than 1000?
Answers
To determine the position of the term in the sequence that first has a value greater than 1000, we need to solve the inequality 3n^2 > 1000. The position of the term is approximately 19.
We are given that the nth term of the sequence is given by 3n^2. We need to find the position (value of n) at which the term exceeds 1000.
To solve this, we set up the inequality:
3n^2 > 1000
Dividing both sides by 3, we have:
n^2 > 333.33
Taking the square root of both sides, we get:
n > √333.33
Approximating the square root of 333.33 to the nearest whole number, we find:
n > 18.24
Since n represents the position of the term in the sequence, it must be a positive whole number. Therefore, the smallest value of n that satisfies the inequality is 19.
Hence, the position of the term in the sequence that first has a value greater than 1000 is approximately 19.
Learn more about inequality here:
https://brainly.com/question/20383699
#SPJ11
what step is needed when constructing a circle circumscribed about a triangle?
Answers
Draw the circle with the center at the intersection of the perpendicular bisectors and the radius equal to the distance found in step 4.
When constructing a circle circumscribed about a triangle, the following step is needed:
Identify the three vertices of the triangle.
Let's say the triangle has vertices A, B, and C.
Find the perpendicular bisectors of the triangle's sides.
For each side of the triangle, construct a line that is perpendicular to the side and passes through its midpoint.
Locate the point of intersection of the perpendicular bisectors.
The point where all three perpendicular bisectors intersect is the center of the circumscribed circle.
Measure the distance from the center to any of the triangle's vertices.
This distance is the radius of the circumscribed circle.
By following these steps, you can construct a circle that passes through all three vertices of the triangle. This circle is known as the circumscribed circle or circumcircle of the triangle. It is unique to each triangle and provides a useful geometric property that can be applied in various mathematical and geometric contexts.
Learn more about circle at: brainly.com/question/12930236
#SPJ11
1/4 subtract by 1 1/2
Answers
Answer:
Step-by-step explanation:
1.5 - 0.25 = 1.25 = 1 1/4
We can turn both fractions into decimals.
1/4 = 0.25
1 1/2 = 1.5
Subtract.
0.25 - 1.5 = -1.25
Turn back into a fraction.
-1.25 = -1 1/4
Best of Luck!
Solve the initial-value problem of the 2nd order homogeneous differential equation I y" + 16 y = 0, y(0) = y'(0) = -2.
Answers
The particular solution of the given differential equation is : y(x) = -2cos(4x) - (1/2)sin(4x).
Given the differential equation is: I y" + 16 y =0 with initial values y(0) = -2, and y'(0) = -2.
We have to find the solution of the differential equation. We know that the standard form of a second-order homogeneous differential equation is:
y"+p(x)y'+q(x)y=0
The characteristic equation is obtained by substituting y=e^(mx) in the above equation. The characteristic equation is:
m²+p(x)m+q(x)=0
Comparing the above equation with
y" + 16 y = 0, we have,
p(x) = 0 and q(x) = 16
Therefore, the characteristic equation becomes:
m² + 16 = 0
m = ±4i
Hence, the general solution of the given differential equation is:
y(x) = c1cos(4x) + c2sin(4x). Now, let us apply the initial conditions:
y(0) = c1 = -2
Also, y'(x) = -4c1sin(4x) + 4c2cos(4x)Therefore,
y'(0) = 4= c2 = -2
c2 = -1/2
Therefore, the particular solution of the given differential equation is y(x) = -2cos(4x) - (1/2)sin(4x).
To know more about the differential equation, visit:
brainly.com/question/32524608
#SPJ11
Question 3 Let X1, X2,..., Xn be independent random variables, each having a uniform distri- bution over (0,1). Let M = maximum (X₁, X₂,..., Xn). Show that the distribution function of M, FM(-), is given by FM(x)=x, 0≤x≤1 What is the probability density function of M?
Answers
The distribution function of M, FM(-), is given by FM(x) = x, 0 ≤ x ≤ 1.
The probability density function of M is\(fM(x) = n * x^(^n^-^1^)\), 0 ≤ x ≤ 1.
In order to understand the distribution function of M, we need to consider the probability that M is less than or equal to a given value x. Since each Xi is uniformly distributed over (0,1), the probability that Xi is less than or equal to x is x.
For M to be less than or equal to x, all of the random variables Xi must be less than or equal to x. Since these variables are independent, their joint probability is the product of their individual probabilities. Therefore, the probability that M is less than or equal to x can be expressed as the product of n x's: P(M ≤ x) = x * x * ... * x = \(x^n\).
The distribution function FM(x) is defined as the probability that M is less than or equal to x. Therefore, FM(x) = P(M ≤ x) = \(x^n\).
To find the probability density function (PDF) of M, we differentiate the distribution function FM(x) with respect to x. Taking the derivative of \(x^n\)with respect to x gives us \(n * x^(^n^-^1^)\). Since the range of M is (0,1), the PDF is defined only within this range.
The distribution function of M is FM(x) = x, 0 ≤ x ≤ 1, and the probability density function of M is \(fM(x) = n * x^(^n^-^1^)\), 0 ≤ x ≤ 1.
Learn more about probability
brainly.com/question/32575884
#SPJ11