Apply the distributive property to create an equivalent expression.
4(3+1/4c- 1/2d)=

Answers
Answer:
4(3+1/4c-1/2d)
12+c-2d
Let me know if this helps!
Related Questions
recall that the work done by f to move a particle along an oriented curve is the line integral of f along this curve
Answers
The given statement "the work done by f to move a particle along an oriented curve is the line integral of f along this curve" is true.
The work done by a force vector field F to move a particle along an oriented curve is given by the line integral of F along that curve. The line integral represents the sum of the dot products between the force vector field F and the tangent vectors to infinitesimal line segments along the curve.
Mathematically, the work done W is expressed as:
W = ∮ F · dr,
where ∮ represents the line integral, F is the force vector field, dr is the differential displacement vector along the curve, and the dot product (·) indicates vector multiplication.
The line integral takes into account both the magnitude and direction of the force field along the curve, allowing us to calculate the total work done by the force as the particle moves along the path.
For such more question on curve:
https://brainly.com/question/31012623
#SPJ8
The following qquestion may be like this:
recall that the work done by f to move a particle along an oriented curve is the line integral of f along this curve. True or False.
Hi can anyone work this out.
Evaluate
25 1/2
Answers
Answer:
25.5
Step-by-step explanation:
In(e^3 x^4), where x>0
Answers
Answer:In(e^3 x^4) simplifies to 3x^4.
Step-by-step explanation:
In(e^3 x^4) simplifies to just 3x^4, since the natural logarithm (ln or In) and exponential function (e^x) are inverse functions of each other.
To see why, recall that ln(e^y) = y for any real number y, and e^(ln x) = x for any positive real number x. Therefore:
ln(e^3 x^4) = 3x^4 ln(e) (using the rule ln(xy) = ln(x) + ln(y) and ln(e) = 1)
= 3x^4 * 1 (since ln(e) = 1)
= 3x^4
A recent survey compared the mean end-of-the-month balance of credit card holders who applied for the car on their own and those who were contacted by telemarketers. For a sample of 12 self-applied card holders, its mean balance is $1,600 with a standard deviation of $350; for a sample of 10 contacted card holders, its balance is $1,950 with a standard deviation of $850. It is assumed that the two populations do not have equal standard deviations. Use the .01 significance level, is it reasonable to conclude that the mean balance is larger for the card holders who were contacted by telemarketers? Question to address here: what is the value of the test statistic? Select one: a. z=1.24 b. t=1.219 c. z=1.22 d. t=32.757 e. t=1.215
Answers
Based on the given data, the answer is that the value of the test statistic is t = 1.219.
To explain further, to compare the mean balances of the two groups (self-applied card holders and contacted card holders), we can conduct a two-sample t-test. This test helps us determine if there is a significant difference between the means of the two populations.
Given the information provided, we have the sample mean and standard deviation for each group. For the self-applied card holders, the sample mean is $1,600 with a standard deviation of $350, based on a sample size of 12. For the contacted card holders, the sample mean is $1,950 with a standard deviation of $850, based on a sample size of 10.
To calculate the test statistic, we use the formula:
\[t = \frac{{\bar{X_1} - \bar{X_2}}}{{\sqrt{\frac{{s_1^2}}{{n_1}} + \frac{{s_2^2}}{{n_2}}}}}\]
where \(\bar{X_1}\) and \(\bar{X_2}\) are the sample means, \(s_1\) and \(s_2\) are the sample standard deviations, and \(n_1\) and \(n_2\) are the sample sizes.
Plugging in the values, we get:
\[t = \frac{{1600 - 1950}}{{\sqrt{\frac{{350^2}}{{12}} + \frac{{850^2}}{{10}}}}}\]
\[t = 1.219\]
Therefore, the value of the test statistic is t = 1.219.
Learn more about test statistic here:
brainly.com/question/31746962
#SPJ11
x - 2/5 = 1/6
what is the answer for x?
Answers
Answer:
17/30
Step-by-step explanation:
Answer:
x=17/30
Step-by-step explanation:
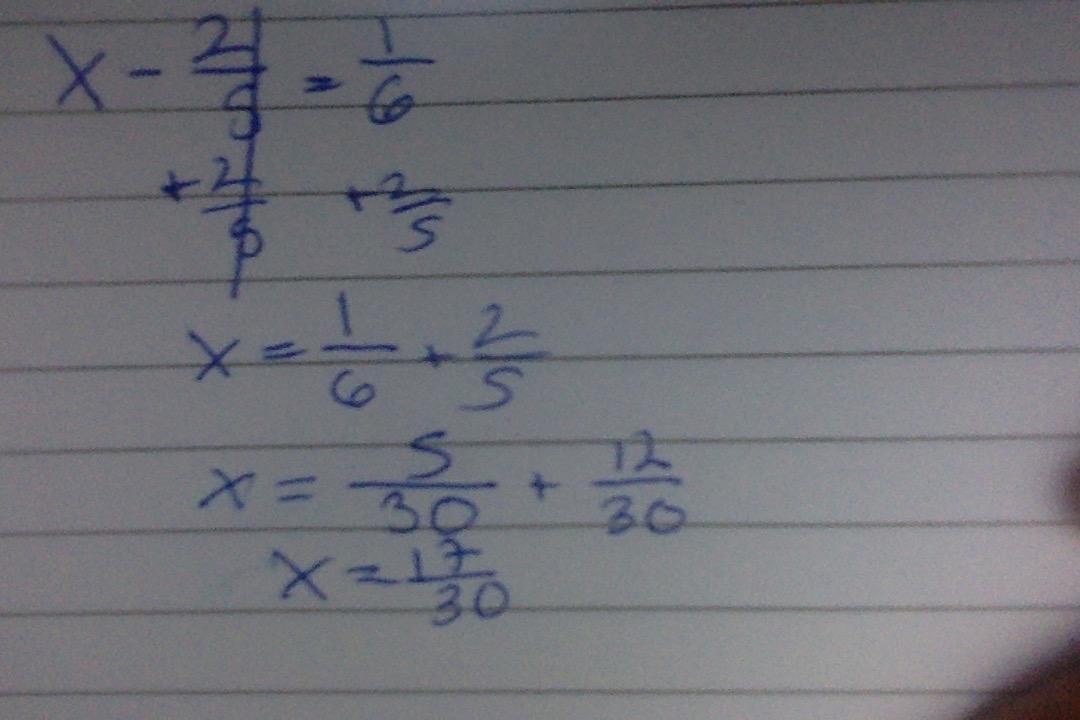
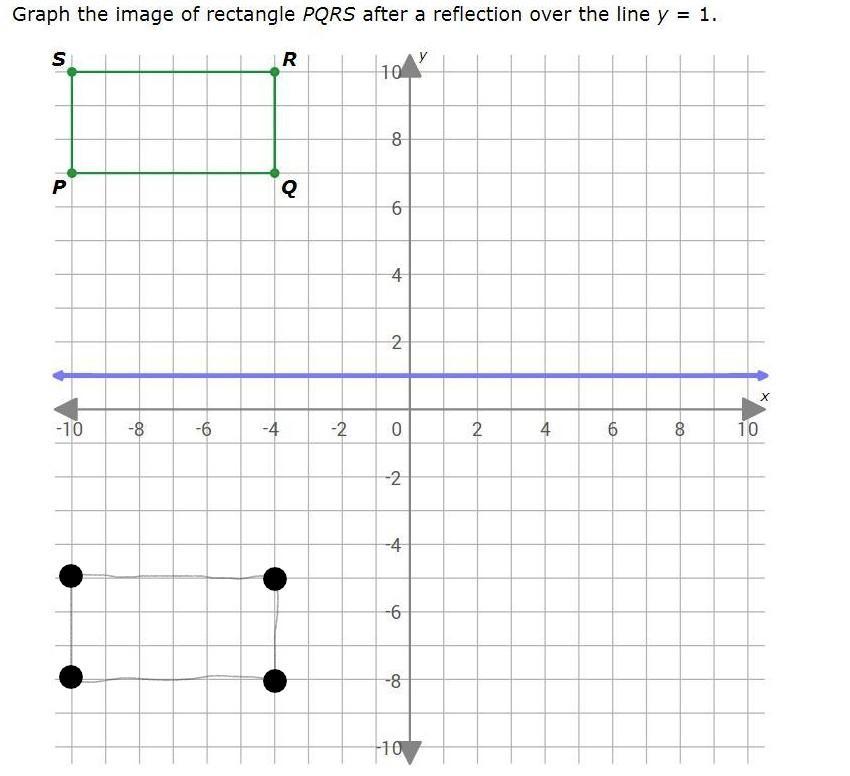
reflect..............................................

Answers
Answer:
Q (-4,-5)
R (-4,-8)
P (-10,-5)
S (-10,-8)
Step-by-step explanation:
A tree is 55 meters tall. What is its height in feet? Use the following conversion: 1 meter is 3.3 feet.
Answers
So you're telling me, you're seriously in high school and do not know this.
Ah, whatever.
Tree height = 55 meters
Tree height in feet = ?
1 m = 3.3 feet
Tree height in feet = 55 x 3.3 = 181.5 feet.
The required answer is the height of the tree is provided in meters (55 meters) in the given problem and convert it to 181.5 feet. By multiplying the given height by the conversion factor of 3.3 feet/meter, we obtain the height of the tree in feet
Feet to meter conversion:
To convert a value from feet to meters, we use the conversion factor of 1 meter equals 3.3 feet. This means that for every 1 meter, there are 3.3 feet. To convert a measurement from feet to meters, we multiply the given value in feet by the conversion factor.
To convert the height of a tree from meters to feet, we can use the conversion factor: 1 meter is equal to 3.3 feet. Let's solve the problem step by step:
Step 1: Multiply the given height in meters (55) by the conversion factor (3.3).
55 meters x 3.3 feet/meter
Step 2: Perform the multiplication operation:
55 x 3.3 = 181.5 feet
Step 3: Write the result as the height in feet:
The height of the tree is 181.5 feet.
Hence, the height of the tree is provided in meters (55 meters) in the given problem , and to convert it to 181.5 feet. By multiplying the given height by the conversion factor of 3.3 feet/meter, we obtain the height of the tree in feet.
Learn more about unit conversions and the relationship between feet and meters at:
https://brainly.com/question/16814684
#SPJ6
15. I had 180 mL of water in a measuring cylinder. I added a stone. The reading is now 195 mL. What is the volume of the stone?
Answers
Answer: 15 mL
Step-by-step explanation:
Before the stone the reading was 180 mL
When the stone was added the reading rose to 195 mL
So, we subtract them both, this will give us the volume of the stone
195 mL - 180 mL = 15 mL
180 mL of water in a measuring cylinder and then added a stone, The reading is now 195 mL, the volume of the stone is, 15 ml
What is Volume?In mathematics, Space occupied by three dimensional objects is called Volume. Basically it is a space within a closed region of every three dimensional object.
Given that,
water in a measuring cylinder = 180 ml
Then, a stone added
The reading = 195 mL
Now, increased volume = 195 - 180
= 15
Volume of stone = Increased volume
Therefore, Volume of stone is 15 ml
To know more about Volume check:
https://brainly.com/question/13338592
#SPJ2
find the 36th term of the arithmetic sequence 156,153,150
Answers
Answer: 51
Step-by-step explanation:
a = first term = 156
d = common difference = 153 - 156 = -3
The nth term will be gotten using the formula:
= a + (n - 1)d
36th term = a + (36 - 1)d = a + 35d
= 156 + 35(-3)
= 156 - 105
= 51
For each of the differential equations in Problems 9 through 11, find the first four nonzero terms in each of two power series solutions about the origin. Show that they form a fundamental set of solutions. What do you expect the radius of convergence to be for each solution? 9. y'' + (sin x)y = 0 10. e^xy'' + xy = 0 11. (cos x)y'' + xy'- 2y = 0
Answers
We will solve the differential equation and find the power series solutions for each problem.
Problem 9: y'' + (sin x)y = 0
Assuming the power series solution: y = a0 + a1x + a2x^2 + ...
Differentiating twice, we have:
y' = a1 + 2a2x + 3a3x^2 + ...
y'' = 2a2 + 6a3x + 12a4x^2 + ...
Substituting these expressions into the differential equation, we get:
2a2 + 6a3x + 12a4x^2 + ... + (sin x)(a0 + a1x + a2x^2 + ...) = 0
Grouping the terms by powers of x, we get:
a0(sin x) = 0
a1(sin x) + 2a2 = 0
a2(sin x) + 6a3 = 0
a3(sin x) + 12a4 = 0
...
From the first equation, we have a0 = 0, since sin(0) = 0. From the second equation, we have a2 = -a1(sin x)/2. From the third equation, we have a3 = -a2(sin x)/6 = a1(sin x)^2/12. From the fourth equation, we have a4 = -a3(sin x)/12 = -a1(sin x)^3/288.
Thus, we have the power series solution:
y = a1x - a1(sin x)^3/288 + ...
This solution is nontrivial, and the ratio of consecutive coefficients is:
-a1(sin x)^3/288 / (a1x) = -(sin x)^3 / (288x)
The ratio approaches zero as x approaches infinity, so the radius of convergence is infinite. Therefore, we expect the solution to be valid for all values of x.
Problem 10: e^xy'' + xy = 0
Assuming the power series solution: y = a0 + a1x + a2x^2 + ...
Differentiating twice, we have:
y' = a1 + 2a2x + 3a3x^2 + ...
y'' = 2a2 + 6a3x + 12a4x^2 + ...
Substituting these expressions into the differential equation, we get:
e^x(2a2 + 6a3x + 12a4x^2 + ...) + x(a0 + a1x + a2x^2 + ...) = 0
Grouping the terms by powers of x, we get:
a0 + (a1 + a0)x + [(2a2 + a1)x^2 + (6a3 + 2a2)x^3 + (12a4 + 6a3)x^4 + ...] = 0
Since the coefficient of x^0 is nonzero, we must have a0 = 0. Then, the coefficient of x^1 gives:
a1 + a0 = 0
a1 = 0
This means that the power series solution is identically zero, which is trivial. Therefore, we cannot form a fundamental set of solutions using power series.
Problem 11: (cos x)y'' + xy' - 2y = 0
Assuming the power series solution: y = a0 + a1x + a2x^2 + ...
Differentiating twice, we have:
y' = a1 + 2a2x + 3a3x
To learn more about differential equations refer below:
https://brainly.com/question/31583235
#SPJ11
Halp me this question

Answers
Answer:
In 14,689, 14 is the thousands group, and 689 is the ones group.
answer all or leave it for somebody else
Decimal number system uses a base of 10 ; binary system a bases 2 , octal system a base of 8 ; and hexadecimal system a base of \( 16 . \) What is the hexadecimal number representing the decimal numbe
Answers
A decimal number system uses a base of 10, and it includes 10 numerals: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Binary system uses a base of 2 and has only two numerals: 0 and 1.
The octal system has a base of 8, and it includes eight numerals: 0, 1, 2, 3, 4, 5, 6, and 7.
Finally, the hexadecimal system has a base of 16, and it includes sixteen numerals: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, and F. Each hexadecimal digit corresponds to four binary digits (bits).To convert a decimal number to hexadecimal, we use the division-remainder method.
This method involves the division of the decimal number by 16 and writing the remainder as a hexadecimal digit. If the quotient is less than 16, it is written as a hexadecimal digit.
To know more about decimal visit:
https://brainly.com/question/33109985
#SPJ11
. sand is being dumped from a truck at a rate of 40 cubic feet per minute forming a cone with diameter twice the height. how fast is the height changing when the pile is 5 feet high?
Answers
A farmer intends to share 32 goats amongst his sons john, peter and thomas in the ratio 1 : 3 : 4 respectively what fraction of the goats will peter get?
Answers
The number of goats Peter will have is 12.
What are ratios and proportions?An ordered pair of numbers a and b, represented as a / b, is a ratio if b is not equal to 0. A proportion is an equation that sets two ratios at the same value.
Given that a farmer intends to share 32 goats amongst his sons john, peter, and Thomas in the ratio 1 : 3: 4 respectively.
The number of the fractions will be calculated by assuming the common ratio as x. Then write an expression as below:-
x + 3x + 4x = 32
8x = 32
x = 32 / 8
x = 4
Number of goats for Peter = 3x
Number of goats for Peter = 3 x 4 = 12
Therefore, the number of goats Peter will have is 12.
To know more about ratios and proportions follow
https://brainly.com/question/12024093
#SPJ1
find (a) the slope of the curve at the given point p, and (b) an equation of the tangent line at p. y= 1/x; p(5,1/5)
Answers
Answer:
(a) -1/25
(b) y = -1/25x +2/5
Step-by-step explanation:
You want the slope and tangent line equation for the curve y = 1/x at point P(5, 1/5).
(a) SlopeThe slope is the derivative of the function at the given point:
y = 1/x = x^(-1)
y' = (-1)x^(-1-1) = -1/x²
At x=5, the slope is ...
m = -1/5² = -1/25
(b) EquationThe equation of the tangent line is conveniently written using slope-intercept form:
y -k = m(x -h) . . . . . . . . equation for line with slope m at point (h, k)
y -1/5 = -1/25(x -5) . . . . equation for line with slope -1/25 at point (5, 1/5)
Rearranging, we have the slope-intercept form ...
y = -1/25x +2/5
<95141404393>

what is the solution to this equation?
\( \sqrt[5]{27(x - 2) = 3?} \)
Answers
Answer:
x = 11
Step-by-step explanation:
27x - 54 = 243
x = 11
When one increases the confidence level (1-α), say from 0.90 to 0.95, what happens to the width of the confidence interval? a. It stays the same b. It becomes wider c. It becomes narrower
Answers
Step-by-step explanation:
A higher confidence interval means less power which in turns means a smaller rejection religion.So our confidence interval would become wider.
if the sin of angle x is four fifths and the triangle was dilated to be two times as big as the original, what would be the value of the sin of x for
Answers
According to the given statement the value of sin x = 8/10
What is trigonometry?A mathematical field called trigonometry examines connections between triangles' sides and angles. Due to the fact that every straight-sided shape can be decomposed into a group of triangles, trigonometry can be found throughout all of geometry.
How is trigonometry applied in the real world?To roof a home, to make the roof slant (in the case of single-family bungalows), to determine the height of a roof in buildings, etc., use trigonometry. The naval and aviation industries use it. It's applied to cartography (creation of maps). Trigonometry is also used in satellite navigation systems.
According to the given information:sin x = 4/5
We know that:
Sin x = opposite/Hypotenuse.
So,
When the triangle is enlarged, the opposite side will increase to an angle of 8, and the hypotenuse will increase to an angle of 10.
= 4/5 we multiply by 2 with 4 and 5 we get:
= 8/10
4/5 will result from simplifying 8/10. Thus, nothing has changed.
So the value of sin x = 8/10.
To know more about trigonometry visit:
https://brainly.com/question/26719838
#SPJ4
Hard calculus question, please only answer if you are capable.

Answers
Step 1:
Given data
Cardboard size:
Length = L = 16
Breadth = W = 30
Step 2:
Let x in square is cut from 4 corners and bended into a box whose size is now
L = 16 - 2x
W = 30 - 2x
H = x
find the greastest common factor of 10,30,and 45.
Answers
10/5 = 2
30/5 = 6
45/5 = 9
===================================================
Explanation:
Find the prime factorization of each value. A factor tree may help.
10 = 2*5
30 = 2*3*5
45 = 3*3*5
We see that '5' is found in each of the factorizations. This is the only factor that shows up in all three values, and it only shows up one time. So that's why 5 is the GCF.
Simplify (10y - 5g)(3s + 6g) using foil method
Answers
The solution is on the paper.

in a control chart, the ucl and lcl represent plus or minus three standard deviations. true and false
Answers
The statement-
In a control chart, the UCL and LCL represent plus or minus three standard deviations is true
What is control chart?
Control chart is a graph used to measure the how a change occurs in a process over time. There are three lines in a control chart. A central line which denotes the average, a lower line which denotes the lower control limit and an upper line which denotes the upper control limit.
In a control chart, the UCL is the Upper Control Limit and LCL is the Lower Control Limit.
LCL and UCL are three standard deviation from the mean of the data set
If s is the standard deviation of the sample, -3s is the LCL and +3s is the UCL
So the statement,
In a control chart, the UCL and LCL represent plus or minus three standard deviations is true
To learn more about Control chart, refer to the link-
https://brainly.com/question/26478724
#SPJ4
A survey of 125 freshmen business students at a local university produced the results listed below. How many students took history and math, but not music? 30 took history; 32 took math; 33 took music; 14 took history but not math; 9 took math and music; 13 took history and music; 2 took all three
Answers
Answer:
Total Number of students taking Math and History and not music are 68.
Number of students who took both math and history at the same time is 6.
Step-by-step explanation:
History = 30
Math = 32
Music= 33
Math and Music= 9
History and Music= 13
History and Music and Math = 2
History but not math = 14
We have to find students taking history and math but not music.
Total number of students = 125
From the figure number of students taking Math and History and not music are
=30+6+32= 68
Number of students who took both math and history at the same time is 6.

Identify the recursive formula for the sequence -3, 9, -27, 81, ....

Answers
Answer:
A
Step-by-step explanation:
there is a common ratio between consecutive terms , that is
9 ÷ - 3 = - 27 ÷ 9 = 81 ÷ - 27 = - 3
this indicates the sequence is geometric.
the recursive formula allows a term in the sequence to be found by multiplying the previous term by the common ratio r , that is
f(n) = - 3f(n - 1) if n > 1 : f(1) = - 3
how tall is three feet
Answers
Answer: if you mean Inches, its 25.
Answer:
36 inches or 1 yard
Step-by-step explanation:
6.2. Batteries The dataset batteries includes three separate data collection activities testing energizer and ultracell batteries. [36] Quoting from the article, In the first test, batteries were loaded with a camera flash, using 1000 mA loaded for 10 s/min for one hour per day. The number of "pulses" to reach pre-defined voltage levels was recorded. Nine Energizer batteries were used to reach 1 volt and 9 Ultracell batteries were used to reach 1 volt. (a) Why is this independent (2-group) data? (b) What is the categorical grouping variable? What are its possible values?
Answers
The data is independent (2-group) because it involves two separate groups (Energizer and Ultracell batteries) that are tested and compared separately.
In this study, the categorical grouping variable is the battery brand or type. It divides the data into two distinct groups: Energizer and Ultracell batteries. Each battery brand is tested separately, and their performance is measured in terms of the number of pulses required to reach pre-defined voltage levels.
By categorizing the data based on the battery brand, researchers can compare the performance of Energizer and Ultracell batteries and analyze any differences or similarities between them.
This independent (2-group) data setup allows for a focused investigation of the two battery brands and facilitates the assessment of their respective performance in the given test scenario.
To know more about Ultracell visit -
brainly.com/question/32575166
#SPJ11
what is y-2=-3 (x-7) in standard form
A.y-2=--3x+21
B.y=-3x+23
C.3x+y-23=0
D.3x+y=23
Answers
9514 1404 393
Answer:
D. 3x +y = 23
Step-by-step explanation:
If you know what "standard form" is, then you recognize that only one offered answer choice is actually in standard form. That is the correct choice.
3x + y = 23
_____
Standard form for a linear equation is ...
ax +by = c
where a, b, c are mutually prime integers and a ≥ 0. If a = 0, then b > 0. (The leading coefficient is positive.)
the time between arrivals of taxis at a busy intersection is exponentially distributed with a mean of
Answers
The probability of waiting longer than one hour for a taxi is approximately 0.5488
Let X be the time between arrivals of taxis at the intersection. Then, X follows an exponential distribution with a mean of 10 minutes, i.e., E(X) = 10.
We want to find the probability of waiting longer than one hour (i.e., 60 minutes) for a taxi. Let Y be the waiting time for a taxi. Then, Y = kX, where k is a constant.
We can find k as follows
E(Y) = E(kX) = kE(X) = 10k
Since the mean waiting time is one hour (i.e., 60 minutes), we have
E(Y) = 60 minutes = 1 hour
Therefore, we get
10k = 1
k = 1/10
Now we can find the probability of waiting longer than one hour for a taxi as follows
P(Y > 60) = P(kX > 60) = P(X > 6) [since k = 1/10]
where the last step follows from the fact that X follows an exponential distribution with mean 10, so P(X > x) = e^(-x/10) for any x > 0.
Therefore, we get
P(Y > 60) = P(X > 6) = e^(-6/10) = e^(-0.6) ≈ 0.5488
Learn more about probability here
brainly.com/question/30579294
#SPJ4
The given question is incomplete, the complete question is:
The time between arrivals of taxis at a busy intersection is exponentially distributed with a mean of 10 minutes. (a) What is the probability that you wait longer than one hour for a taxi?
Solve each system by graphing. Check your answer. Y=x-22x+y=1
Answers
We have the equations :
\(\begin{gathered} y\text{ = x - 2} \\ 2x\text{ + y = 1} \end{gathered}\)To solve graphically, we should plot the graph of the equation on the same graph.
For y = x-2
We can obtain two points to plot the graph of y = x-2
At x= 0:
\(\begin{gathered} y\text{ = 0-2} \\ =\text{ -2} \end{gathered}\)At y= 0:
\(\begin{gathered} 0=\text{ x-2} \\ x\text{ = 2} \end{gathered}\)We have the points : (0,-2) and (2,0)
For 2x + y =1
At x = 0:
\(\begin{gathered} 0\text{ + y = 1} \\ y\text{ =1} \end{gathered}\)At y = 0:
\(\begin{gathered} 2x\text{ + 0 = 1} \\ x\text{ = }\frac{1}{2} \end{gathered}\)We have the points : (0, 1) and (1/2, 0)
Plotting these points gives the graph shown below:
From the graph, we have the point of intersection of the two lines as (1,-1)
Hence, the solution to the system of equation is (1, -1)

R = x²/y.
x = 3.8 × 105
y = 5.9 × 104
Work out the value of R.
Give your answer in standard form to an appropriate degree of accuracy.

Answers
The value of the expression R = x^2/y when y = 3.8 x 10^5 and x = 5.9 x 10^4 is 9.2 x 10^3
What are expressions?Expressions are mathematical statements that are represented by variables, coefficients and operators
How to evaluate the expression?The expression is given as
R = x^2/y
Where
y = 3.8 x 10^5
x = 5.9 x 10^4
Substitute y = 3.8 x 10^5 and x = 5.9 x 10^4 in the equation R = x^2/y
So, we have
R = (5.9 x 10^4)^2/3.8 x 10^5
Evaluate the exponent in the above equation
So, we have
R = 34.81 x 10^8/3.8 x 10^5
Evaluate the quotient in the above equation
So, we have
R = 9.16052631579 x 10^3
Approximate the above expression
So, we have
R = 9.2 x 10^3
Hence, the value of the expression R = x^2/y when y = 3.8 x 10^5 and x = 5.9 x 10^4 is 9.2 x 10^3
Read more about scientific notation at
brainly.com/question/27862246
#SPJ1