Although all of the following systems can be solved via the substitution method, substitution would be the best method for solving which system.
Group of answer choices

Answers
Using the substitution method, the system of equation that is easily solved is:
c. y = 2x + 3
2x + y = 5
How to Solve A System of Equations Using the Substitution Method?Using the substitution method to solve a system of equations is best when one of the equations have one isolated variable that we can simply plug its value into the second equation.
For example, given the system of equations:
y = 2x + 3 --> eqn. 1
2x + y = 5 --> eqn. 2
Substitute y = (2x + 3) into eqn. 2 and find x:
2x + y = 5 --> eqn. 2
2x + 2x + 3 = 5
4x + 3 = 5
4x = 5 - 3
4x = 2
x = 2/4
x = 1/2
Substitute x = 1/2 into eqn. 1 to find y
y = 2x + 3 --> eqn. 1
y = 2(1/2) + 3
y = 1 + 3
y = 4
From the above, we can see that the system of equations that is quite easy to solve using the substitution method is:
c. y = 2x + 3
2x + y = 5
The rest of the equations are quite different and not as straightforward as solving as this using the substitution method.
Learn more about system of equations on:
https://brainly.com/question/14323743
#SPJ1
Related Questions
Please solve this
∫ (log(1 + x ^ 2))/((x + 1) ^ 2) dx
Answers
The final result of the integral is:
∫ (log(1 + x²) / (x + 1)²) dx = log(x + 1) - 2 (log(x + 1) / x) - 2Li(x) + C,
where Li(x) is the logarithmic integral function and C is the constant of integration.
We have,
To solve the integral ∫ (log(1 + x²) / (x + 1)²) dx, we can use the method of substitution.
Let's substitute u = x + 1, which implies du = dx. Making this substitution, the integral becomes:
∫ (log(1 + (u-1)²) / u²) du.
Expanding the numerator, we have:
∫ (log(1 + u² - 2u + 1) / u²) du
= ∫ (log(u² - 2u + 2) / u²) du.
Now, let's split the logarithm using the properties of logarithms:
∫ (log(u² - 2u + 2) - log(u²)) / u² du
= ∫ (log(u² - 2u + 2) / u²) du - ∫ (log(u²) / u²) du.
We can simplify the second integral:
∫ (log(u²) / u²) du = ∫ (2 log(u) / u²) du.
Using the power rule for integration, we can integrate both terms:
∫ (log(u² - 2u + 2) / u²) du = log(u² - 2u + 2) / u - 2 ∫ (log(u) / u³) du.
Now, let's focus on the second integral:
∫ (log(u) / u³) du.
This integral does not have a simple closed-form solution in terms of elementary functions.
It can be expressed in terms of a special function called the logarithmic integral, denoted as Li(x).
Therefore,
The final result of the integral is:
∫ (log(1 + x²) / (x + 1)²) dx = log(x + 1) - 2 (log(x + 1) / x) - 2Li(x) + C,
where Li(x) is the logarithmic integral function and C is the constant of integration.
Learn more about integrations here:
https://brainly.com/question/30217024
#SPJ1
The two windows shown are similar. What is the height of the larger window?

Answers
Answer:
the answer is 5.44 feet
Step-by-step explanation:
Add me
Answer:
Step-by-step explanation:

The following are the annual incomes (in thousands of dollars) for 8 randomly chosen, U.S. adults employed full-time.
44, 44, 54, 54, 65, 39, 54, 44
Send data to calculator
(a) What is the mean of this data set? If your answer is not an
integer, round your answer to one decimal place.
(b) What is the median of this data set? If your answer is not
an integer, round your answer to one decimal place.
(c) How many modes does the data set have, and what are
their values? Indicate the number of modes by clicking in the
appropriate dircle, and then indicate the value(s) of the
mode(s), if applicable.
0
Zero modes
one mode:
Two modes:
Answers
Answer:
(a) To find the mean of the data set, sum up all the values and divide by the total number of values.
44 + 44 + 54 + 54 + 65 + 39 + 54 + 44 = 398
Mean = 398 / 8 = 49.75
Rounded to one decimal place, the mean of this data set is 49.8.
(b) To find the median of the data set, i need to arrange the values in ascending order first:
39, 44, 44, 44, 54, 54, 54, 65
The median is the middle value in the sorted data set. In this case, we have 8 values, so the median is the average of the two middle values:
(44 + 54) / 2 = 98 / 2 = 49
Rounded to one decimal place, the median of this data set is 49.0.
(c) To determine the modes of the data set, identify the values that appear most frequently.
In this case, the mode refers to the value(s) that occur(s) with the highest frequency.
From the data set, i see that the value 44 appears three times, while the value 54 also appears three times. Therefore, there are two modes: 44 and 54.
x + 2y=-6
y = 2z =2
-2x- 6y + 5z =26
Answers
To eliminate y from the first equation, we can multiply the entire equation by -2. This will give us:
-2x - 4y = -12
Now, if we add this equation to the second equation, the y terms will cancel out, leaving us with:
-2x - 4(2) + 5z = 26
-2x + 5z = 26
Now we have two equations in two variables, x and z. We can solve this system of equations by substituting the value of y from the second equation into the first equation. This gives us:
x + 2(2) = -6
x = -10
Substituting this value of x into the second equation, we get:
-2(-10) + 5z = 26
20 + 5z = 26
5z = 6
z = 1.2
Finally, we can substitute the values of x and z back into the second equation to find the value of y:
-2(-10) - 6(1.2) + 5(1.2) = 26
20 - 7.2 + 6 = 26
12.8 = 26
This system of equations has no solution, since we have found values of x and z that make the second equation true, but substituting these values into the first equation results in a false statement. This means that there is no set of values for x, y, and z that will make all three equations true at the same time.
A cup of brewed tea has 54 milligrams less caffeine than a cup of brewed coffee. If a cup of tea has 66 milligrams of caffeine, how much caffeine is in a cup of coffee?
Answers
Answer:
120 milligrams
Step-by-step explanation:
x=coffee
x-54=tea
x-54=66
x=66+54=120
Find the sum. 54.703 + 298.1
Answers
For the following paired data, (1) Calculate the correlation coefficient, r, and (2) at the 0.05 significance level, determine whether there exists a linear correlation.x | 2 4 5 6y | 6 9 8 10
Answers
Answer:
Linear correlation exists
Step-by-step explanation:
Given the data :
X : | 2 4 5 6
Y : | 6 9 8 10
Using technology to fit the data and obtain the correlation Coefficient of the regression model,
The Correlation Coefficient, r is 0.886
To test if there exists a linear correlation :
Test statistic :
T = r / √(1 - r²) / (n - 2)
n = number of observations
T = 0.886 / √(1 - 0.886²) / (4 - 2)
T = 0.866 / 0.3535845
T = 2.449
Comparing Pvalue with α
If Pvalue < α ; Reject H0
Pvalue = 0.1143
α = 0.05
Pvalue > α ; We reject the null and conclude that linear correlation exists
PLS HELP idk how to do this

Answers
Answer:
this figure regular hexagon have rotation symmetry. The order is 6 and the degrees is 120
A car purchased for $15,000 today will be worth 6% less each year. How much
will the car be worth at the end of 5 years? Write the exponential function to model the increase. Calculate the value of the car in 5 years
Answers
Answer:
$11,008.56.
Step-by-step explanation:
6% less each year means that the car is worth (100 - 6) = 94% or 0.94 of the previous year,
The function is:
f(t) = 15000(0.94)^t where t = the times in years.
After 5 years the value =
15000(0.94)^5
= $11008.56
Edith made a bag of trail mix with 1/2 cup of pecans, 3/5 cup of apple slices, and 2/7 cup of pumpkin seeds. About how much trail mix did Edith make?
PLS HELP
Answers
Edith made about 97/70 cups of trail mix. The solution has been obtained by using ratios.
What is a ratio?
A ratio is produced by comparing or compressing two related bits of data. By counting the reciprocity of the relationship, we can determine the frequency with which one quantity equals another. A ratio is a number that can be used to show how much one thing is in comparison to another, to put it simply.
We are given that Edith made a bag of trail mix with 1/2 cup of pecans, 3/5 cup of apple slices, and 2/7 cup of pumpkin seeds.
So, the total amount of trail mix is:
⇒1/2 cup of pecans + 3/5 cup of apple slices + 2/7 cup of pumpkin seeds
⇒1/2 + 3/5 + 2/7
⇒(35 + 42 + 20)/70
⇒97/70
Hence, Edith made about 97/70 cups of trail mix.
Learn more about ratio from the given link
https://brainly.com/question/12024093
#SPJ1
Use the general slicing method to find the volume of the following solid. The solid with a semicircular base of radius 11 whose cross sections perpendicular to the base and parallel to the diameter are squares
Answers
The volume of the solid is 1789.33
For a circle of radius 11, we have the following equation:
x²+y²=11²
x²+y²=121
Now, making it explicit for x:
\(x=\sqrt{121-y^2}\)
Then, if we consider that for a height y, the length x is double, we have that the length of each cross-section is given by:
\(s=\sqrt[2]{81-y^2}\)
With this, we can propose the following integral to obtain the volume that they are asking us:
\(\int\limits^1_0 {s^2} \ \, dy \\\int\limits^1_0 ({\sqrt[2]{121-y^2})^2 } \, dy\\\\\int\limits^1_0 {4*(121-y^2)} \, dy\\\\4*(121y-\frac{y^3}{3} )\)
Finally, calculating, we have that the volume is V=1789.33
To know more about the volume of solid:
https://brainly.com/question/20284914
#SPJ4
Enter the number that belongs in the green box
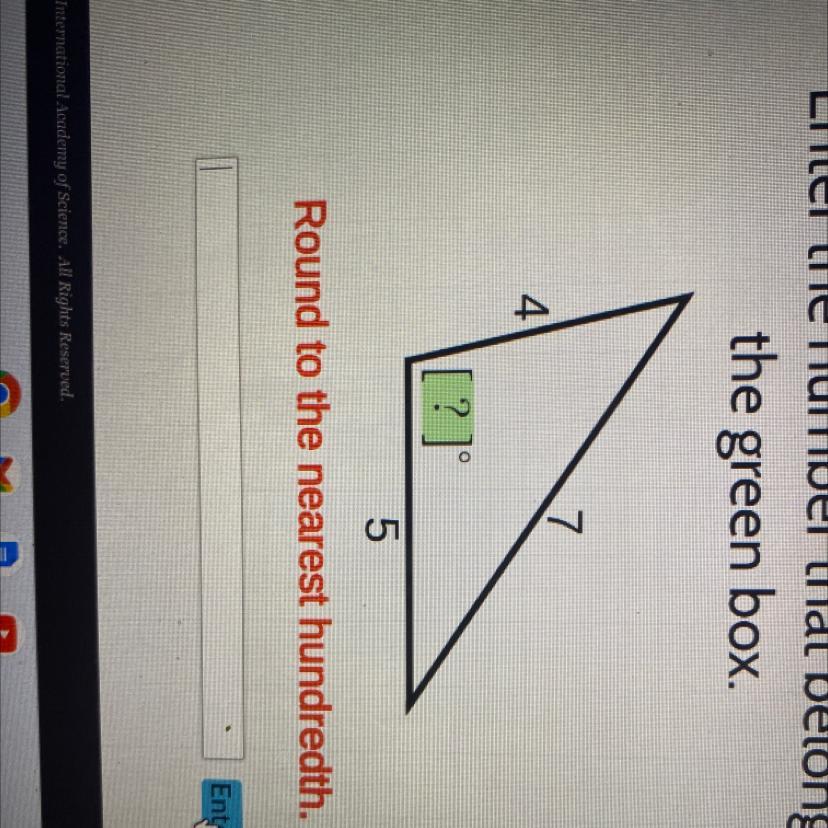
Answers
The angle between the sides measuring 4 and 5 in the obtuse triangle is approximately 101.54 degrees.
To find the measure of the angle between the sides measuring 4 and 5 in an obtuse triangle with side lengths 4, 5, and 7, we can use the Law of Cosines. The Law of Cosines states that in a triangle with side lengths a, b, and c, and an angle opposite to side c, the following equation holds:
\(c^2 = a^2 + b^2 - 2ab*cos(C)\)
In this case, we have side lengths a = 4, b = 5, and c = 7. We want to find the angle C, which is opposite to side c. Substituting these values into the Law of Cosines, we get:
\(7^2 = 4^2 + 5^2\)- 2(4)(5)*cos(C)
49 = 16 + 25 - 40*cos(C)
49 = 41 - 40*cos(C)
40*cos(C) = 41 - 49
40*cos(C) = -8
cos(C) = -8/40
cos(C) = -0.2
To find the measure of angle C, we can take the inverse cosine (arccos) of -0.2:
C = arccos(-0.2)
Using a calculator, we find that C ≈ 101.54 degrees.
Therefore, the measure of the angle between the sides measuring 4 and 5 in the obtuse triangle is approximately 101.54 degrees.
For more such information on: angle
https://brainly.com/question/25716982
#SPJ8
What is 4/12 into decimal form?
Answers
4/12 into decimal form is 0.3
Answer:
4/12 = 0.3333333333...
Step-by-step explanation:
The answer 0.3 is repeated
Hope it helps!
Need answer asap please & thanks

Answers
Tori's pay for the week will be $273.75 .
Tori's per hour earning = $12.50
Suppose Tori work 30 hours a week in her part time job.
Then, Total working hour in a week = 30 Hours
Total earning in a week = $12.50 × 30
= $375
Tax deduction from Tori's paycheck = 27% of Total earning
= 27/100 × 375
= $101.25
Tori's pay for the week = Total earning - Tax deduction
= $375 - $101.25
= $ 273.75
Thus, Tori's pay for the week after deduction of taxes is $273.75.
To learn more about Tax Deduction visit : https://brainly.com/question/12102285
#SPJ9
Help please include explanation screenshot attached and brainliest to correct answer

Answers
Answer:
x>-8 (Or option D)
Step-by-step explanation:
-2x+7<23 Subtract 7 from both sides
-2x<16 Now divide by -2. You also have to flip the < sign because you are dividing by a negative number
x>-8
The reasoning for D over C is because D is an open circle meaning that it is only less than or greater than. When it is a closed circle, it means less than or equal to or greater than or equal to. :)
6. Journalise the following transactions
1. Bricks for Rs 60,000 and timber for Rs 35,000 purchased for
the construction of building. The payment was made by cheque.
2. Placed in fixed deposit account at bank by transfer from current
account Rs 13,000.
3. Appointed Mr. S.N. Rao as Accountant at Rs 300 p.m. and
Received Rs 1000 as security Deposit at 5% p.a. interest.
4. Sold goods to shruti for Rs 80,000 at 15% trade discount and
4% cash discount. Received 75% amount immediately through a
cheque.
5. Purchased goods from Richa for Rs 60,000 at 10% trade
discount and 5% cash discount. 60% amount paid by cheque
immediately.
6.
On 18th jan,Sold goods to shilpa at the list price of Rs 50,000
20% trade discount and 4% cash discount if the payment is made
within 7 days. 75% payment is received by cheque on Jan 23rd.
7. On 25th jan, sold goods to garima for Rs 1,00,000 allowed her
20% trade discount and 5% cash discount if the payment is made
within 15 days. She paid 1/4th of the amount by cheque on Feb 5th
and 60% of the remainder on 15th in cash.
8. Purchased land for Rs 2,00,000 and paid 1% as brokerage and
Rs 15,000 as registration charges on it. Entire payment is made by
cheque.
9. Goods worth Rs 25,000 and cash Rs 40,000 were taken away
by the proprietor for his personal use.
10. Sold goods costing Rs 1,20,000 to charu at a profit of 33% 3 %
on cost less 15% trade discount.
9
11. Paid rent of building Rs 60,000 by cheque. Half the building is
used by the proprietor for residential purpose.
12. Sold goods costing Rs 20,000 to sunil at a profit of 20% on
sales less 20% trade discount .
13. Purchased goods for Rs 1000 from nanda and supplied it to
helen for Rs 1300. Helen returned goods worth Rs 390, which in
turn were returned to nanda.
14. Received invoice at 10% trade discount from rohit and sons
and supplied these goods to madan, listed at Rs 3000.
Answers
1.Bricks and timber purchased for construction. (Debit: Bricks - Rs 60,000, Debit: Timber - Rs 35,000, Credit: Bank - Rs 95,000)
2.Transfer of Rs 13,000 to fixed deposit account. (Debit: Fixed Deposit - Rs 13,000, Credit: Current Account - Rs 13,000)
3.Appointment of Mr. S.N. Rao as Accountant. (Debit: Salary Expense - Rs 300, Debit: Security Deposit - Rs 1,000, Credit: Accountant - Rs 300)
4.Goods sold to Shruti with discounts. (Debit: Accounts Receivable - Shruti - Rs 80,000, Credit: Sales - Rs 80,000)
5.Goods purchased from Richa with discounts. (Debit: Purchases - Rs 60,000, Credit: Accounts Payable - Richa - Rs 60,000)
6.Goods sold to Shilpa with discounts and received payment. (Debit: Accounts Receivable - Shilpa - Rs 50,000, Credit: Sales - Rs 50,000)
7.Goods sold to Garima with discounts and received partial payment. (Debit: Accounts Receivable - Garima - Rs 1,00,000, Credit: Sales - Rs 1,00,000)
8.Purchase of land with additional charges. (Debit: Land - Rs 2,00,000, Debit: Brokerage Expense - Rs 2,000, Debit: Registration Charges - Rs 15,000, Credit: Bank - Rs 2,17,000)
9.Proprietor took goods and cash for personal use. (Debit: Proprietor's Drawings - Rs 65,000, Credit: Goods - Rs 25,000, Credit: Cash - Rs 40,000)
10.Goods sold to Charu with profit and discount. (Debit: Accounts Receivable - Charu - Rs 1,20,000, Credit: Sales - Rs 1,20,000)
11.Rent paid for the building. (Debit: Rent Expense - Rs 60,000, Credit: Bank - Rs 60,000)
12.Goods sold to Sunil with profit and discount. (Debit: Accounts Receivable - Sunil - Rs 24,000, Credit: Sales - Rs 24,000)
13.Purchased goods from Nanda and supplied to Helen. (Debit: Purchases - Rs 1,000, Debit: Accounts Payable - Nanda - Rs 1,000, Credit: Accounts Receivable - Helen - Rs 1,300, Credit: Sales - Rs 1,300)
14.Purchased goods from Rohit and Sons and supplied to Madan. (Debit: Purchases - Rs 2,700, Credit: Accounts Payable - Rohit and Sons - Rs 2,700, Debit: Accounts Receivable - Madan - Rs 3,000, Credit: Sales - Rs 3,000)
Here are the journal entries for the given transactions:
1. Bricks and timber purchased for construction:
Debit: Bricks (Asset) - Rs 60,000
Debit: Timber (Asset) - Rs 35,000
Credit: Bank (Liability) - Rs 95,000
2. Transfer to fixed deposit account:
Debit: Fixed Deposit (Asset) - Rs 13,000
Credit: Current Account (Asset) - Rs 13,000
3. Appointment of Mr. S.N. Rao as Accountant:
Debit: Salary Expense (Expense) - Rs 300
Debit: Security Deposit (Asset) - Rs 1,000
Credit: Accountant (Liability) - Rs 300
4. Goods sold to Shruti:
Debit: Accounts Receivable - Shruti (Asset) - Rs 80,000
Credit: Sales (Income) - Rs 80,000
5. Goods purchased from Richa:
Debit: Purchases (Expense) - Rs 60,000
Credit: Accounts Payable - Richa (Liability) - Rs 60,000
6. Goods sold to Shilpa:
Debit: Accounts Receivable - Shilpa (Asset) - Rs 50,000
Credit: Sales (Income) - Rs 50,000
7. Goods sold to Garima:
Debit: Accounts Receivable - Garima (Asset) - Rs 1,00,000
Credit: Sales (Income) - Rs 1,00,000
8.Purchase of land:
Debit: Land (Asset) - Rs 2,00,000
Debit: Brokerage Expense (Expense) - Rs 2,000
Debit: Registration Charges (Expense) - Rs 15,000
Credit: Bank (Liability) - Rs 2,17,000
9. Goods and cash taken away by proprietor:
Debit: Proprietor's Drawings (Equity) - Rs 65,000
Credit: Goods (Asset) - Rs 25,000
Credit: Cash (Asset) - Rs 40,000
10. Goods sold to Charu:
Debit: Accounts Receivable - Charu (Asset) - Rs 1,20,000
Credit: Sales (Income) - Rs 1,20,000
Credit: Cost of Goods Sold (Expense) - Rs 80,000
Credit: Profit on Sales (Income) - Rs 40,000
11. Rent paid for the building:
Debit: Rent Expense (Expense) - Rs 60,000
Credit: Bank (Liability) - Rs 60,000
12. Goods sold to Sunil:
Debit: Accounts Receivable - Sunil (Asset) - Rs 24,000
Credit: Sales (Income) - Rs 24,000
Credit: Cost of Goods Sold (Expense) - Rs 20,000
Credit: Profit on Sales (Income) - Rs 4,000
13. Goods purchased from Nanda and supplied to Helen:
Debit: Purchases (Expense) - Rs 1,000
Debit: Accounts Payable - Nanda (Liability) - Rs 1,000
Credit: Accounts Receivable - Helen (Asset) - Rs 1,300
Credit: Sales (Income) - Rs 1,300
14. Goods received from Rohit and Sons and supplied to Madan:
Debit: Purchases (Expense) - Rs 2,700 (after 10% trade discount)
Credit: Accounts Payable - Rohit and Sons (Liability) - Rs 2,700
Debit: Accounts Receivable - Madan (Asset) - Rs 3,000
Credit: Sales (Income) - Rs 3,000
for such more question on journal entries
https://brainly.com/question/28390337
#SPJ8
What is the value of y in the equation 4+ y = -3? (1 point)
07
0 1
O-1
0 -7
Answers
What is the surface area?
2 mm
9 mm
3 mm

Answers
Answer:
Surface area of rectangular prism
=P×h
=2(l+w)×h
=2(3+9)×2
=48mm²
\( \boxed{ \frak{Answer}}\)
Given,
Length (l) = 9 mm
Breadth (b) = 3 mm
Height (h) = 2 mm
To find: The surface of it.
We, know that
Surface area of a cuboid = 2(lb + bh + lh)
By using the formula,
= 2(lb + bh + lh)
= 2(9*3 + 3*2 + 9*2)
= 2( 27 + 6 + 18)
= 2(51)
= 102 mm²
Therefore the required surface area is 102 mm²\( \boxed{ \frak{Keep \: Learning }}\)
Find measure angle ACB

Answers
Answer:
87 degrees
ADE ~ ACB (AB is twice the length of AE, AC is twice of AD, CAB and DAE common angle)
So AED and ABC should be equal
11x-2=6x+13
5x=15
x=3
Angle ABC will equal:
6(3)+13= 31 degrees
ACB = 180-31-62
ACB = 87 degrees
The equation m=3b represents the times in minutes (m) it takes a chef to cook a certain number of bacon cheeseburgers (b) A: 3 B: 6 C:1/3 D: 1
Answers
For the given equation:
m = 3b
The constant of proportionality is 3, so the correct option is A.
How to determine the constant of proportionality?
After a small search on the internet, I've found that this question asks for the constant of proportionality.
Remember that a proportional relation is of the form:
y = k*x
Where k is the constant of proportionality, and x and y are the variables.
Here the relation is:
m = 3*b
Where m and b are the variables, then the remaining coefficient is the constant of proportionality, which is 3.
In this way, we can see that the correct option is A.
Learn more about proportional relationships:
https://brainly.com/question/12242745
#SPJ1
In the diagram, the measures of 23 and 27 are 45°. The measure of 25 is
135°. Are lines cand dparallel?
F
5
8
OA. Yes, because 23 and 27 are congruent.
OB. No, because 27 and 25 are not congruent.
C. Yes, because 25 and 27 are supplementary.
D. No, because 23 and 25 are not supplementary.
Answers
The correct answer is D. No because 23 and 25 are not supplementary.
In the given diagram, it is stated that the measures of angles 23 and 27 are 45°, and the measure of angle 25 is 135°. To determine if lines C and D are parallel, we need to analyze the angles formed by these lines.
If the alternate interior angles or corresponding angles are congruent, then the lines are parallel. However, in this case, we don't have enough information about the angles formed by lines C and D to make that determination.
The fact that angle 23 and angle 27 are congruent (both measuring 45°) doesn't provide any information about the relationship between lines C and D. Similarly, the measure of angle 25 being 135° doesn't give us any insight into the parallelism of lines C and D. Therefore, we cannot conclude that lines C and D are parallel based on the given information, and the correct answer is D.
For more such answers on supplementary angle
https://brainly.com/question/12919120
#SPJ8
Study this table.
x
y
–3
–2
–2
0
0
4
4
12
Which best describes the function represented by the data in the table?
linear with a common ratio of 2
linear with a common first difference of 2
quadratic with a common ratio of 2
quadratic with a common first difference of 2
Answers
Consider an arithmetic sequence which has the second term equal to 8 and the fifth term equal to 10. Determine the common difference of this sequence.
Answers
You do know that to get to the fifth term from the second term you had to add the common difference 3 times. (adding ones takes you to the 3d term, adding twice takes you to the 4th term, and adding 3 times takes you to the 5th term.
What is arithmetic sequence?An arithmetic sequence is a sequence where each term increases by adding/subtracting some constant k. This is in contrast to a geometric sequence where each term increases by dividing/multiplying some constant k. Example: a1 = 25. a(n) = a(n-1) + 5.
nth term=a+(n-1)d
Where a is the first term and d is the common difference.
Now,
2nd term=a+(2–1)d=a+ d——————(1)
5th term=a+(5–1)d=a+4d—————-(2)
Now, we take (2)-(1):
5th term-2nd term=(a+4d)-(a+ d)
5th term-2nd term=3d
So:
d=(5th term-2nd term)/3
Now as all the terms are known we can find out the common difference
To learn more about Arithmetic Sequence refers to;
https://brainly.com/question/21730001
#SPJ1
It is estimated that only 68% of drivers wear their safety belt. Part A: What is the probability that exactly 3 drivers are wearing their safety belts if a police officer pulls over five drivers at random? (5 points) Part B: What is the probability the next driver wearing their safety belt that the police officer pulls over is the fifth driver? (5 points) (10 points)
Answers
Hence, there is a 0.68 percent probability that the fifth driver will be the one that police officer summons over while wearing a safety belt.
What does the name probability mean?The word "probability" derives from the Latin word "propitiate," which means "credibility, probability," from the noun probabilism in the 14th century (see probable). The phrase was first used in a mathematical meaning in 1718.
Part A:
The likelihood that precisely 3 drivers are buckled up can be determined using the binomial probability formula:
P(X = 3) = (5 choose 3) × (0.68)³ × (0.32)²
Where (5 choose 3) = 10 is the number of ways to choose 3 drivers out of 5.
P(X = 3) = 10 × 0.68³ × 0.32²
P(X = 3) = 0.267
Consequently, there is a 0.267 percent chance that all 3 drivers are buckled up.
Part B:
The fifth driver will be pulled by by the police officer since 4 other drivers have already been stopped. We are looking for the likelihood that the motorist is wearing a safety belt.
Since 68% of drivers are safety belt wearers, there is a 0.68 percent chance that the following motorist will be as well.
Thus, there is a 0.68 percent chance that the next vehicle the police officer pulls over is driven by a person wearing a safety belt.
To know more about probability visit:
https://brainly.com/question/13604758
#SPJ1
The perimeter of the triangle below is 54 units. Find the value of y.

Answers
Answer:
y = 7
Step-by-step explanation:
3y + (y+1) + (4y-3) = 54
3y + y + 4y + 1 - 3 = 54
8y - 2 = 54
8y = 54 + 2
8y = 56
y = 56/8
y = 7
Check:
3*7 + (7+1) + ((4*7)-3) = 54
21 + 8 + 28-3 = 54
29 + 25 = 54
Use the two given functions to write y as a function of x.
y = -3a + 3, a = -5x + 1
Answers
Answer:
Step-by-step explanation:
To write y as a function of x using the given functions, we can substitute the value of "a" in the first equation with the expression "-5x + 1" from the second equation.
Given:
y = -3a + 3
a = -5x + 1
Substituting the value of "a" in the first equation:
y = -3(-5x + 1) + 3
Now, let's simplify this expression:
y = 15x - 3 + 3
y = 15x
Therefore, y can be expressed as a function of x as:
y = 15x
Identify the level of measurement of the data, and explain what is wrong with the given calculation. In a survey, the favorite sports of respondents are identified as 100 for basketball comma 200 for baseball comma 300 for football comma and 400 for anything else. The average (mean) is calculated for 597 respondents and the result is 256.1 .The data are at the _________________
level of measurement.
Answers
Answer:
The data are at the Nominal level of measurement.
The given calculation is wrong because average (mean) cannot be calculated for nominal level of measurement.
Step-by-step explanation:
The objective here is to Identify the level of measurement of the data, and explain what is wrong with the given calculation.
a)
The data are at the Nominal level of measurement due to the fact that it portrays the qualitative levels of naming and representing different hierarchies from 100 basketball, 200 basketball, 300 football, 400 anything else
b) We are being informed that, the average (mean) is calculated for 597 respondents and the result is 256.1.
The given calculation is wrong because average (mean) cannot be calculated for nominal level of measurement. At nominal level this type of data set do not measure at all , it is not significant to compute their average (mean).
Use the quadratic formula to solve the equation
25x^2-30x+25=0
Answers
Answer: \(x=\frac{3}{5}+i\frac{4}{5},\:x=\frac{3}{5}-i\frac{4}{5}\)
Step-by-step explanation:
\(25x^2-30x+25=0\)
\(x_{1,\:2}=\frac{-\left(-30\right)\pm \sqrt{\left(-30\right)^2-4\cdot \:25\cdot \:25}}{2\cdot \:25}\)
\(\sqrt{\left(-30\right)^2-4\cdot \:25\cdot \:25}\)
\(=\sqrt{30^2-4\cdot \:25\cdot \:25}\)
\(=\sqrt{30^2-2500}\)
\(=i\sqrt{2500-30^2}\)
\(=40i\)
\(x_{1,\:2}=\frac{-\left(-30\right)\pm \:40i}{2\cdot \:25}\)
\(x_1=\frac{-\left(-30\right)+40i}{2\cdot \:25},\:x_2=\frac{-\left(-30\right)-40i}{2\cdot \:25}\)
\(x=\frac{3}{5}+i\frac{4}{5},\:x=\frac{3}{5}-i\frac{4}{5}\)
Mr Hiro's class has 24 students last year, this year it has 16 students.
1. Find the percent of change.
2. Is it a percent of increase or decrease?
Answers
Answer:
33.3% decrease (to 3sf)
Step-by-step explanation:
Percentage decrease = \(\frac{24-16}{24}\) × 100%
= \(\frac{8}{24}\) × 100%
= \(\frac{1}{3}\) × 100%
= 33.3% (to 3sf)
Find the equation of a straight line cutting off the y-intercept 4 from the axis of y and inclined to 60° with the positive direction of X-axis.
Answers
The linear function is given as follows:
\(y = \sqrt{x} + 4\)
How to define a linear function?The slope-intercept equation for a linear function is presented as follows:
y = mx + b
In which:
m is the slope.b is the intercept.The y-intercept is of 4, hence the parameter b is given as follows:
b = 4.
The line is inclined to 60° with the positive direction of X-axis, hence the slope m is given as follows:
m = tan(60º)
\(m = \sqrt{3}\)
Thus the function is given as follows:
\(y = \sqrt{x} + 4\)
More can be learned about linear functions at https://brainly.com/question/15602982
#SPJ1