According to a survey, the probability that a randomly selected worker primarily drives a van to work is 0.868. The probability that a randomly selected worker primarily takes public transportation to work is 0.044.
Answers
Answer:
the probability that a randomly selected worker does neither of these activities is 0.088 or 8.8%.
Step-by-step explanation:
We can use the fact that the sum of probabilities of all possible outcomes must equal 1 to calculate the probability of a randomly selected worker doing neither of these activities.
Let A be the event that a randomly selected worker primarily drives a van to work, and B be the event that a randomly selected worker primarily takes public transportation to work. Then, the probability of neither event happening (i.e., a worker who does not primarily drive a van to work and does not primarily take public transportation to work) is:
P(neither A nor B) = 1 - P(A) - P(B)
Substituting the given probabilities, we get:
P(neither A nor B) = 1 - 0.868 - 0.044 = 0.088
Therefore, the probability that a randomly selected worker does neither of these activities is 0.088 or 8.8%.
Related Questions
Determine whether the graphs of any of the following equations are parallel or perpendicular. Explain
y=4x
x+4y=12
4x+y=1
Answers
Answer:
y=4x and x+4y=12 are perpendicular because they have opposite reciprocal slopes
Step-by-step explanation:
y=4x slope is 4
x+4y=12 slope is -1/4
add 3 and z, then double the result
Answers
Answer:
6+ 2z
Step-by-step explanation:
2(3+z)= 6+ 2z
A construction worker is painting
walls. He has 4 ½ gallons of paint.
All of the walls are the same size and
each require 3/4 gallon of paint. How
many walls will the construction
worker be able to repaint with that
amount of paint?
A.
B.
C.
D.
4 walls
5 walls
6 walls
7 walls
Answers
The construction worker will be able to repaint 6 walls with 4 ½ gallons of paint. Option C
To determine how many walls the construction worker will be able to repaint with 4 ½ gallons of paint, we need to divide the total amount of paint by the amount required per wall.
The worker has 4 ½ gallons of paint, which can be written as 4 + 1/2 gallons.
Each wall requires 3/4 gallon of paint.
To find the number of walls that can be repainted, we divide the total amount of paint by the amount required per wall:
Number of walls = (Total amount of paint) / (Amount required per wall)
Plugging in the values, we have:
Number of walls = (4 + 1/2) gallons / (3/4 gallon)
To simplify the division, we can convert the mixed number 4 1/2 to an improper fraction:
Number of walls = (9/2) gallons / (3/4 gallon)
To divide fractions, we multiply the first fraction by the reciprocal of the second fraction:
Number of walls = (9/2) gallons * (4/3 gallon)
Simplifying the multiplication:
Number of walls = (9 * 4) / (2 * 3) = 36/6 = 6
For more such questions on construction visit:
https://brainly.com/question/27665779
#SPJ8
please answer! Find the value of x that makes a || b

Answers
3. The measure of side c is 121 inches. The measure of side a is 57 inches. What is the length of side b? SHOW YOUR WORK
(Please help)

Answers
The length of the side b is 106. 7 inches
What is the Pythagorean theorem?The Pythagorean theorem can be defined as a mathematical theorem stating that the square of the longest side of a given triangle, called the hypotenuse side is equal to the sum of the square values of the other two sides.
This is represented as;
x² = y² + z²
Such that;
x is the hypotenusey is the adjacent sidez is the opposite sideNow, substitute the values
121² = 57² + b²
find the squares
b² = 14, 641 - 3249
b = √11392
b = 106. 7 inches
Learn about Pythagorean theorem at: https://brainly.com/question/231802
#SPJ1
solve the equation uding the most direct method: 3x(x+6)=-10?
Answers
To solve this problem, you will use the distributive property to create an equation that can be rearranged and solved using the quadratic formula.
DistributeUse the distributive property to distribute 3x into the term (x + 6):
\(3x(x+6)=-10\)
\(3x^2+18x=-10\)
RearrangeTo create a quadratic equation, add 10 to both sides of the equation:
\(3x^2+18x+10=-10+10\)
\(3x^2+18x+10=0\)
Use the Quadratic FormulaThe quadratic formula is defined as:
\(\displaystyle x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)
The model of a quadratic equation is defined as ax² + bx + c = 0. This can be related to our equation.
Therefore:
a = 3b = 18c = 10Set up the quadratic formula:
\(\displaystyle x=\frac{-18 \pm \sqrt{(18)^2 - 4(3)(10)}}{2(3)}\)
Simplify by using BPEMDAS, which is an acronym for the order of operations:
Brackets
Parentheses
Exponents
Multiplication
Division
Addition
Subtraction
Use BPEMDAS:
\(\displaystyle x=\frac{-18 \pm \sqrt{324 - 120}}{6}\)
Simplify the radicand:
\(\displaystyle x=\frac{-18 \pm \sqrt{204}}{6}\)
Create a factor tree for 204:
204 - 1, 2, 3, 4, 6, 12, 17, 34, 51, 68, 102 and 204.
The largest factor group that creates a perfect square is 4 × 51. Therefore, turn 204 into 4 × 51:
\(\sqrt{4\times51}\)
Then, using the Product Property of Square Roots, break this into two radicands:
\(\sqrt{4} \times \sqrt{51}\)
Since 4 is a perfect square, it can be evaluated:
\(2 \times \sqrt{51}\)
To simplify further for easier reading, remove the multiplication symbol:
\(2\sqrt{51}\)
Then, substitute for the quadratic formula:
\(\displaystyle x=\frac{-18 \pm 2\sqrt{51}}{6}\)
This gives us a combined root, which we should separate to make things easier on ourselves.
Separate the RootsSeparate the roots at the plus-minus symbol:
\(\displaystyle x=\frac{-18 + 2\sqrt{51}}{6}\)
\(\displaystyle x=\frac{-18 - 2\sqrt{51}}{6}\)
Then, simplify the numerator of the roots by factoring 2 out:
\(\displaystyle x=\frac{2(-9 + \sqrt{51})}{6}\)
\(\displaystyle x=\frac{2(-9 - \sqrt{51})}{6}\)
Then, simplify the fraction by reducing 2/6 to 1/3:
\(\boxed{\displaystyle x=\frac{-9 + \sqrt{51}}{3}}\)
\(\boxed{\displaystyle x=\frac{-9 - \sqrt{51}}{3}}\)
The final answer to this problem is:
\(\displaystyle x=\frac{-9 + \sqrt{51}}{3}\)
\(\displaystyle x=\frac{-9 - \sqrt{51}}{3}\)
Solve: z5 + 3 = −35
Answers
Answer:
z= - 5 √ 38
Step-by-step explanation:
take the root of both sides
or
you can factor each set and make them equal to zero
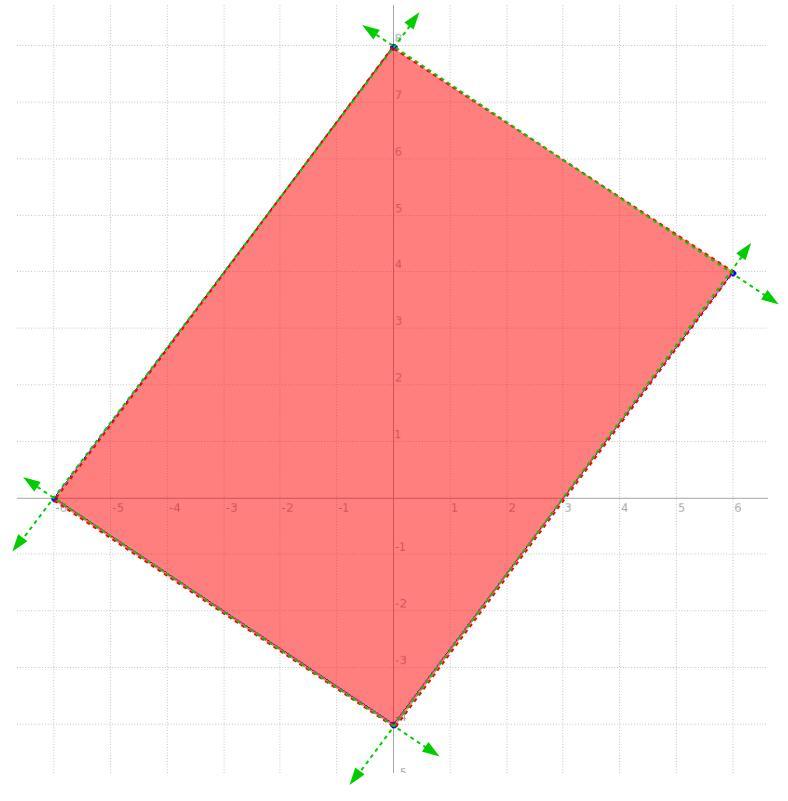
HELP PLEASE I DONT GET THIS

Answers
so the idea being, we have a system of equations of two variables and 4 equations, each one rendering a line, for this case these aren't equations per se, they're INEquations, so pretty much the function will be the same for an equation but we'll use > or < instead of =, but fairly the function is basically the same, the behaviour differs a bit.
we have a line passing through (-6,0) and (0,8), side one
we have a line passing through the x-axis and -6, namely (-6,0) and the y-axis and -4, namely (0,-4), side two
we have a line passing through (0,-4) and (6,4), side three
now, side four is simply the line connecting one and three.
the intersection of all four lines looks like the one in the picture below, so what are those lines with their shading producing that quadrilateral?
well, we have two points for all four, and that's all we need to get the equation of a line, once we get the equation, with its shading like that in the picture, we'll make it an inequality.
\((\stackrel{x_1}{-6}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{8}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{8}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{(-6)}}} \implies \cfrac{8 -0}{0 +6} \implies \cfrac{ 8 }{ 6 } \implies \cfrac{4}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{ \cfrac{4}{3}}(x-\stackrel{x_1}{(-6)}) \implies y -0 = \cfrac{4}{3} ( x +6) \\\\\\ y=\cfrac{4}{3}x+8\hspace{5em}\stackrel{\textit{side one} }{\boxed{y < \cfrac{4}{3}x+8}}\)
\(\rule{34em}{0.25pt}\\\\ (\stackrel{x_1}{-6}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{-4}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{-4}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{(-6)}}} \implies \cfrac{-4 -0}{0 +6} \implies \cfrac{ -4 }{ 6 } \implies - \cfrac{2}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{- \cfrac{2}{3}}(x-\stackrel{x_1}{(-6)}) \implies y -0 = - \cfrac{2}{3} ( x +6) \\\\\\ y=-\cfrac{2}{3}x-4\hspace{5em}\stackrel{\textit{side two} }{\boxed{y > -\cfrac{2}{3}x-4}} \\\\[-0.35em] \rule{34em}{0.25pt}\)
\(\stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{4}-\stackrel{y1}{(-4)}}}{\underset{\textit{\large run}} {\underset{x_2}{6}-\underset{x_1}{0}}} \implies \cfrac{4 +4}{6 -0} \implies \cfrac{ 8 }{ 6 } \implies \cfrac{4}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-4)}=\stackrel{m}{ \cfrac{4}{3}}(x-\stackrel{x_1}{0}) \implies y +4 = \cfrac{4}{3} ( x -0) \\\\\\ y=\cfrac{4}{3}x-4\hspace{5em}\stackrel{ \textit{side three} }{\boxed{y > \cfrac{4}{3}x-4}} \\\\[-0.35em] \rule{34em}{0.25pt}\)
\((\stackrel{x_1}{6}~,~\stackrel{y_1}{4})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{8}) ~\hfill~ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{8}-\stackrel{y1}{4}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{6}}} \implies \cfrac{ 4 }{ -6 } \implies - \cfrac{2}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{4}=\stackrel{m}{- \cfrac{2}{3}}(x-\stackrel{x_1}{6}) \\\\\\ y=-\cfrac{2}{3}x+8\hspace{5em}\stackrel{ \textit{side four} }{\boxed{y < -\cfrac{2}{3}x+8}}\)
now, we can make that quadrilateral a trapezoid by simply moving one point for "side four", say we change the point (0 , 8) and in essence slide it down over the line to (-3 , 4). Notice, all we did was slide it down the line of side one, that means the equation for side one never changed and thus its inequality is the same function.
now, with the new points for side for of (-3,4) and (6,4), let's rewrite its inequality
\((\stackrel{x_1}{-3}~,~\stackrel{y_1}{4})\qquad (\stackrel{x_2}{6}~,~\stackrel{y_2}{4}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{4}-\stackrel{y1}{4}}}{\underset{\textit{\large run}} {\underset{x_2}{6}-\underset{x_1}{(-3)}}} \implies \cfrac{4 -4}{6 +3} \implies \cfrac{ 0 }{ 9 } \implies 0\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{4}=\stackrel{m}{ 0}(x-\stackrel{x_1}{(-3)}) \implies y -4 = 0 ( x +3) \\\\\\ y=4\hspace{5em}\stackrel{ \textit{side four changed} }{\boxed{y < 4}}\)
Find the quotient of 10^-4/10^2
Answers
The quotient of 10⁻⁴/10² is 10⁻⁶
How to Find the quotient of 10⁻⁴/10²?Quotient is the result obtained by dividing one quantity by another. It represents the value that is obtained after division.
For example, if you divide 20 by 2, the quotient is 10 because 20 divided by 2 equals 10.
Division law states that:
10ᵃ / 10ᵇ = 10ᵃ⁻ᵇ
In this case have:
10⁻⁴/10² = 10⁻⁴⁻² (Division law)
10⁻⁴/10² = 10⁻⁶
Learn more about quotient on:
brainly.com/question/27862246
#SPJ1
Simplify Forty eight fourths 48/4
Answers
48 divided by 4 is 12:)
Step-by-step explanation:
48 divided by 4, is 12
or 12/1
Allyson walked 10.8 km to the school. If 1 mile = 1.6 km, about how many miles did she walk?
Answers
Answer:
According to my calculations, 1.6 goes into 10.8 a total of 6 times with a remainder of 1.1999999999999993. If you continue the long division beyond the decimal point, the result would be 6.75.
Step-by-step explanation:
Answer:
6.75 miles
Step-by-step explanation:
1.6 km = 1 mile
1 km = 1/1.6 mile
10.8 km = \(\frac{1}{1.6}*10.8\)
= 6.75 miles
URGENT I NEED HELP FIRST PERSON WHO ANSWERS I'LL GIVE BRAINLYEST
A cylindrical vase has a diameter of 6 inches. At the bottom of the vase, there are 9 marbles, each of diameter 3 inches. The vase is filled with water up to a height of 12 inches.
Which of the following could be used to calculate the volume of water in the vase?
π(3in)2(12in) − 1.5(four over threeπ(9in)3)
π(12in)2(3in) − 1.5(four over threeπ(9in)3)
π(3in)2(12in) − 9(four over threeπ(1.5in)3)
π(12in)2(3in) − 9(four over threeπ(1.5in)3)
Answers
Answer:
C. π(3in)2(12in) − 9(four over threeπ(1.5in)3)Step-by-step explanation:
Volume of water is the difference of volume of vase at 12 in height and the total volume of marbles.
Volume of cylinder up to water level:
Vs = πr²h = π(6/2)²(12) = π×(3 in)²×(12 in)Volume of marbles:
Vm = 9(4/3πr³) = 9×(4/3×π(3/2)³) = 9×(4/3×π×(1.5 in)³)Volume of water:
Vw = Vs - Vm = π×(3 in)²×(12 in) - 9×(4/3×π×(1.5 in)³)Correct choice is C
Answer:
C. π(3in)2(12in) − 9(four over threeπ(1.5in)3)
Step-by-step explanation:
Volume of water is the difference of volume of vase at 12 in height and the total volume of marbles.
Volume of cylinder up to water level:
Vs = πr²h = π(6/2)²(12) = π×(3 in)²×(12 in)
Volume of marbles:
Vm = 9(4/3πr³) = 9×(4/3×π(3/2)³) = 9×(4/3×π×(1.5 in)³)
Volume of water:
Vw = Vs - Vm = π×(3 in)²×(12 in) - 9×(4/3×π×(1.5 in)³)
Correct choice is C
The prior probabilities for events
A1, A2, and A3
are
P(A1) = 0.20,
P(A2) = 0.30,
and
P(A3) = 0.50.
The conditional probabilities of event B given
A1,
A2,
and
A3
are
P(B | A1) = 0.50,
P(B | A2) = 0.30,
and
P(B | A3) = 0.40.
(Assume that
A1, A2, and A3
are mutually exclusive events whose union is the entire sample space.)
(a)
Compute
P(B ∩ A1), P(B ∩ A2), and P(B ∩ A3).
P(B ∩ A1)
=
P(B ∩ A2)
=
P(B ∩ A3)
=
(b)
Apply Bayes' theorem,
P(Ai | B) = P(Ai)P(B | Ai)
P(A1)P(B | A1) + P(A2)P(B | A2) + + P(An)P(B | An),
to compute the posterior probability
P(A2 | B).
(Round your answer to two decimal places.)
(c)
Use the tabular approach to applying Bayes' theorem to compute
P(A1 | B),
P(A2 | B),
and
P(A3 | B).
(Round your answers to two decimal places.)
Events P(Ai)
P(B | Ai)
P(Ai ∩ B)
P(Ai | B)
A1
0.20 0.50 A2
0.30 0.30 A3
0.50 0.40 1.00 1.00
Answers
(a) Through the conditional probability formula:\(P(B ∩ A) = P(B | A) P(A),\)
\(P(B / A1) P(A1) = 0.50 x 0.20 = 0.10A2 = 0.30 x 0.30 = 0.09A3= 0.40 x 0.50 = 0.20\)
(b)Bayes' theorem gives
\(P(A2 | B) = p(B | A2) p(A2) / [p(B | A1) P(A1) + p(B | A2) P(A2) + p(B | A3) p(A3)]= 0.26Thus, P(A2 | B) = 0.26.\)
(c)the tabular approach can show us
Events P(Ai) P(B | Ai) P(Ai ∩ B) P(Ai | B)
A1 0.2 0.5 0.1 0.167
A2 0.3 0.3 0.09 0.307
A3 0.5 0.4 0.2 0.526
Therefore,\(P(A1 | B) = 0.167, p(A2 | B) = 0.307, p(A3 | B) = 0.526.\)
To know more about probabilities
brainly.com/question/30034780
#SPJ4
Find the intervals where the function is increasing and decreasing for the following functions. Using the first derivative test, state which critical value will give you your relative maximum/minimum. You DO NOT have to solve for relative max/min, just the value of c that would give me the min/max based off of the first derivative test.
Answers
f(x) = x^3 - 6x^2 + 12x the function is increasing for x < -2, increasing for x > 4 and decreasing for -2 < x < 4. The critical value that will give you a relative maximum is x = 4. The critical value that will give you a relative minimum is x = -2.
The derivative of the given function is f'(x) = 3x^2 - 12x + 12. Setting this equal to 0 gives us x = 0 and x = 4. By the first derivative test, we can determine that the function is increasing for x < -2, increasing for x > 4 and decreasing for -2 < x < 4. Therefore, the critical value that will give us a relative maximum is x = 4 and the critical value that will give us a relative minimum is x = -2. This can be verified by finding the second derivative of the function, which is f''(x) = 6x -12. Setting this equal to 0 gives us x = 2, which is between the two critical values. Since the second derivative is negative for x < 2, the critical value at x = -2 will give us a relative minimum and since it is positive for x > 2, the critical value at x = 4 will give us a relative maximum.
Learn more about function here
https://brainly.com/question/29633660
#SPJ4
The battery life on Marco's cell phone decreases
according to the scatterplot below. What is the longest
amount of time Marco could use his phone without
charging it?
Answer:

Answers
The longest amount of time that Marco could use his phone without changing the battery is given as follows:
3.3 hours.
How to define a linear function?The slope-intercept representation of a linear function is given by the equation presented as follows:
y = mx + b
The coefficients of the function and their meaning are described as follows:
m is the slope of the function, representing the change in the output variable y when the input variable x is increased by one.b is the y-intercept of the function, which is the initial value of the function, i.e., the numeric value of the function when the input variable x assumes a value of 0. On a graph, it is the value of y when the graph of the function crosses tbe y-axis.In 5 hours, the battery fell from 50% to 20%, hence the slope is given as follows:
-30/5 = -6% an hour.
The battery is currently at 20%, hence the time that Marco could use the phone without charging it is given as follows:
20/6 = 3.3 hours.
More can be learned about linear functions at https://brainly.com/question/24808124
#SPJ1
Use the Midpoint Rule with n = 10 to approximate the length of c(t) = (5 + sin(4t), 6 + sin(7t)) for 0 ≤ t ≤ 2π. (Round your answer to two decimal places.)
Answers
Answer:
34.43
Step-by-step explanation:
A differential of length in terms of t will be ...
dL(t) = √(x'(t)^2 +y'(t)^2)
where ...
x'(t) = 4cos(4t)
y'(t) = 7cos(7t)
The length of c(t) will be the integral of this differential on the interval [0, 2π].
Dividing that interval into 10 equal pieces means each one has a width of (2π)/10 = π/5. The midpoint of pieces numbered 1 to 10 will be ...
(π/5)(n -1/2), so the area of the piece will be ...
sub-interval area ≈ (π/5)·dL((π/5)(n -1/2))
It is convenient to let a spreadsheet or graphing calculator do the function evaluation and summing of areas.
__
The attachment shows the curve c(t) whose length we are estimating (red), and the differential length function (blue) we are integrating. We use the function p(n) to compute the midpoint of the sub-interval. The sum of sub-interval areas is shown as 34.43.
The length of the curve is estimated to be 34.43.

What is the average rate of change for this quadratic
function for the interval from x=2 to x = 4?
A. 12
B. -6
C. -12
D. 6
-10-
Click here for long description
SUBMIT
Answers
The average rate of change of the function over the interval is -6
Finding the average rate of changeFrom the question, we have the following parameters that can be used in our computation:
The graph
The interval is given as
From x = 2 to x = 4
The function is a quadratic function
This means that it does not have a constant average rate of change
So, we have
f(2) = -3
f(4) = -15
Next, we have
Rate = (-15 + 3)/(4 - 2)
Evaluate
Rate = -6
Hence, the rate is -6
Read more about average rate of change at
brainly.com/question/17131025
#SPJ1

What is the slope of the line through (-1, 2) and (-3,-2)?
-5
4
(-1.2)
2
14
1
43 2
- 1
1
2
3
4
-1
2
((-3.2)
3
A. -2
B.
C. 2
D. -

Answers
The answer of the slope or Gradient of the line is 2
A bottle manufacturer has determined that the cost (C) in dollars of producing bottles is C = 0.4x + 1900. What are the
fixed costs (costs incurred even when 0 bottles are produced)?
Answers
Answer:
1,900
Step-by-step explanation:
fixed costs doesn't depend on the value of x in our case they doesn't depend on the value of produced bottles
Solve this system of equations usingthe substitution method.y = 4x3x – 7 = y1

Answers
Given:
\(\begin{gathered} y=4x \\ 3x-7=y \end{gathered}\)Required:
To solve the given equations by using substitution method.
Explanation:
Consider the given two equation
\(\begin{gathered} y=4x------(1) \\ 3x-7=y--------(2) \end{gathered}\)Substitute equation (1) in (2), we get
\(\begin{gathered} 3x-7=4x \\ 3x-4x=7 \\ -x=7 \\ x=-7 \end{gathered}\)Put x in (1), we get
\(\begin{gathered} y=4(-7) \\ \\ y=-28 \end{gathered}\)Final Answer:
\((-7,-28)\)Use the image to determine the direction and angle of rotation.
graph of triangle ABC in quadrant 4 and a second polygon A prime B prime C prime in quadrant 2
90° clockwise rotation
90° counterclockwise rotation
180° clockwise rotation
270° counterclockwise rotation
Answers
The angle of rotation for the described transformation is
180° clockwise rotationHow to know the angle of rotationThe movement or transformation described is form quadrant 4 to quadrant 2.
The transformation will require 180 degrees transformation.
In this type of transformation, both clockwise and the counter clockwise have similar effects
Learn more about angle of rotation at
https://brainly.com/question/2078551
#SPJ1
A test was given to a group of students. The grades and gender are summarized below
A B C Total
Male 3 10 12 25
Female 14 2 13 29
Total 17 12 25 54
If one student is chosen at random from those who took the test,
Find the probability that the student got a 'A' GIVEN they are male.
Answers
The probability that the student got an 'A' given they are male is approximately 0.12 or 12%.
To find the probability that a student got an 'A' given they are male, we need to use Bayes' theorem:
P(A | Male) = P(Male | A) × P(A) / P(Male)
We can find the values of the terms in the formula using the information given in the table:
P(Male) = (25/54) = 0.46 (the proportion of all students who are male)
P(A) = (17/54) = 0.31 (the proportion of all students who got an 'A')
P(Male | A) = (3/17) = 0.18 (the proportion of all students who are male and got an 'A')
Therefore, plugging these values into the formula:
P(A | Male) = 0.18 × 0.31 / 0.46
P(A | Male) ≈ 0.12
So the probability that the student got an 'A' given they are male is approximately 0.12 or 12%.
for such more question on probability
https://brainly.com/question/13604758
#SPJ11
18x + 4
17x + 11
Select the equation you would use to solve for x.
18x + 17x + 11 + 4 = 180
0 18x + 17x = 11 + 4
18x + 4 = 17x + 11

Answers
the answer would be c because the angles are equal to each other
8r/9 - 15 when r = 27
Answers
Answer:
9
Step-by-step explanation:
8x27/9-15
8x27= 216
216/9-15
216/9= 24
24-15=9
=9
Answer:
Your answer is nine
9
can you please help me out if you know this answer

Answers
Step-by-step explanation:
A strike in bowling meant all 10 pins knocked down.
In this case, there is only 1 strike
a number and multiplied by 7?
y + 7
y / 7
y - 7
7y
Answers
its 7y bcs y + 7 is addition,y / 7 is division and y - 7 is subtraction
Select all the correct answers.
Which two factors must Roger consider when calculating the taxable equivalent yield for a municipal bond?
~The bond has a tax-free yield of 5%.
~Roger’s investment income increases an average of 7% each year.
~Roger has realized long-term capital gains that qualify for a tax rate of 0%.
~Roger owns stock that pays a 4% dividend.
~Roger is in the 24% tax bracket.
~Roger was in the 22% tax bracket last year.
Answers
Answer:
The following are what Roger must calculate and put into consideration when calculating the taxable equivalent yield for a municipal bond:
~The bond has a tax-free yield of 5%.
~Roger’s investment income increases an average of 7% each year.
~Roger owns stock that pays a 4% dividend.
~Roger is in the 24% tax bracket.
Step-by-step explanation:
Please help…. Will mark brainliest plus 50 points!!!!

Answers
Answer:
k = 3
Step-by-step explanation:
Expanding the first term, we find 1/x at 10(kx)²(1/x)³ = 10k²/x
Expanding the first term, we find 1/x at 8*1⁷(-2/x)¹ = -16/x
Then
10k² - 16 = 74
k = 3
A car is traveling at a constant speed the graph shows how far the car traveled in miles during a given amount of time
Answers
I NEED BOTH THESE QUESTIONS ANSWERED PLZZZZZZZZZZZZZZZZZZZ

Answers
Answer:
1) 1050 ft squared
2) 200 yards
Step-by-step explanation:
Hope this helps! Pls give brainliest!