A shipping container is in the form of a right rectangular prism, with dimensions of 35 ft by 8 ft by 9 ft 9 in. If the container holds 1420 cubic feet of shipped goods, what percent is full? Round your answer to the nearest whole number if necessary
Answers
Rounded to the nearest whole number, the container is approximately 52% full.
To find the percentage that the shipping container is full, we need to compare the volume of the shipped goods to the total volume of the container.
Given dimensions:
Length = 35 ft
Width = 8 ft
Height = 9 ft 9 in
We need to convert the height to feet by dividing the inches by 12:
Height = 9 ft + (9/12) ft = 9.75 ft
Total volume of the container:
Volume = Length × Width × Height
Volume = 35 ft × 8 ft × 9.75 ft
Volume = 2730 ft³
Volume of the shipped goods:
Given as 1420 ft³
To find the percentage filled, we divide the volume of the shipped goods by the total volume of the container and multiply by 100:
Percentage filled = (Volume of shipped goods / Total volume of container) × 100
Percentage filled = (1420 ft³ / 2730 ft³) × 100
Percentage filled ≈ 52.0%
For more such questions on Volume
https://brainly.com/question/30610113
#SPJ8
Related Questions
Select 3 ratios that are = to 11:1
Answers
Hope this helps
C Solve for x. 8x-4 60°

Answers
Answer:
8
Step-by-step explanation:
8x - 4 = 60
8x = 60 + 4
x = 64/8
x = 8
Pls answer this question as soon as possible

Answers
Answer:
The answer is -½.
✌ yeah it is ✌
Solution Problem 2. (20 points) (a) Show that 125 is the smallest positive integer greater than 100, which can
be expressed in two different ways as a sum of two squares. (b) Find the 20th smallest number that is a sum
of two squares in two different ways. Solution: Problem 3. (20 points)
Answers
(a) 125 is the smallest positive integer greater than 100 that can be expressed in two different ways as a sum of two squares. (b) The 20th smallest number that is a sum of two squares in two different ways is 197.
(a) To show that 125 is the smallest positive integer greater than 100 that can be expressed in two different ways as a sum of two squares, we need to find two distinct pairs of integers (a, b) and (c, d) such that:
125 = a² + b² = c² + d
We can start by listing the squares of integers and checking for sums that equal 125:
1² = 1
2² = 4
3² = 9
4² = 16
5² = 25
6² = 36
7² = 49
8² = 64
9² = 81
10² = 100
From the list, we can see that 125 is not a perfect square. However, we can express it as the sum of two squares in two different ways:
125 = 5² + 10² = 11² + 2²
Therefore, 125 is the smallest positive integer greater than 100 that can be expressed in two different ways as a sum of two squares.
(b) To find the 20th smallest number that is a sum of two squares in two different ways, we can use a systematic approach. We can start with the smallest numbers that can be expressed as a sum of two squares and check if they have multiple representations.
Starting from the smallest non-zero-sum of squares:
1² + 0² = 1
We continue to find more numbers that can be expressed as a sum of two squares:
2² + 1² = 5
1² + 2² = 5
3² + 1² = 10
1² + 3² = 10
4² + 1² = 17
1² + 4² = 17
And so on...
By following this process, we can find the 20th smallest number that can be expressed as a sum of two squares in two different ways:
20th number = 49² + 2² = 7² + 8² = 197
Therefore, the 20th smallest number that is a sum of two squares in two different ways is 197.
To know more about positive integer refer here:
https://brainly.com/question/28165413#
#SPJ11
Multiply.
2x^4 (3x³ − x² + 4x)

Answers
Answer: A
Step-by-step explanation:
When multiplying: Numbers multiply with numbers and for the x's, add the exponents
If there is no exponent, you can assume an imaginary 1 is the exponent
2x⁴ (3x³ − x² + 4x)
= 6x⁷ -2x⁶ + 8x⁵
Answer:
A. \(6x^{7} - 2x^{6} + 8x^{5}\)
Step-by-StepLabel the parts of the expression:
Outside the parentheses = \(2x^{4}\)
Inside parentheses = \(3x^{3} -x^{2} + 4x\)
You must distribute what is outside the parentheses with all the values inside the parentheses. Distribution means that you multiply what is outside the parentheses with each value inside the parentheses
\(2x^{4}\) × \(3x^{3}\)
\(2x^{4}\) × \(-x^{2}\)
\(2x^{4}\) × \(4x\)
First, multiply the whole numbers of each value before the variables
2 x 3 = 6
2 x -1 = -2
2 x 4 = 8
Now you have:
6\(x^{4}x^{3}\)
-2\(x^{4}x^{2}\)
8\(x^{4} x\)
When you multiply exponents together, you multiply the bases as normal and add the exponents together
\(6x^{4+3}\) = \(6x^{7}\)
\(-2x^{4+2}\) = \(-2x^{6}\)
\(8x^{4+1}\) = \(8x^{5}\)
Put the numbers given above into an expression:
\(6x^{7} -2x^{6} +8x^{5}\)
Key Wordsdistribution
variable
like exponents
15.3/0.012=??????????????
Answers
15.3/0.012=??????????????
Answer: 1275
Help me on tangy Tuesday!
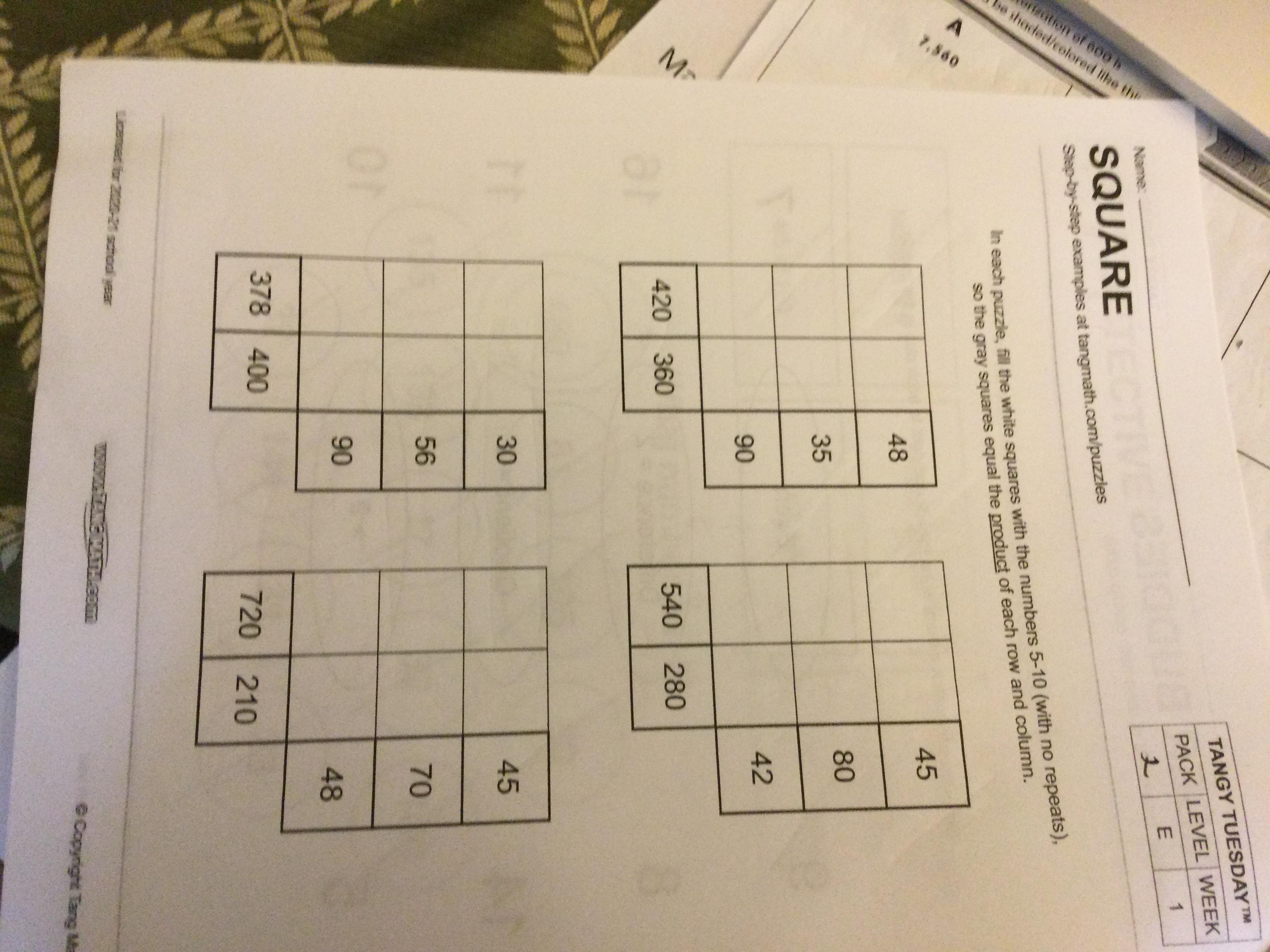
Answers
19
Phil invests £800 for 3 years in a bank account.
The account pays simple interest at a rate of 2% per year.
Work out the total amount of interest Phil has got at the end of 3 years
Answers
Answer:
£4800
Step-by-step explanation:
principal amount:£800
time:3years
rate:2%
amount= principal*rate*time
£800*2*3
=£4800
If the account has 800, .02 times 800 equals 2 percent so doing that 2 percent is 16 and 16 times 3 is the amount of interest he got at the end of 3 years which is 48.
Is the product of 5/7 and 6 less than 6?
Answers
Answer:
yes
Step-by-step explanation:
5/7*6 = 4.28
Answer:
yes
Step-by-step explanation:
5/7×6=4.28
which is less than 6
A student takes a mathematics test scores of 52 and 64. What score on a third test will give the student
an average of 60?
Select one:
A. 60
B. 62
C. 66
D. 64
Answers
Answer:
D. 64
Step-by-step explanation:
Setup an equation to solve for the missing test, x. Since you are doing average and there are three tests, divide the left side of the equation by 3. Set the equation equal to 60 since that is what we want the average to be.
\(\frac{52+64+x}{3}=60\)
Multiply both sides by 3 to remove it from the denominator.
\((3)\frac{52+64+x}{3}=60(3)\)
\(52+64+x=180\)
Simplify and solve for x.
\(52+64+x=180\\116+x=180\\116-116+x=180-116\\x=64\)
Let C=D={-3, -2, -1, 1, 2, 3} and define a relation S from C to D as follows: For all
( x , y ) \in C \times D
(x,y)∈C×D
.
( x , y ) \in S
(x,y)∈S
means that
\frac { 1 } { x } - \frac { 1 } { y }
x
1
−
y
1
is an integer. a. Is 2 S 2? Is -1S-1? Is (3, 3)
\in S ?
∈S?
Is (3, -3)
\in S ?
∈S?
b. Write S as a set of ordered pairs. c. Write the domain and co-domain of S. d. Draw an arrow diagram for S.
Answers
Answer:
Step-by-step explanation:
I'm pretty
a. Let's check whether the given pairs are in the relation S or not.
Is 2 S 2?
To check if (2, 2) is in S, we need to evaluate the expression:
(1/2) - (1/2) = 1/2 - 1/2 = 0
Since 0 is an integer, (2, 2) is in S.
Is -1 S -1?
To check if (-1, -1) is in S, we need to evaluate the expression:
(1/-1) - (1/-1) = -1 - (-1) = 0
Since 0 is an integer, (-1, -1) is in S.
Is (3, 3) ∈ S?
To check if (3, 3) is in S, we need to evaluate the expression:
(1/3) - (1/3) = 1/3 - 1/3 = 0
Since 0 is an integer, (3, 3) is in S.
Is (3, -3) ∈ S?
To check if (3, -3) is in S, we need to evaluate the expression:
(1/3) - (1/-3) = 1/3 + 1/3 = 2/3
2/3 is not an integer, so (3, -3) is not in S.
b. Set of ordered pairs S:
S = {(x, y) | (1/x) - (1/y) is an integer}
S = {(2, 2), (-1, -1), (3, 3)}
c. Domain and Co-domain of S:
Domain of S: The set of all first components (x-values) of the ordered pairs in S.
Domain of S = {-3, -2, -1, 1, 2, 3}
Co-domain of S: The set of all second components (y-values) of the ordered pairs in S.
Co-domain of S = {-3, -2, -1, 1, 2, 3}
d. Arrow diagram for S:
Domain (C): {-3, -2, -1, 1, 2, 3}
Co-domain (D): {-3, -2, -1, 1, 2, 3}
(2, 2) -----> (0) // 0 represents an integer
(-1, -1) -----> (0)
(3, 3) -----> (0)
(3, -3) -----> (2/3) // 2/3 is not an integer
Note: The arrow diagram helps visualize the mapping of elements from the domain to the co-domain based on the relation S. Arrows point from the element in the domain to the result of the expression (integer or not integer) in the co-domain.
To know more about integer here
https://brainly.com/question/929808
#SPJ2
7. Define a variable and write an expression for the phrase.
the quotient of 2 times a number and 19
2x/19
38x
19x/2
X/38
Answers
if Maya drove 30 laps in six minutes how many laps did she drive in one minute
Answers
Answer:
5 laps in one minute.
Step-by-step explanation:
1. Divide 30, the number of laps, by 6, the number of minutes. So, for every 1 minute Maya drives on lap.
PLEASE HELP!!
Fill in the blank. In the triangle below, x =_____. Round your answer to two decimal places.

Answers
Answer:
Step-by-step explanation:
Using Trigonometry: SOH CAH TOA,
tan (47°) = x/35Cross multiplying:
x = tan (47°) × 35
= 37.5329
= 37.53 to two decimal places
ASAP! I WILL GIVE BRAINLEST
The satellite dish is shaped like a paraboloid of revolution. This means that it can be formed by rotating a parabola around its axis of symmetry. The receiver is to be located at the focus. If the dish is 72 feet across at its opening and 9 feet deep at its center, where should the receiver be placed?
Find the equation of the parabola.
How far above the vertex should the receiver be placed?
Answers
Answer:
45 feet
Step-by-step explanation:
The parabola that forms the shape of the satellite dish has its axis of symmetry along the vertical direction, and the vertex at the bottom center of the dish. Let's assume that the vertex of the parabola is at the origin (0,0) of a coordinate system, and the opening of the dish is along the x-axis. Then the equation of the parabola is:
y = a x^2
where "a" is a constant that determines the shape of the parabola. We can find the value of "a" using the given dimensions of the dish.
At the opening of the dish, which has a diameter of 72 feet, the y-coordinate is zero. Therefore, we have:
0 = a (36)^2
Solving for "a", we get:
a = 0
This means that the equation of the parabola is simply y = 0, which is a horizontal line passing through the origin. Clearly, this is not the correct equation for the parabola.
To find the correct equation, we need another point on the parabola. We are given that the depth of the dish at its center, which corresponds to the focus of the parabola, is 9 feet. Using the definition of a parabola, we know that the distance from any point on the parabola to the focus is equal to the distance from that point to the directrix. Since the axis of symmetry is vertical, the directrix is a horizontal line located 9 feet below the vertex.
The equation of the directrix is therefore:
y = -9
We can use this to find another point on the parabola. Consider a point (x,y) on the parabola that is equidistant from the focus (0,9) and the directrix y = -9. The distance from (x,y) to the focus is:
d = sqrt(x^2 + (y-9)^2)
The distance from (x,y) to the directrix is simply y + 9. Therefore, we have:
sqrt(x^2 + (y-9)^2) = y + 9
Squaring both sides and simplifying, we get:
x^2 = 4y(18-y)
This is the equation of the parabola. We can now find the x-coordinate of the receiver, which is located at the focus (0,9). Setting y = 9 in the equation of the parabola, we get:
x^2 = 4(9)(9) = 324
Therefore, the x-coordinate of the receiver is:
x = ±18
Since the dish is 72 feet across at its opening, the receiver should be located at a distance of 36 feet from the center of the dish. Therefore, the receiver should be placed at a height of:
y = 9 + 36 = 45 feet
above the vertex of the parabola.
Find the length of BC

Answers
Answer: 48
The length of AC is the same of BC.
So, the sides will have the same length.
AC is 48, so BC will also be 48.
The answer to the question is 48.
Given triangle PQS and triangle PRM find RM.
Please explain I need it fast.

Answers
The value of RM is 12
What are similar triangles?Similar triangles have the same corresponding angle measures and proportional side lengths.
The corresponding angles of similar triangles are equal.
Also the ratio of corresponding sides of similar triangles are equal.
Since triangle PQS and triangle PRM are similar then;
represent RM by x
6/8 = 9/x
6x = 72
x = 72/6
x = 12.
The value of RM is 12.
learn more about similar triangles from
https://brainly.com/question/14285697
#SPJ1
can someone help wit this geometry question plz pic below

Answers
Answer:
C. ΔGTA ≅ ΔQME
good luck, i hope this helps :)
Kayla earns 80.00 per day at her job and spends 4.00 per day on transportation. What set of integers best represents these values?
Answers
What are the domain and range of the function? the domain is the set of integers, and the range is y > 4. The domain is the set of integers, and the range is y > 0. The domain is the set of real numbers, and the range is y > 0. The domain is the set of real numbers, and the range is y > 4.
Answers
The correct option is (D) "The range is y > 0, and the domain is all real integers."
What are domain and range?In order to identify the values of the independent variable x and acquire the domain, we simply solve the equation y = f(x).
Simply put, x=g(y) will calculate the function's range after we identify g's domain (y).
So, the domain and range of the graph are calculated as follows:
The interval (-,) is the domain of the graph's function: (-∞,∞)
That implies: Real numbers only
The interval between (0,) is the range of the graph's function: (0,∞)
It implies that y>0 is true for all positive real values.
Therefore, the correct option is (D) "The range is y > 0, and the domain is all real integers."
Know more about the domain and range here:
https://brainly.com/question/2264373
#SPJ4
Correct question:
What are the domain and range of the function on the graph?
A)The domain includes all integers, and the range is y ≥ 0.
B)The domain includes all integers, and the range is y > 0.
C)The domain includes all real numbers, and the range is y ≥ 0.
D)The domain includes all real numbers, and the range is y > 0.

(a) if tan∅ = 8/15, find the value of
sin∅ + cos∅(1- cos∅) (b)The angle of elevation of the top of a radio mask from a point due east of it and 96m away from its base is 30degrees. From another point, due west of the mask, the angle of elevation of the top is 60degrees. Calculate the distance of the second point from the base of the mast.
Answers
Answer:
Below in bold.
Step-by-step explanation:
The right triangle of which ∅ is a part has
Hypotenuse = sqrt(8^2 + 15^2)
= sqrt289
= 17,
So, sin ∅ = 8/17 and cos ∅ = 15/17
and
sin∅ + cos∅(1- cos∅)
= 8/17 + 15/17(1 - 15/17)
= 8/17 + 15/17 - 225/289
= 166/289.
(b) tan 30 = h/96 where h is height of the mast
h = 96 tan 30.
= 55.4256
tan 60 = 55.4256/d where d is the required distance
d = 55.4256/ tAN60
= 32 M
Describe fully the graph which has equation x² + y² = 9
Answers
Answer:
Center: (0,0)
Radius: 3
Graph:
Please find attachment to view the graph.
Step-by-step explanation:
Please give the brainliest.

Determine the interest on the following notes: (Use 360 days for calculation.) (a) $5,600 at 5% for 90 days. $ (b) $1,280 at 9% for 5 months. $ (c) $6,900 at 8% for 60 days. $ (d) $2,000 at 7% for 6 months. $
Answers
Therefore, the interest on the notes would be:(a) $70 (b) $45 (c) $92 (d) $70.
To determine the interest on the given notes, we can use the simple interest formula:
Interest = Principal * Rate * Time
(a) For $5,600 at 5% for 90 days:
Principal = $5,600, Rate = 5% (or 0.05), Time = 90 days/360 (converted to years)
Interest = $5,600 * 0.05 * (90/360) = $70
(b) For $1,280 at 9% for 5 months:
Principal = $1,280, Rate = 9% (or 0.09), Time = 5 months/12 (converted to years)
Interest = $1,280 * 0.09 * (5/12) = $45
(c) For $6,900 at 8% for 60 days:
Principal = $6,900, Rate = 8% (or 0.08), Time = 60 days/360 (converted to years)
Interest = $6,900 * 0.08 * (60/360) = $92
(d) For $2,000 at 7% for 6 months:
Principal = $2,000, Rate = 7% (or 0.07), Time = 6 months/12 (converted to years)
Interest = $2,000 * 0.07 * (6/12) = $70
To know more about interest,
https://brainly.com/question/32731542
#SPJ11
Please help! (look at the image below!!)

Answers
The numbers arranged in order from least to greatest is: √146, 12.39, 12.62, 12⅝, and 12¾. The third option is correct.
What is ordering of numbersThe ordering of numbers refers to arranging numbers in a specific sequence based on their magnitude or value. The ordering of numbers is determined by their relative values. Comparisons are made between numbers to determine their position in the order.
12⅝ = 101/8 = 12.645
12.62 = 12.62
√146 = 12.0830
12.39 = 12.39
12¾ = 51/4 = 12.75
Therefore, the numbers arranged in order from least to greatest is: √146, 12.39, 12.62, 12⅝, and 12¾.
Read more about numbers here:https://brainly.com/question/1094377
#SPJ1
Pls someone help me with thissss plsss

Answers
Answer:
y = 5x -3
Step-by-step explanation:
slope = 5
y int = -3
Help me with answer asp



Answers
Answer:
picture #1 - 50.27 square units
picture #2 - 113.10 square units
picture #3 - 380.13 square units
Step-by-step explanation:
picture #1 - area = πr^2 -> π*4^2 = 50.27 square units
picture #2 - area = πr^2 -> π*6^2 = 113.10
picture #3 - area = πr^2 -> π*11^2 = 380.13
A couple plans to save for their child’s college education. What principle must be deposited by the parents when their child is born to have $43,000 when their child reaches the age of 18 assume the money earned 8% interest compounded quarterly round your answer to the nearest decimal
Answers
SOLUTION
We will apply the amount formula
\(\begin{gathered} A=P(1+\frac{r}{n})^{nt} \\ \text{Where } \\ A\text{ = amount = }43,000\text{ dollars } \\ P=pri\text{ncipal money deposited }=\text{ ?} \\ r=\text{interest rate = 8}\%=0.08 \\ n\text{ = number of times compounded = quarterly = 4} \\ t=\text{ time in years = 18years } \end{gathered}\)Substituting each into the equation, we have
\(\begin{gathered} A=P(1+\frac{r}{n})^{nt} \\ 43,000=P(1+\frac{0.08}{4})^{4\times18} \\ 43,000=P(1.02)^{72} \\ 43,000=4.161140375P \\ P=\frac{43,000}{4.161140375} \\ P=10,333.7056972 \end{gathered}\)Hence the answer is $10,333.71 to two decimal places
In a bar graph the length of the bar need not be in proportion to the information being shown.
True
False
Answers
In a bar graph the length of the bar need not be in proportion to the information being False.
Bar graph. A bar chart is frequently used to compare values of different things at a specific time. It presents information visually using rectangles (bars). It generally serves as a visual aid for proportions, patterns, comparisons, and contrasts.
How do you describe a bar graph?To represent value, it makes use of bars that stretch to various heights. Vertical bars, horizontal bars, grouped bars (several bars that compare values in a category), and stacked bars can all be used to construct bar graphs (bars containing multiple types of information).
A relationship is proportionate if its graph is a line or ray that passes through the origin. It is not proportionate if the line or ray does not go through the origin. Additionally, something is not proportionate if it is not linear.
comparisons of several variables that are simple. clarity in the presentation of data trends. Simple value determination.
To learn more about bar graph refer to:
https://brainly.com/question/24741444
#SPJ1
abc is a right triangle with ab=ac. bisector of <a meets bc at d. prove that bc = 2ad.
Answers
Answer:
Let ac=ab=5
With this, bc= 5√2
Step-by-step explanation:
So to find ad, Let ad be x
5√2=(2)(x)
(5√2/2)= x
This proves that bc=2ad

!50 POINTS!
Which number is a solution of the inequality?
6 greater than z left-parenthesis 10 minus z right-parenthesis
A. 0
B. 1
C. 2
D. 3
I'm super confused on this question. Awarding Brainiest for Answer and Step By Step Explanation. Thanks!
Answers
Answer:
A. 0Step-by-step explanation:
Given inequality:
6 > z(10 - z)Solution:
6 > 10z - z²z² - 10z + 6 > 0z² - 10z + 25 > 19(z - 5)² > 19z - 5 > √19 ⇒ z > 5 + √19 ⇒ z > 9.35z - 5 < - √19 ⇒ z < 5 - √19 ⇒ z < 0.64The only number satisfying this inequality is 0.
Correct choice is A