A ramp goes from a doorway of a building to the ground. The end of the ramp connected to the doorway is 1 foot above the ground. The distance along the ramp to the building is 5 feet. What is the angle of elevation of the ramp to the nearest degree?
A. 11°
B. 0°
C. 12°
D. 1°

Answers
Using the trigonometry ratio, he angle of elevation of the ramp to the nearest degree is 11°.
In the given question,
A ramp goes from a doorway of a building to the ground.
The end of the ramp connected to the doorway is 1 foot above the ground.
The distance along the ramp to the building is 5 feet.
We have to find the angle of elevation of the ramp to the nearest degree.
The distance is 5 feet.
The height is 1 foot.
To find the angle of elevation we used the trigonometry ratio.
According the trigonometry ratio, we know that tangent is the ratio between height and distance.
We can write it as
tan A=height/distance
Now putting the value
tan A=1/5
tan A=0.2
So A = arctan(0.2)
A = 11.30°
A ≈ 11°
Hence, the angle of elevation of the ramp to the nearest degree is 11°.
To learn more about trigonometry ratio link is here
brainly.com/question/28820002
#SPJ1
Related Questions
3m + n = 71
2m - n = 30
Answers
Answer:
m = 20.2; n = 10.4
Step-by-step explanation:
\(\left \bigg \{ { \big {3m + n = 71} \atop \big {2m - n = 30}} \right.; => \left \bigg \{ { \big {3m + n -3m= 71-3m} \atop \big {2m - n-2m = 30-2m}} \right.; => \left \bigg \{ { \big { n = 71-3m} \atop \big { - n = 30-2m}} \right. ; => \\\\=> \left \bigg \{ { \big { n = 71-3m} \atop \big { - n \times (-1) = (30-2m)\times (-1)}} \right.; =>\left \bigg \{ { \big { n = 71-3m} \atop \big { n = -30+2m}} \right..\)
-30 + 2m = 71 - 3m
-30 + 2m + 30 = 71 - 3m + 30
2m = 101 - 3m
2m + 3m = 101 - 3m + 3m
5m = 101
5m ÷ 5 = 101 ÷ 5
m = 20.2
n = 71 - 3m = 71 - 3 × 20.2 = 10.4
Which statement about the quadratic equation below is true?
-1.5x2 +54 = 0
A The equation has X = 6 as its only solution.
B The equation has no real solutions.
C The equation has an infinite number of solutions.
D The equation has x = 6 and x = -6 as its only solutions.
Answers
Answer:
x = ± 6
Step-by-step explanation:
1: Subtract both sides by -54
\(-1.5x^2=-54\)
2: Divide both sides by -1.5
\(x^2=36\)
3: Take both sides to the 1/2 power
\(x= 6, -6\)
Bentley invested $430 in an account paying an interest rate of 2.5% compounded continuously. Assuming no deposits or withdrawals are made, how long would it take, to the nearest year, for the value of the account to reach $510?
Answers
Answer:
its 11
Step-by-step explanation:
Answer:
7
Step-by-step explanation:
Consider a comparison of two models. The "complete" model has both curvature and interaction. The "reduced" model has curvature, but no interaction. You compare the two models using a nested (subset) F-test and determine that you should "reject H0 ". True or False: The reduced model fits the data better than the complete model. Group of answer choicesTrueFalse
Answers
Answer:
True
Step-by-step explanation:
The reduced model and complete are the two models that can be used to determine test the hypothesis. The best way to determine which model fits the data set is to determine the F-test. The Full model is unrestricted model whereas reduced model is restricted model. F-test determines which model to choose for hypothesis testing for better and accurate results.
Use the graph of f(x) to find the solutions to the equation f(x)=0.

Answers
Answer:
x = -4, 7
Step-by-step explanation:
Pre-SolvingWe are given the graph of the function f(x), and we want to find the values that make the statement f(x) = 0.
f(x) = 0 means that there are certain values that make the value of f(x) (which can be considered as y) equal to 0.
SolvingWe can look to the graph to help us - we should look at where y is equal to 0, which is the x-axis.
On the x-axis, we can see that the function passes through both -4 and 7 (the graph goes up by 1) on that line.
As coordinate points, they are written as (-4,0) and (7,0).This means that when either -4 or 7 are substituted into the function (i.e. when they are equal to x), they will make the function equal 0.
So, it means that x = -4, 7.
what theorem can be used to probe the 2 triangles similar?
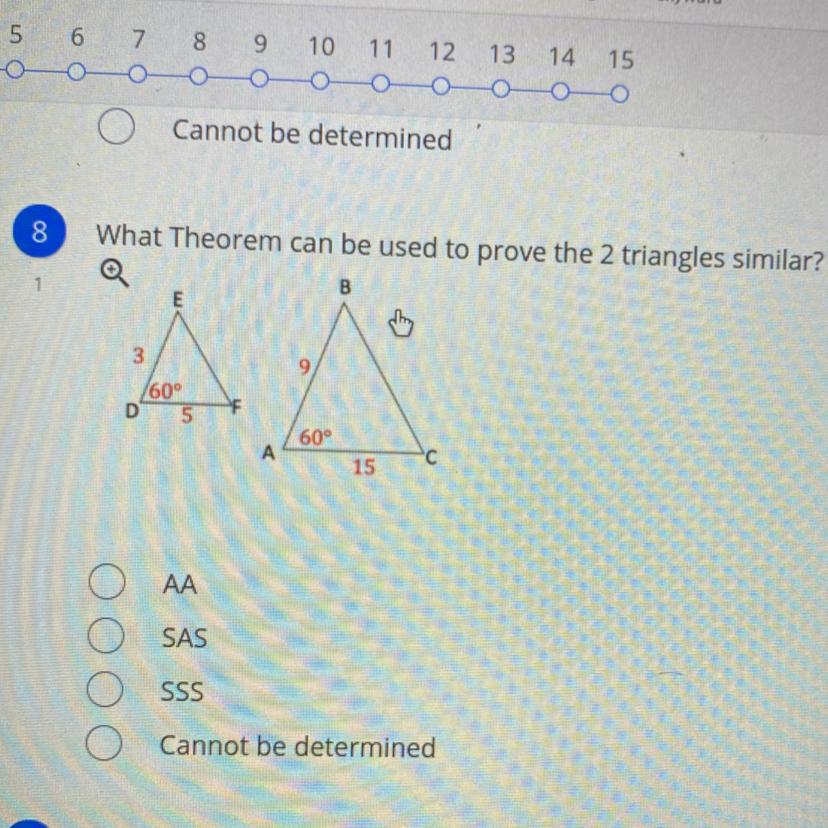
Answers
Answer:
B. SAS
Step-by-step explanation:
Two sides of ∆DEF (DE and DF) are proportional to two corresponding sides of ∆ABC (AB and AC), and also their included angles (<D and <A) are equal to each other.
Therefore, based on the SAS criterion, both triangles are proven to be similar to each other.
Both triangles satisfy the SAD Criterion, and hence, they can be proven to be similar to each other.
The total number of cats and dogs at the shelter is 125.
There are 5 more cats than dogs,
Answers
Answer:
UH
Step-by-step explanation:
25
In a certain Algebra 2 class of 28 students, 14 of them play basketball and 19 of them play baseball. There are 5 students who play neither sport. What is the probability that a student chosen randomly from the class plays basketball or baseball?
Answers
Answer:
23/28 (82.1%)
Step-by-step explanation:
See attached Venn Diagram
23 out of 28 play basketball or baseball

A little girl and a little boy stop to each buy a tablet of chocolate. But the little girl is missing 10 cents to pay and the little boy is missing 1 cent. They then decide to buy a tablet together. But they are still missing 1 cent. How much does the chocolate bar cost?
Answers
The chocolate bar costs 9 cents. The little girl is missing 10 cents and the little boy is missing 1 cent, so together they are missing 11 cents.
What is cost?Cost is a monetary measure of the amount of resources, such as time or money, that must be expended to produce a product or service. It is a fundamental factor of economic production, as it is necessary to make products and services available to consumers. Cost can be determined in a variety of ways and can be linked to economic theory through the concept of opportunity cost. In business, cost is a major factor in decisions related to production, pricing, and marketing. Cost is also a factor in accounting and budgeting, as it is necessary to track and report the costs of organizational operations.
The chocolate bar costs 9 cents. The little girl is missing 10 cents and the little boy is missing 1 cent, so together they are missing 11 cents. If the chocolate bar cost 9 cents, that would leave 1 cent for them to split.
To learn more about cost
https://brainly.com/question/2292799
#SPJ1
Please help with this question.

Answers
Answer:
3m+20>35
Explanation
m stands for months 3 every m
+ the 20 he starts with will be grater than >35
The table values of two linear functions is given below.if they intersect at the point (a,b) what is the value of a+b
-2. - 1. 1. 2.

Answers
Answer:
Step-by-step explanation:
Here is a more detailed explanation:
We are given two linear functions, f(x) and g(x), and their values for x = 1 and x = 4:
x f(x) g(x)
1 3 5
4 9 20
To find the value of a + b at the point of intersection (a, b) of the two functions, we need to first find the equations of the two functions. To do this, we need to find the slope and y-intercept of each function.
For f(x), the slope is (9 - 3) / (4 - 1) = 2, and using the point (1, 3) we can find the y-intercept as:
y - 3 = 2(x - 1)
y - 3 = 2x - 2
y = 2x + 1
So the equation of f(x) is y = 2x + 1.
Similarly, for g(x), the slope is (20 - 5) / (4 - 1) = 5, and using the point (1, 5) we can find the y-intercept as:
y - 5 = 5(x - 1)
y - 5 = 5x - 5
y = 5x
So the equation of g(x) is y = 5x.
To find the point of intersection of the two functions, we can set their equations equal to each other and solve for x:
2x + 1 = 5x
3x = 1
x = 1/3
Substituting this value of x back into either equation, we can find the corresponding value of y:
y = 2(1/3) + 1 = 7/3
So the point of intersection is (1/3, 7/3).
Therefore, a + b = 1/3 + 7/3 = 8/3. This is approximately equal to 2.67. The answer closest to this value is -1, so the correct answer is (b) -1.
Learning Task 3:
Solve.
1. What is the area of the rectangle whose length is (x + 5) and width (x - 5)?
2. What is the area of the square whose sides measure (3x + 4)?
3. The area of the rectangle is 3x2 + 7x - 6, what is the length if the width is
(x + 3)
4. What is the average speed of the car that covers a distance of
(2y3-7y2 + 5y - 1) km in (2y-1) hour?
5. Multiply (m2 + 2m-2) by the sum of (m + 3 ) and (2m - 3)
Answers
Answer:
\(Area = x^2- 25\)
\(Area =9x^2 +24x + 16\)
\(Length = (3x -2)\)
\(Speed = \left(y^2-3y+1\right)\)
\(Product = 3m^3 + 6m^2 - 6m\)
Step-by-step explanation:
Solving (1):
\(Length = (x + 5)\)
\(Width = (x - 5)\)
Required
Calculate Area
\(Area = Length * Width\)
\(Area = (x + 5) * (x - 5)\)
\(Area = x^2 + 5x - 5x - 25\)
\(Area = x^2- 25\)
Solving (2):
Given
\(Length = (3x + 4)\)
Required: Calculate Area
\(Area =Length * Length\)
\(Area =(3x + 4) * (3x + 4)\)
\(Area =9x^2 + 12x + 12x + 16\)
\(Area =9x^2 +24x + 16\)
Solving (3):
\(Area = 3x^2 + 7x - 6\)
\(Width = x + 3\)
Required: Calculate Length
\(Area = Length * Width\)
\(Length = \frac{Area}{Width}\)
\(Length = \frac{3x^2 + 7x - 6}{x + 3}\)
Factorize the numerator
\(Length = \frac{3x^2 + 9x -2x - 6}{x + 3}\)
\(Length = \frac{3x(x + 3) -2(x + 3)}{x + 3}\)
\(Length = \frac{(3x -2) (x + 3)}{x + 3}\)
Divide by x + 3
\(Length = (3x -2)\)
Solving (4):
\(Distance = (2y^3 - 7y^2 + 5y -1)\)
\(Time = 2y - 1\)
Required: Determine the average speed
This is calculated as:
\(Speed = \frac{Distance}{Time}\)
\(Speed = \frac{2y^3 - 7y^2 + 5y -1}{2y - 1}\)
Factorize the numerator
\(Speed = \frac{\left(2y-1\right)\left(y^2-3y+1\right)}{2y - 1}\)
\(Speed = \left(y^2-3y+1\right)\)
Solving (5):
Multiply \((m^2 + 2m - 2)\) by sum of \((m + 3)\) and \((2m - 3)\)
First, calculate the sum:
\(Sum = m + 3 + 2m - 3\)
\(Sum = m + 2m+3 - 3\)
\(Sum = 3m\)
Then, the product
\(Product = (m^2 + 2m - 2)(3m)\)
\(Product = 3m^3 + 6m^2 - 6m\)
Answer:
Step-by-step explanation:
Solving (1):
Required
Calculate Area
Solving (2):
Given
Required: Calculate Area
Solving (3):
Required: Calculate Length
Factorize the numerator
Divide by x + 3
Solving (4):
Required: Determine the average speed
This is calculated as:
Factorize the numerator
Solving (5):
Multiply by sum of and
First, calculate the sum:
Then, the product
Which answer choice shows the equation below in slope intercept form?
8x – 3y = –24

Answers
solve pls brainliest

Answers
Answer:
38.8
Step-by-step explanation:
Because 6 is 5 and higher so it rounds up
Answer:
38.8
Step-by-step explanation:
in 38.765 the number 7 is in the tenths place so you if the number to the right of it is 5or bigger you turn the 7 into an 8
Can you give me the right answers please

Answers
Step-by-step explanation:
150 is base pay
5 is pay per shoe
From the top of a lighthouse 82 m tall, a guard sees two ships at sea.
The angle of depression to the closer ship is 53° and to the further ship is 39°.
How far are the ships apart from each other to the nearest metre?

Answers
The distance between the two ship based on the angle of depression is 42 meters.
The distance of each ship can be calculated thus:
TanX = opposite / Adjacent
The first ship:
Tan53 = distance/ 82
distance= 108.82 meters
The second ship:
Tan39 = distance/ 82
distance= 66.40 meters
The Difference between the ships are :
108.82 - 66.40 = 42.42 metersTherefore, the distance between the two ships is 42 meters.
Learn more on angles of depression:https://brainly.com/question/17193804
#SPJ1
What’s the answer to this

Answers
2. The route used by a certain motorist in commuting to work contains two intersections with traffic signals. The probability that he must stop at the first signal is 0.36, the analogous probability for the second signal is 0.54, and the probability that he must stop at at least one of the two signals is 0.65. What is the probability that he must stop at exactly one signal?
Answers
Answer:
0.30
Step-by-step explanation:
Probability of stopping at first signal = 0.36 ;
P(stop 1) = P(x) = 0.36
Probability of stopping at second signal = 0.54;
P(stop 2) = P(y) = 0.54
Probability of stopping at atleast one of the two signals:
P(x U y) = 0.6
Stopping at both signals :
P(xny) = p(x) + p(y) - p(xUy)
P(xny) = 0.36 + 0.54 - 0.6
P(xny) = 0.3
Stopping at x but not y
P(x n y') = P(x) - P(xny) = 0.36 - 0.3 = 0.06
Stopping at y but not x
P(y n x') = P(y) - P(xny) = 0.54 - 0.3 = 0.24
Probability of stopping at exactly 1 signal :
P(x n y') or P(y n x') = 0.06 + 0.24 = 0.30
In △JKL , if m∠ J < 90° , then ∠K and ∠L are _____
Answers
Both angle K and angle L must be acute angles, measuring less than 90 degrees, in order to satisfy the conditions of the given triangle.
In triangle JKL, if angle J is less than 90 degrees, then angle K and angle L are both acute angles.
An acute angle is defined as an angle that measures less than 90 degrees. Since angle J is given to be less than 90 degrees, it is an acute angle.
In a triangle, the sum of the interior angles is always 180 degrees. Therefore, if angle J is less than 90 degrees, the sum of angles K and L must be greater than 90 degrees in order to satisfy the condition that the angles of a triangle add up to 180 degrees.
Hence, both angle K and angle L must be acute angles, measuring less than 90 degrees, in order to satisfy the conditions of the given triangle.
For more questions on triangle
https://brainly.com/question/1058720
#SPJ8
NEED THE ANSWERS FAST PLEASE
In Exercises 13 and 14, find a possible pair of integer values for a and c so that
the quadratic equation has the given number and type of solution(s). Then write
the equation.
13. ax² − 3x + c = 0; two real solutions
-
14. ax² + 10x + c = 0; two imaginary solutions
15. Determine the number and type of solutions to the equation 2x² - 8x = -15.
A. two real solutions
B. one real solution
C. two imaginary solutions
D. one imaginary solution
In Exercises 16 and 17, use the Quadratic Formula to write a quadratic equation
that has the given solutions.
16. x
10 ± √√-68
14
17. x =
-3±i√√7
8
In Exercises 18-21, solve the quadratic equation using the Quadratic Formula.
Then solve the equation using another method. Which method do you prefer?
Explain.
18. 7x² + 7 = 14x
20. x² + 2 = -x
19. x² + 20x = 8
21. 8x² - 48x + 64 = 0
22. The quadratic equation x² + x + c = 0 has two imaginary solutions. Show that
the constant c must be greater than 1.
Answers
Answer:
Step-by-step explanation:
the degree of a polynomial determines 1:1 the number of solutions.
a quadratic equation (degree 2) has 2 solutions.
the general solution is
x = (-b ± sqrt(b² - 4ac))/(2a)
in our case
a = -4
b = -4
c = -1
so,
x = (4 ± sqrt((-4)² - 4×-4×-1))/(2×-4)
when we look at the square root
16 - 16
we see that it is 0.
the square root of 0 is 0, and there is no difference between -0 and +0.
so, we get only one (real) solution : 4/-8 = -1/2
but : formally, there are still 2 solutions (as this is a quadratic equation). they are just identical.
so, I am not sure what your teacher wants to see in this case as answer.
my answer would be 2 real identical solutions. did this help?
The measures of the angles of △ABC are given by the expressions in the table.

Answers
The angles of the triangle are 125 degrees, 20 degrees, and 35 degrees.
Define triangles.A triangle is a closed geometric shape with three sides, three angles, and three line segments. Three non-collinear points are joined by line segments to create the simplest polygon, which has three non-collinear points.
Triangles can be categorized according to the size of their sides and angles. Triangles can be categorized as equilateral (all sides are equal in length), isosceles (both sides are equal in length), or scalene based on their sides (all sides are different in length). Triangles can be categorized as acute (all angles are less than 90 degrees), obtuse (one angle is greater than 90 degrees), or right (one angle is greater than 90 degrees) (one angle is exactly 90 degrees).
In any triangle, the sum of the three interior angles is always 180 degrees. Therefore, we can write:
a + b + c = 180
Substituting the given values, we get:
(6x-1) + 20 + (x+14) = 180
Simplifying and solving for x, we get:
7x + 33 = 180
7x = 147
x = 21
Now that we have the value of x, we can substitute it back into the expressions for the angles to find their values:
angle a = (6x-1) = (6*21-1) = 125 degrees
angle b = 20 degrees
angle c = (x+14) = (21+14) = 35 degrees
Therefore, the angles of the triangle are 125 degrees, 20 degrees, and 35 degrees.
To know more about triangles, visit:
https://brainly.com/question/17335144
#SPJ1
INDUSTRY Two identical right cylindrical steel drums containing oil need to be covered with a fire-resistant sealant. In order to determine how much sealant to purchase, George must find the surface area of the two drums.
The surface area, including the top and bottom bases, is given by the
formula S = 2πrh + 2πr^2
Answers
Note that the Polynomial Expression for to represent the total surface area of the two drums is: 4πrh + 4hr².
What is a polynomial expression?A polynomial expression is any expression that consists of variables, constants, and exponents and is combined using mathematical operators such as addition, subtraction, multiplication, and division.
According to the number of terms in the expression, polynomial expressions are classed as monomials, binomials, or trinomials.
Given that the total surface area of one cylinder is:
2πrh + 2πr²,
The total surface area of two drums will therefore be:
(2πrh + 2πr²) * 2
⇒ 4πrh + 4hr²
Learn more about Total Surface Areas:
https://brainly.com/question/30135821
#SPJ1

f(x) =x(x-1) on R to R
find A and B such that g: A to B defined by g(x)=f(x) is bijective
this is an algebra question, help.
details are needed
Answers
Answer: To find A and B such that g(x) = f(x) is bijective, we need to ensure that g(x) satisfies the conditions for a bijective function, namely, that it is both injective and surjective.
To show that g(x) is injective, we need to show that for any distinct x1, x2 in A, g(x1) ≠ g(x2). We can do this by assuming that g(x1) = g(x2) and then showing that it leads to a contradiction.
So, let's assume that g(x1) = g(x2). Then, we have:
f(x1) = f(x2)
x1(x1-1) = x2(x2-1)
x1^2 - x1 = x2^2 - x2
x1^2 - x2^2 - x1 + x2 = 0
(x1 - x2)(x1 + x2 - 1) = 0
Since x1 and x2 are distinct, we must have x1 + x2 = 1.
But this is impossible, since x1 and x2 are both real numbers, and the sum of two real numbers cannot equal 1 unless one of them is complex. Therefore, our assumption that g(x1) = g(x2) must be false, and g(x) is injective.
To show that g(x) is surjective, we need to show that for any y in B, there exists at least one x in A such that g(x) = y. In other words, we need to find an expression for x in terms of y.
So, let's solve the equation f(x) = y for x:
x(x-1) = y
x^2 - x - y = 0
Using the quadratic formula, we get:
x = (1 ± √(1 + 4y))/2
Since we want to define g(x) on R, we need to ensure that the expression under the square root is non-negative. This means that 1 + 4y ≥ 0, or y ≥ -1/4.
Therefore, we can define A = [-1/4, ∞) and B = [0, ∞), and g(x) = f(x) is a bijective function from A to B.
A^2 when a=3/4?? Thank you
Answers
Step-by-step explanation:
Given:-\(a = \frac{3}{4} \)
Therefore,
\( {a}^{2} = ( { \frac{3}{4} })^{2} \\ \: \: = \frac{ {3}^{2} }{ {4}^{2} } \\ = \frac{9}{16} \)
Solution:
Given:
\(a = \dfrac{3}{4}\)
Square both sides of the given equation:
\(a = \dfrac{3}{4}\)
\(\rightarrow (a)^{2} = \text{\huge{[}}\dfrac{3}{4}\text{\huge{]}}^{2}\)
Simplify the equation:
\(\rightarrow a^{2} = \text{\huge{[}}\dfrac{3}{4}\text{\huge{]}}\text{\huge{[}}\dfrac{3}{4}\text{\huge{]}}\)
\(\rightarrow a^{2} = \text{\huge{[}}\dfrac{3^{2} }{4^{2} }\text{\huge{]}}\)
\(\rightarrow \boxed{a^{2} =\dfrac{9 }{16 }}\)
A map provided by an engineering firm has a scale of 1 inch to 2000 feet. If the distance from the starting point for a pipeline to the ending point is 13 1/2 inches how long is the pipe line?
Answers
Answer:
27,000 feet
Step-by-step explanation:
Let \(x\) be the actual length of the pipeline, in feet.
Set up the following proportion:
\(\displaystyle\\\frac{1}{2,000}=\frac{13.5}{x}\)
Cross-multiplying yields \(x=13.5\cdot 2,000=\boxed{27,000\text{ ft}}\)
Simplify (3s + 9 - s) + 6(4s - 3^2)
Answers
Answer:
26s - 45
Step-by-step explanation:
I need help with this question

Answers
Where the daily growth factor is 1.15 and the starting height in inches is 7.
What is function?a. Given by, the function that calculates the height of the beanstalk in relation to the time since Gregory planted it.
\(f(t) = 7(1.15)^t\)
where the daily growth factor is 1.15 and the starting height in inches is 7.
B). The following ratios can be calculated using the formula from section (a):
f(1)/f(0) = (71.15¹)/(71.15⁰) = 1.15
f(2)/f(1) = (71.15²)/(71.15¹ = 1.15
f(1)/f(1) = (71.15¹)/(71.15¹) = 1
\(f(9.56)/f(8.56) = (71.15^{9.56})/(71.15^{8.56})\) ≈ 1.15
\(f(8.56)/f(8.55) = (71.15^{8.56})/(71.15^{8.55})\) ≈ 1.15
c. For the any value of z, we have:
\(f(z+1)/f(z) = (71.15^{(z+1)})/(71.15^z)\) = 1.15
and
\(f(z)/f(z-1) = (71.15^z)/(71.15^{(z-1)})\) = 1.15
For question 6:
a. As a increases throughout the function's domain, f(z) [Select an answer]
Since the base of the exponential function is less than 1 (0.69 < 1), as x increases, f(x) will approach 0.
b. The 1-unit growth factor of f is
The 1-unit growth factor for f is 0.69, since f(x+1)/f(x) = 0.69.
c. The -unit growth factor of f is
The 1/2-unit growth factor for f is (0.69)¹/₂, since f(x+1/2)/f(x) = (0.69)¹/₂.
d. The 6-unit growth factor of f is
The 6-unit growth factor for f is (0.69)⁶, since f(x+6)/f(x) = (0.69)⁶.
e. The 6-unit percent change of f is
The 6-unit percent change for f is ((0.69)^6 - 1) * 100%, which is approximately -38.77%.
To know more about growth factor visit:
brainly.com/question/30859558
#SPJ1
The range of the following relation R{(3,-2), (1, 2), (-1, -4), (-1, 2)} is O{-1.1,3) -1,-1,1.3 01-4, 2, 2, 2] {-4, -2, 2
Answers
Answer:
The range is -2,2,-4
Step-by-step explanation:
hope this helps
Please please help!!!!

Answers
Answer:
7 and 1/4
Step-by-step explanation:
Answer:
The answer is 7 1/4 or 29/4
Step-by-step explanation:
Is 2 a solution of 3-p=1