A particle has an initial displacement of s = 0 when t = 0.
The velocity of the particle is v = 6t2 − 60t + 150 m/s (t ≥ 0).
(a) Find the displacement of the particle at time t.
(b) Find the acceleration of the particle at time t.
c) What is the acceleration and displacement when v = 0?
(d) Evaluate (cos(5x) − sin(5x))dx

The series converges for |x| < 1, and the radius of convergence, r, is 1.

To find the radius of convergence, r, of the series ∑ (infinity, n = 0) x^n / (3n − 1), we can use the ratio test. The ratio test states that for a power series ∑ a_n * x^n, if the limit of the absolute value of the ratio of consecutive terms |a_(n+1) / a_n| exists, then the series converges absolutely if the limit is less than 1, and diverges if the limit is greater than 1.

Let's apply the ratio test to our series:

lim (n → ∞) |(x^(n+1) / (3(n+1) - 1)) / (x^n / (3n - 1))|

Simplifying the expression:

lim (n → ∞) |(x^(n+1)(3n - 1)) / (x^n(3(n+1) - 1))|

The x^n terms cancel out:

lim (n → ∞) |(x(3n - 1)) / (3(n+1) - 1)|

Taking the absolute value and simplifying:

lim (n → ∞) |x(3n - 1) / (3n + 2)|

Since we're interested in the radius of convergence, we want to find the value of |x| that makes the limit less than 1. Thus:

|x(3n - 1) / (3n + 2)| < 1

Taking the limit as n approaches infinity, we can ignore the n terms:

|x| < 1

Therefore, the series converges for |x| < 1, and the radius of convergence, r, is 1.

Learn more about converges here:

https://brainly.com/question/31489835

#SPJ11

Answer:

its 3.6

Step-by-step explanation:

Answer:

Step-by-step explanation:

f(x) = x² - 2x + 5

Yo find f(-2) substitute the value of x that's - 2 into f(x) that is for every x in f (x) replace it with - 2

So we have

f( - 2) = (-2)² - 2(-2) + 5

= 4 + 4 + 5

= 8 + 5

We have the final answer as

Hope this helps you

Answer:

(A) \(y = x+3\)

Step-by-step explanation:

Using the values of (-6, -3), (3,6), and (5,8) we can substitute the values into each equation and see if the equation meets the requirements for all 3.

Let's test A first.

\(-3 = -6+3\)

Correct, let's try the second pair.

\(6 = 3+3\)

Correct, let's try the third pair.

\(8 = 5+3\)

So yes, this equation works.

For fun, let's try the other equations.

Let's test B.

\(-3 = -6-3\)

This is not true as -6 -3 = -9. So this equation is immediately ruled out.

Let's test C.

\(-3 = 2\cdot-6\)

Again this doesn't work, as -6 times 2 is -12. So this equation is also ruled out.

Let's try D.

\(-3 = \frac{1}{2}\cdot-6\)

This works, as half of -6 is -3 - however the equation will only work if all 3 pairs work for it.

Let's try the second pair.

\(6 = \frac{1}{2}\cdot3\)

This doesn't work, as half of 3 is 1.5. This equation is also ruled out.

Therefore, A is the only equation that works with these pairs.

Hope this helped!

Given that the expression 15.3 - (23.6 - 25.9) represents A.And, the expression 15.4 - (25.9 - 23.6) represents B.Now, we have to find A - B and plot the value on the top number line. Also, we have to find B - A and plot the value on the bottom number line.

Step 1: Let's first find the value of A15.3 - (23.6 - 25.9) = 15.3 - (-2.3)= 15.3 + 2.3= 17.6So, the value of A is 17.6.Step 2: Let's find the value of B15.4 - (25.9 - 23.6) = 15.4 - 2.3= 13.1So, the value of B is 13.1.

Step 3: Let's find A - B and plot the value on the top number line A - B = 17.6 - 13.1= 4.5On the top number line, mark the point of 4.5.Step 4: Let's find B - A and plot the value on the bottom number line. B - A = 13.1 - 17.6= -4.5On the bottom number line, mark the point of -4.5.Thus, the values of A - B and B - A on the top and bottom number lines are shown below.

To know more about lines visit:

brainly.com/question/2696693

#SPJ11

Answer:

1: square inch

2: both take an amount of space

3: cubic inch

Hope this Helps!

By using the concept of interest, we can calculate the year in which the tuition will reach $10,000 as 2027

Interest is the extra money you pay for borrowing money or for an investment, and it accumulates over time.

In this case, the interest rate is 3%, so the total tuition increases by 3% each year. To calculate the year in which tuition will reach $10,000, we will need to use the following formula:

Interest = (principal × rate × time) / 100.

The principal is $8,000, the rate is 3%, and the time is the number of years it takes for the tuition to reach $10,000. Thus, the equation becomes:

Interest = (8000 × 0.03 × time) / 100.

We can solve for time by multiplying both sides of the equation by 100 and dividing by 240. This gives us the following result:

Time = ($10,000 - $8,000) / (0.03 × $8,000) = 4.17 years.

Therefore, the tuition will reach $10,000 in

(2023 + 4.17) = 2027

To know more about interest here.

https://brainly.com/question/22621039

#SPJ4

Answer:Let's first break apart the problem!

Let x = adult tickets

Let y = child tickets

We know from the problem that a total of 336 tickets were sold.

x + y = 336

We also know from the problem the total profit was $4675. We also know that the adult tickets were $15 per ticket and the child tickets were $10 per ticket.

15x + 10y = 4675

Now we need to combine our two-equation by making a common variable. Let's multiply our first equation by 10 and then combine the two equations.

10x + 10y = 3360

Now lets combine the equations

15x 10y = 4675

-10x - 10y = -3360

to get

5x = 1315

x = 263

Therefore there were 263 adult tickets sold.

Let's set some variables:

Now lets set up the system of equation:

.a + c = 378   --> 14a + 14c = 5292

14a + 6c = 4252

After solving the system of equation, you would get that

a = 248  and  c = 130

That means the theater sold 240 adult tickets and 130 child tickets

Hope that helps!

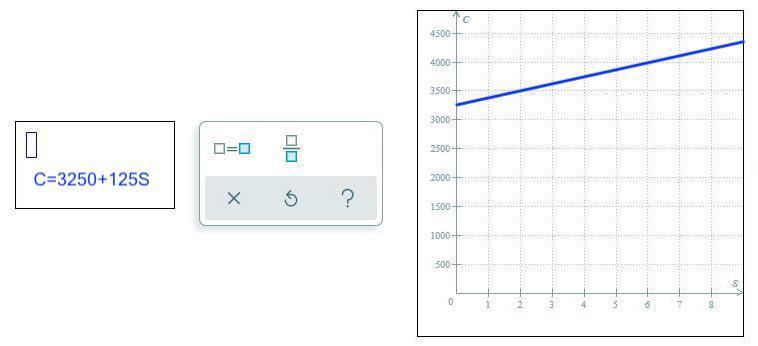
9514 1404 393

Answer:

  see the attachment

Step-by-step explanation:

The cost when no sugar is transported is 3250, so that is the "y-intercept". (There is no "y". The vertical axis is labeled "c", so that  is the c-intercept.)

The cost per ton is 125, so that is the slope or "rate of change". Each increase of 1 unit in the value of "s" will result in an increase of 125 in the value of "c". The grid lines for "c" are 500 apart, so 1 vertical grid space will correspond to 500/125 = 4 horizontal grid spaces.

The graph starts at the left side halfway between 3000 and 3500. It goes up 1 grid square for each 4 grid squares to the right.

The correct match for the graph of the total cost function is the option B graph.

The function is a type of relation, or rule, that maps one input to specific single output.

Given;

y = 2x is function

so, our graph should be of function y = 2x

Here, x is the number of pounds of rice scooped and purchased from a bulk bin at the grocery store and y is the total cost of the rice.

it means x is a number like 0, 1, 2, 3

so, the graph of the total cost function is a discrete function in nature.

Hence, graph-B is correct answer.

Learn more about function here:

https://brainly.com/question/2253924

#SPJ1

One positive angle coterminal with 50° is 410°, and one negative angle coterminal with 50° is -310°.

To find a positive and a negative angle that are coterminal with 50°, we need to add or subtract multiples of 360° from 50°.

Positive angle coterminal with 50°:

To find a positive angle, we can add 360° to 50°:

50° + 360° = 410°

Negative angle coterminal with 50°:

To find a negative angle, we can subtract 360° from 50°:

50° - 360° = -310°

Therefore, one positive angle coterminal with 50° is 410°, and one negative angle coterminal with 50° is -310°.

Learn more angle

brainly.com/question/17039091

#SPJ11

One positive angle and one negative angle that are coterminal with 50° within the interval are 410° and -310° respectively.

To find an angle that is coterminal with 50°, we need to add or subtract a multiple of 360° (one complete revolution) to 50°. We want to find angles that are within the interval, which means we need to find angles between 0° and 360°.

For a positive angle that is coterminal with 50°, we can add 360° until we get an angle between 0° and 360°:

50° + 360° = 410°

So, 410° is a positive angle that is coterminal with 50° within the interval.

For a negative angle that is coterminal with 50°, we can subtract 360° until we get an angle between -360° and 0°:

50° - 360° = -310°

So, -310° is a negative angle that is coterminal with 50° within the interval.

For more questions like Angle click the link below:

https://brainly.com/question/28451077

#SPJ11

Answer:

1. 52*

2. 128* ( I think)

Step-by-step explanation:

Using an linear function, we find that by 2020 only 11% of all American adults believe that most qualified students  get to attend college.

-----------------------------------------

A decaying linear function has the following format:

\(A(t) = A(0) - mt\)

In which

The equation is:

\(A(t) = 45 - 1.7t\)

It will be 11% in t years after 2000, considering t for which A(t) = 11, that is:

\(11 = 45 - 1.7t\)

\(1.7t = 34\)

\(t = \frac{34}{1.7}\)

\(t = 20\)

2000 + 20 = 2020

By 2020 only 11% of all American adults believe that most qualified students  get to attend college.

A similar problem is given at https://brainly.com/question/24282972

The simplified form of the expression is \(\frac{1}{(t+4)^2}\)

Given the expression:

Factorize the denominator as shown:

t^2 + 7t + 12

t^2 + 4t + 3t + 12

t(t+4) + 3(t+4)

(t+4)(t+3)

Substituting into the expression above, we will have:

\(= \dfrac{\frac{t+3}{t+4} }{(t+3)(t+4)}\\=\dfrac{t+3}{t+4} \div (t+3)(t+4)\\=\dfrac{t+3}{t+4} \times \dfrac{1}{(t+3)(t+4)} \\=\dfrac{1}{(t+4)^2}\)

Hence the simplified form of the expression is \(\frac{1}{(t+4)^2}\)

Learn more on indices here: https://brainly.com/question/15361818

Answer:

3rd option

Step-by-step explanation:

Answer:

60°

Step-by-step explanation:

180-120 = 60

The reason is a straight line is 180 degrees and we have 120 degrees and just need to find x.

Answer:

Step-by-step explanation:

-3x + y = 22     ⇒  y = 3x + 22

-12x - 10y = -10  and  y = 3x + 22

-12x - 10(3x + 22) = -10

-12x - 30x - 220 = -10

               +220       +220

 - 42x  = 210  

 ÷(-42)     ÷(-42)

    x = -5

y = 3(-5) + 22 = -15 + 22 = 7

To find the radius of convergence, R, of the series

Σ (n!)^(k+4)/((k+4)n)! x^n

we can use the ratio test. The ratio test states that if

lim |a_(n+1)/a_n| = L as n approaches infinity,

then the series converges if L < 1 and diverges if L > 1.

Applying the ratio test to our series, we have:

|((n+1)!)^(k+4)/((k+4)(n+1))! x^(n+1)| / |(n!)^(k+4)/((k+4)n)! x^n|

Simplifying this expression, we get:

|n+1| |x| / (k+4)(n+1)

As n approaches infinity, the term |n+1| / (n+1) simplifies to 1, and the expression becomes:

|x| / (k+4)

For the series to converge, we need |x| / (k+4) < 1. This implies that the radius of convergence, R, is given by:

R = k + 4

Therefore, the radius of convergence, R, for the given series is k + 4.

Learn more about convergence here: brainly.com/question/32234460

#SPJ11

Answer: 3.5

Step-by-step explanation:

The number of color sequences possible when removing five balls one at a time depends on the number of different colors the balls have.

If there are C different colors, the number of color sequences possible is C^5 (C raised to the power of 5), since for each ball you remove, you have C options for its color.

The number of combinations of colors possible when removing five balls one at a time is given by the binomial coefficient "C choose 5", which represents the number of ways to choose 5 balls out of C different balls, ignoring the order in which they are chosen.

The binomial coefficient can be calculated as:

C choose 5 = C! / (5! * (C-5)!).

Here, "!" denotes the factorial symbol, which is the product of all positive integers up to that number (e.g. 5! = 5 * 4 * 3 * 2 * 1 = 120).

To know more about Permutation:

https://brainly.com/question/1216161

#SPJ4

Answer:

5^(3) is the exponent form which equals 125desks

Step-by-step explanation:

A row has 5 desks

A classroom has 5 rows of desks= 5*5 desks

The school has 5 classrooms

=5*5+5*5+5*5+5*5+5*5 desks

=5^(2)+5^(2)+5^(2)+5^(2)+5^(2)

=5[5^(2)]

=5^(3) = 125 desks

1/28561 is the probability that all four cards are kings

Hearts, clubs, spades, and diamonds make up the four suites of a normal deck of cards. thirteen cards total—aces, 2, 3, 4, 5, 6, 7, 8, 9, 10, jack, queen, and king—make up each suite. Thus, there are 52 cards in all in the deck.

The four French suits—clubs, diamonds, hearts, and spades—each have 13 ranks. King, Queen, and Jack are the three court cards (face cards) in each suit, and their pictures are reversed (double-headed). The ten numerical cards, or pip cards, in each suit range in value from one to 10.

In a pack of cards, there are 52 cards and 4 Kings.

Probability of picking a King is:  4/52 = 1/13 .

Since a card is being replaced before picking up the next card, the probability of picking a King is always  1/13 .

Picking a subsequent King is independent of picking a King previously and thus we multiply the individual probabilities to arrive at the combined probability.

Thus, the required probability is:

= 1/13 × 1/13 × 1/13 × 1/13

= 1/28561

To know more about probability refer to:

https://brainly.com/question/13604758

#SPJ4

The probability of the interval -1.62 < z < 2.01 in a standard normal distribution is approximately 0.9262 or 92.62%.

In a standard normal distribution, the mean is 0 and the standard deviation is 1. The z-score represents the number of standard deviations a data point is from the mean. To find the probability of a specific interval, we calculate the area under the curve between the corresponding z-values.

Given the interval -1.62 < z < 2.01, we need to find the area under the standard normal curve between these two z-values. This can be done using a standard normal distribution table or by using a statistical software or calculator.

By looking up the z-values in the table or using software, we find the corresponding probabilities: P(z < -1.62) = 0.0526 and P(z < 2.01) = 0.9788.

To find the probability of the interval -1.62 < z < 2.01, we subtract the probability of the lower bound from the probability of the upper bound: P(-1.62 < z < 2.01) = P(z < 2.01) - P(z < -1.62 = 0.9788 - 0.0526 = 0.9262.

Learn more about normal distribution here:

https://brainly.com/question/15103234

#SPJ11

Answer:

Let P(h,k) be the point which is equidistant from the point (2,4) and the y-axis. The distance of point P(h,k) from the y-axis is h. ∴h=√(h−2)2+(k−4)2⇒h2−4h−4+k2−8k+16=h2⇒k2−4h−8k+20=0.

Hence,the locus of (h,k)is y2−4x−8y+20=0.

Step-by-step explanation:

Answer:

1/2 ㏑(sec (2x + 9)) + c  ........ absolute sec (2x +9)

Step-by-step explanation:

∫tan (2x + 9) dx

let u = 2x + 9

du/dx = 2

dx = du/2 = (1/2) du

now we have ∫tan u (1/2  du)

= 1/2 ∫tan u du

= 1/2 ㏑ (sec u) ...... absolute

=1/2 ㏑(sec (2x + 9)) + c ........ absolute

Answer:

y = -4x + 58

Step-by-step explanation:

Equation of line: y =mx + b

  Here, m is the slope and b is the y-intercept.

Parallel lines have same slope.

      y = -4x + 9

 m = -4

Equation of the required line: y = -4x + b

The line passes through (15, -2). Substitute x and y values and find the value of 'b'.

       -2 = -4*15 + b

        -2 = -60 + b

-2 + 60 = b

      b = 58

Equation of line:

        y = -4x + 58

Answer: B. 1 3/8 One and three-eighths

Step-by-step explanation:

Answer:

i think is b

Step-by-step explanation:

The results of the operations between two complex numbers are listed below:

Case A: z + w = 2√6 + i 2√6, z - w = - 2√2 + i 2√2

Case B: z + w = √2 / 2 - i √2 / 2, z - w = - √6 / 2 - i √6 / 2

In this problem we find two complex numbers, whose following operations must be found: addition, subtraction. These operations are perform by component addition:

Case A

z + w = (4 · cos 75° + i 4 sin 75°) + (4 · cos 15° + i 4 · sin 15°)

z + w = 2√6 + i 2√6

z - w = (4 · cos 75° + i 4 sin 75°) - (4 · cos 15° + i 4 · sin 15°)

z - w = - 2√2 + i 2√2

Case B

z + w = (cos 255° + i sin 255°) + (cos 15° + i sin 15°)

z + w = √2 / 2 - i √2 / 2

z - w = (cos 255° + i sin 255°) - (cos 15° + i sin 15°)

z - w = - √6 / 2 - i √6 / 2

To learn more on complex numbers: https://brainly.com/question/18392150

#SPJ1