.A major traffic problem in the Greater Cincinnati area involves traffic attempting to cross the Ohio River from Cincinnati to Kentucky using Interstate 75. Let us assume that the probability of no traffic delay in one period, given no traffic delay in the preceding period, is 0.85 and that the probability of finding a traffic delay in one period, given a delay in the preceding period, is 0.75. Traffic is classified as having either a delay or a no-delay state, and the period considered is 30 minutes. a. Assume that you are a motorist entering the traffic system and receive radio report of a traffic delay. What is the probability that for the next 60 minutes (two time periods) the system will be in the delay state? Note that this result is the probability of being in the delay state for two consecutive periods. If required, round your answer to three decimal places. b. What is the probability that in the long run the traffic will not be in the delay state? If required, round your answers to three decimal places. C. An important assumption of the Markov process model presented here has been the constant or stationary transition probabilities as the system operates in the future. Do you believe this assumption should be questioned for this traffic problem? Explain. The input in the box below will not be graded, but may be reviewed and considered by your instructor.
Answers
a) The probability of the traffic system being in the delay state for the next 60 minutes is 0.5625.
b) The probability that the traffic will not be in the delay state in the long run is approximately 0.375. The assumption of constant transition probabilities in the Markov process model for this traffic problem may be questionable due to the dynamic nature of traffic conditions and external factors.
a. To find the probability that the system will be in the delay state for the next 60 minutes (two time periods), we can use the given transition probabilities.
Let D represent the delay state and N represent the no-delay state.
We are given that the probability of a delay in one period, given a delay in the preceding period, is 0.75. Therefore, P(D|D) = 0.75.
To find the probability of being in the delay state for two consecutive periods, we multiply the conditional probabilities:
P(D, D) = P(D|D) * P(D|D) = 0.75 * 0.75 = 0.5625.
So, the probability of the system being in the delay state for the next 60 minutes is 0.5625.
b. To find the probability that in the long run the traffic will not be in the delay state, we need to find the steady-state probabilities of the system. Let's denote P(D) as the probability of being in the delay state and P(N) as the probability of being in the no-delay state in the long run.
We can set up the following equations based on the given transition probabilities:
P(D) = 0.85 * P(N) + 0.75 * P(D)
P(N) = 0.15 * P(N) + 0.25 * P(D)
Solving these equations, we can find the steady-state probabilities. The steady-state probability of not being in the delay state is P(N).
Using the equations above, we can find P(N) = 0.15 / (0.15 + 0.25) ≈ 0.375.
Therefore, the probability that in the long run the traffic will not be in the delay state is approximately 0.375.
c. The assumption of constant or stationary transition probabilities may be questionable for this traffic problem. Traffic conditions can vary significantly over time, affected by factors such as rush hours, accidents, construction, and other unpredictable events. The Markov process model assumes that the transition probabilities remain constant, but in reality, they may change depending on various factors. Therefore, it is important to consider the dynamic nature of traffic patterns and external factors that can impact traffic delays when applying the Markov process model to this traffic problem.
To learn more about Markov process click here: brainly.com/question/15057441
#SPJ11
Related Questions
On Friday, the ratio of hamburger orders to hot dog orders in the school cafeteria was 15:10. Simplify the ratio into simpliest terms. (Divide both parts by the GCF)
Answers
The ratio of harmburger order to hot dog orders in the school cafeteria is 15:10. The ratio can be simplified below
we have to divide both ratio by the greatest common factor. The greatest common factor of the ratio 15 and 10 is 5. Therefore,
\(\begin{gathered} 15\colon10 \\ \frac{15}{10}\text{ }\div\frac{5}{5}=\frac{3}{2} \\ 3\colon2 \end{gathered}\)The ratio to the lowest term is 3:2
In a survey, 20 people were asked how much they spent on their child's last birthday gift. The results were roughly bell-shaped with a mean of $44 and standard deviation of $10. Estimate how much a typical parent would spend on their child's birthday gift (use a 99% confidence level). Give your answers to one decimal place. Provide the point estimate and margin or err
Answers
Based on the survey results, a typical parent would spend around $44 on their child's birthday gift, with a margin of error of approximately $2.9 at a 99% confidence level.
To estimate how much a typical parent would spend on their child's birthday gift, we use the sample mean and standard deviation as estimates of the population parameters. The sample mean of $44 serves as the point estimate for the population mean.
To determine the margin of error, we use the standard error, which is the standard deviation divided by the square root of the sample size. In this case, the standard error is approximately $2.5 (standard deviation of $10 divided by the square root of 20). Multiplying the standard error by the critical value corresponding to a 99% confidence level (z-value of 2.58 for a large sample size) gives us the margin of error.
Therefore, the typical amount spent on a child's birthday gift is estimated to be $44, with a margin of error of approximately $2.9. This means that we can be 99% confident that the true mean amount spent by parents falls within the range of $41.1 to $46.9.
Learn more about standard error here:
https://brainly.com/question/13179711
#SPJ11
the average score for morning students was 76 and the average score for afternoon students was 80. the professor concludes that the afternoon is the best time for students to complete the exam and that the difference in average scores reveals an important difference between afternoon and morning classes in college. describe how sampling error could account for this difference. the difference between means could be due to .
Answers
Sampling error could account for the difference in average scores between morning and afternoon students because the sample of students who took the exam in the morning may not be representative of all morning students, and the sample of students who took the exam in the afternoon may not be representative of all afternoon students.
This means that the difference in average scores could be due to chance rather than a real difference between morning and afternoon classes. Additionally, other factors such as the students' prior knowledge, preparation and motivation might also have a role in the difference in average scores.
Sampling error in exam scoresSampling error occurs when a sample of data is not representative of the population from which it is drawn. This can happen for a variety of reasons, such as the sample being too small, or the sample being selected in a biased way.
In the case of the morning and afternoon students, if the sample of students who took the exam in the morning is not representative of all morning students, it could mean that the average score for the sample is not the same as the average score for the population of all morning students. Similarly, if the sample of students who took the exam in the afternoon is not representative of all afternoon students, the average score for the sample may not be the same as the average score for the population of all afternoon students.
Learn more about Sampling error in exam scores here:
https://brainly.com/question/12004009
#SPJ4
Find the simplified product: 2 square root of 5x^3(-3 square root of 10x^2)

Answers
Answer:
Step-by-step explanation:
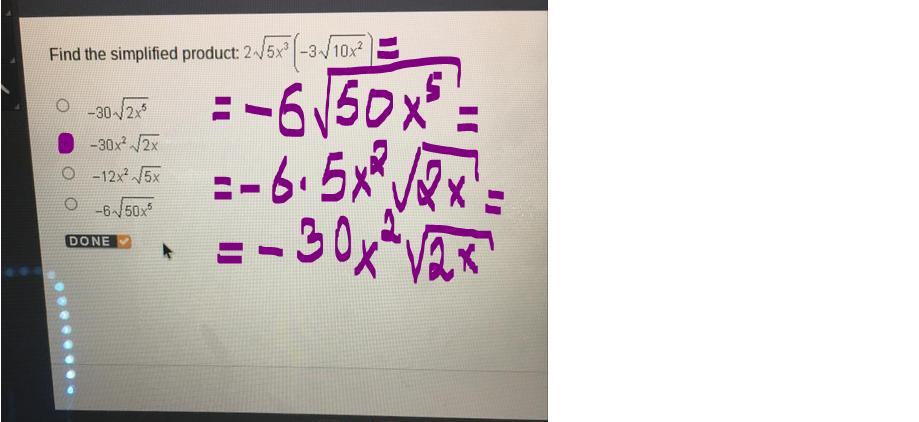
10 cm 10 cm 8 cm 6cm Find the area of trapezoid ABCD.
Answers
Answer:
need more context
Step-by-step explanation:
Trapezoid area formula:
A=(base¹+base²/2)×height
Please help me with hw

Answers
Answer:
4. 7 hours 6. 8.57
Step-by-step explanation:
Step-by-step explanation:
Since, Carlos completes the work in 5 hours.
So, in one hour she will do \( =\frac{1}{5}\) part
Since, Jenny completes the work in 9 hours.
So, in one hour she will do \( =\frac{1}{9}\) part
(Carlos + Jenny)'s one hour work together
\( =\frac{1}{5}+\frac{1}{9}\\
= \frac{9+5}{5\times 9}\\
= \frac{14}{45}\\\)
Total time taken by Carlos and Jenny together \( =\frac{45}{14}= 3\frac{3}{14} \: hours\)
Can someone help me thank you

Answers
The value of the fractions will be:
1. 4/10 + 2/10 = 6/10
2. 9 /12 + 3/12 = 1
3. 6/10 + 4/10 = 1
4. 2/8 + 3/8 = 5/8
5. 2/7 + 6/7 = 1 1/7
6. 11/9 + 8/9 = 2 1/9
7. 5/13 + 10/13 = 1 2/13
8. 3/5 + 7/10 = 1 3/10
9. 7/8 + 13/16 = 1 11/16
10. 9/30 + 3/5 = 9/10
How to calculate the fractionA fraction simply means a piece of a whole. In this situation, the number is represented as a quotient such that the numerator and denominator are split. In this situation, in a simple fraction, the numerator as well as the denominator are both integers.
It should be noted that in order to add the numbers it's essential to have a common denominator. For example, 7/8 + 13/16 will be:
= 7/8 + 13/16
= 14/16 + 13/16
= 27/16
= 1 11/16
Learn more about fractions on:
brainly.com/question/78672
#SPJ1
33–36 find an equation of the tangent line to the curve at the given point. 33. y − 2x 3 2 x 2 1 2, s1, 3d
Answers
The derivative of y = 2x^3 - 2x^2 + 1/2 is dy/dx = 6x^2 - 4x. Substituting x = 1, the slope is 2. Using the point-slope form with (1, 3), the equation of the tangent line is y = 2x + 1.
To find the equation of the tangent line to the curve at the given point, we first need to find the derivative of the curve.
The given curve is:
y = 2x^3 - 2x^2 + 1/2
To find the derivative, we differentiate each term with respect to x:
dy/dx = d/dx (2x^3) - d/dx (2x^2) + d/dx (1/2)
= 6x^2 - 4x
Now, let's find the slope of the tangent line at the point (1, 3). We substitute x = 1 into the derivative:
m = dy/dx |x=1
= 6(1)^2 - 4(1)
= 6 - 4
= 2
So, the slope of the tangent line at the point (1, 3) is 2.
Next, we use the point-slope form of a linear equation to find the equation of the tangent line:
y - y1 = m(x - x1)
Substituting the values (x1, y1) = (1, 3) and m = 2, we get:
y - 3 = 2(x - 1)
Expanding and rearranging:
y - 3 = 2x - 2
y = 2x + 1
Therefore, the equation of the tangent line to the curve y = 2x^3 - 2x^2 + 1/2 at the point (1, 3) is y = 2x + 1.
To learn more about tangent line click here brainly.com/question/31617205
#SPJ11
The sum of the digits of a positive 2-digit number is 12. The units digit is 3 times the tens digit. Find the number
Answers
The sum of the digits is 12:
x + y = 12
The units digit is 3 times the tens digit:
y = 3x
To find the number, we need to find the values of x and y that satisfy both equations simultaneously.
From equation (2), we can substitute the value of y in equation (1):
x + 3x = 12
4x = 12
x = 3
Substituting the value of x back into equation (2):
y = 3 * 3
y = 9
Therefore, the number is 39.
A pharmacist mixes 10 grams of a 15% medicine solution with 25 grams of a 10% medicine solution. Suppose we know that after she adds the x grams of pure medicine the pharmacists mixture is 25% medicine solution. Write an equation
Answers
The equation that represents the situation is (4 + x) / (10 + 25 + x) = 0.25
Let's start by finding the amount of medicine in the original mixture before adding any pure medicine.
The amount of medicine in the 10 grams of 15% solution is
0.15 × 10 = 1.5 grams
The amount of medicine in the 25 grams of 10% solution is
0.10 × 25 = 2.5 grams
So the total amount of medicine in the original mixture is,
1.5 + 2.5 = 4 grams
Now let x be the amount of pure medicine added.
The total amount of medicine in the final mixture is,
4 + x
The total amount of solution in the final mixture is,
10 + 25 + x
So the concentration of the final mixture is,
(4 + x) / (10 + 25 + x)
We know that this concentration is 25%, so we can write:
(4 + x) / (10 + 25 + x) = 0.25
This is the equation that represents the situation.
Learn more about equation here
brainly.com/question/14603452
#SPJ4
The given question is incomplete, the complete question is:
A pharmacist mixes 10 grams of a 15% medicine solution with 25 grams of a 10% medicine solution. Suppose we know that after she adds the x grams of pure medicine the pharmacists mixture is 25% medicine solution. Write an equation that represents the situation
find the value of b if the following figures are similar.

Answers
Answer:
7
Step-by-step explanation:
20 - 12 = 8
15 - b = 8
-b = 8 - 15
b = 7 ( -ve signs will become +ve)
b = 15 - 8
b = 7
Cylinder A has a radius of 6 feet and a height that is 5.5 feet less than Cylinder B. Cylinder b has a radius of 4. The cylinders have the same surface area. Find the height of each cylinder.
Answers
Considering the equation for the surface area of a cylinder, we have that the heights are given as follows:
Cylinder A: 1 feet.Cylinder B: 6.5 feet.What is the surface area of a cylinder?The surface area of a cylinder of radius r and height h is given by the following equation:
S = 2πr(r + h).
In this problem, we have that:
Cylinder A has radius r = 6 and height h = h - 5.5.Cylinder B has radius r = 4 and height h.They have the same surface areas, hence:
12π(6 + h - 5.5) = 8π(4 + h)
12(0.5 + h) = 32 + 8h
6 + 12h = 32 + 8h
4h = 26
h = 6.5.
Hence the heights are given as follows:
Cylinder A: 1 feet.Cylinder B: 6.5 feet.More can be learned about the surface area of a cylinder at https://brainly.com/question/26702574
#SPJ1
Accurately construct triangle ABC using the information below
AB=8cm
AC=5cm
Angle BAC=70 degrees
Answers
Connect the points where the first arc crosses the triangle's base and the second arc intersects the base of the triangle with the straightedge to create the triangle's third side, BC.
What is triangle ABC?Generally, To accurately construct triangle ABC, you will need a straightedge (such as a ruler) and a protractor. Here are the steps to follow:
Use the straightedge to draw a straight line segment of length 8 cm, which will represent side AB. This line segment will be the base of the triangle.
Place the point of the protractor at one end of the line segment and draw an arc that intersects the other end of the line segment.
Measure the angle formed by the line segment and the arc using the protractor. The measure of this angle should be 70 degrees.
Without changing the position of the protractor, draw another arc that intersects the first arc and the base of the triangle.
Use the straightedge to connect the point where the second arc intersects the base of the triangle to the point where the first arc intersects the base of the triangle. This will form the third side of the triangle, AC.
Finally, use the straightedge to draw the third side of the triangle, BC, by connecting the point where the first arc intersects the base of the triangle to the point where the second arc intersects the base of the triangle.
Read more about triangle
https://brainly.com/question/29285631
#SPJ1
WILL MARK BRAINLIEST!!

Answers
Answer:
area of hexagon = 600√3 m²
explanation:
apothem² = 20² - 10² = 400 - 100 = 300
apothem of hexagon = √300 = 10√3 m²
area of hexagon = 1/2(6 x 20)(10√3) = 600√3 m²
Answer:
Step-by-step explanation:
One way to find the area of the hexagon is to use the formula \(A=\frac{1}{2}ap\), where p is the perimeter and a is the apothem (distance from the center to the midpoint of one side).
The problem says the side length is 20, so the perimeter is 6 x 20 = 120.
The apothem is the distance marked by the dotted line. The rectangles height is \(20\sqrt{3}\), so the apothem is half of that, \(10\sqrt{3}\).
The area is \(\frac{1}{2}\cdot 10\sqrt{3} \cdot 120=600\sqrt{3}\)
suppose the reading rate of 6th grade students is uniformly distributed (this phrase tells you to use the uniform distribution!) between 100 and 180 words per minute. calculate probability that a selected student has a reading rate less than 115 words per minute.
Answers
Answer:
0.84 or 0.48 I cant remember
Step-by-step explanation:
my picture of good luck

PLEASE HELP!!!!!!! What is the slope of the line?
−53
−35
35
53

Answers
Answer:
Slope = 1
Step-by-step explanation:
How do you find the area of a triangle? Is it base x height divided by 2???
Answers
Answer:
yes The area of a triangle is b x h / 2 (base times height divided by 2)
Hi there!
»»————- ★ ————-««
I believe your answer is:
\(\boxed{\frac{b*h}{2}}\)
You should be correct.
»»————- ★ ————-««
Here’s why:
The given formula for a triangle is similar to the formula for area of a square or rectangle. A triangle is basically a 'half-rectangle'.⸻⸻⸻⸻
\(\boxed{\text{Area of a triangle:}}\\\\A = \frac{b*h}{2}\\\\\boxed{\text{Key:}}\\\\\rightarrow \text{B - Base}\\\\\rightarrow \text{H - Height}\)
⸻⸻⸻⸻
The area of a triangle is the half the product of the base and height of the triangle.⸻⸻⸻⸻
»»————- ★ ————-««
Hope this helps you. I apologize if it’s incorrect.
Jubal wrote the four equations below. He examined them, without solving them, to determine which equation has no solution. 7 x + 1 = 7 x+ 1. 3 x + 2 = 3 x minus 2. 4 x + 1 = 3 x + 8. Negative 2 x minus 1 = negative 2 x minus 1. Which of Jubal's equations has no solution? 7 x + 1 = 7 x+ 1 3 x + 2 = 3 x minus 2 4 x + 1 = 3 x + 8 negative 2 x minus 1 = negative 2 x minus 1
Answers
Given:
Four equations are
\( 7 x + 1 = 7 x+ 1\)
\(3 x + 2 = 3 x-2\)
\(4 x + 1 = 3 x + 8\)
\(-2x-1 = -2 x-1\)
To find:
Without solving which equation has no solution.
Solution:
We know that, in an equation
1. No solution : When variable terms are same but constants are different.
2. Unique solution : When variable terms are different.
3. infinitely many solution : When variable terms and constants are same.
In first and fourth equations, terms on left sides are equal to the terms on the right side. So, LHS = RHS for any value of x.
Therefore, these two equations (first and fourth) have infinitely many solutions.
In second equation, variable terms are same on both sides, but the constants are difference. So, LHS ≠ RHS for any value of x.
Therefore, the second has no solutions.
In third equation, coefficient of x are difference on both sides.
So, this equation has unique solution.
Therefore, Jubal's equations \(3 x + 2 = 3 x-2\) has no solution. Hence, the correct option is B.
Answer:
D
Step-by-step explanation:
A ladder 7.00 m long feans against the side of a building. If the fadder is indined at an angle of 76.0
∘
to the harzontal, what is the horizontal distance from the bottom of the ladder to the building (in m )? m
Answers
To find the horizontal distance from the bottom of the ladder to the building, we can use trigonometry and the given information.
The ladder forms a right triangle with the ground and the side of the building. The length of the ladder, 7.00 m, represents the hypotenuse of the triangle. The angle between the ladder and the horizontal ground is given as 76.0 degrees.
To determine the horizontal distance, we need to find the adjacent side of the triangle, which corresponds to the distance from the bottom of the ladder to the building.
Using trigonometric functions, we can use the cosine of the angle to find the adjacent side. So, the horizontal distance can be calculated as follows:
Horizontal distance = Hypotenuse (ladder length) * Cos(angle)
Substituting the values, we have:
Horizontal distance = 7.00 m * Cos(76.0 degrees)
Evaluating this expression, the horizontal distance from the bottom of the ladder to the building is approximately 1.49 m.
To know more about trigonometry click here: https:/brainly.com/question/11016599
#SPJ11
Three straight roads join three towns, A, B and C. The road between towns A and C, 45 km long,
makes an angle of 70° with the road between towns A and B, and the angle of 60° with the road betweer
towns and B. A person drives from A to B to C. Determine the total distance driven.
Answers
We can say for certain that the minimum distance driven would be 45 km (if the person drove directly from A to C without passing through B), and the maximum distance driven would be 90 km (if the person took the longest possible routes from A to B and from B to C).
Based on the information provided, we can visualize a triangle with each town located at a vertex and the roads representing the sides. Town A is connected to town C by a road that is 45 km long, so we can assume that the other two sides (connecting A to B and B to C) have unknown lengths.
Now, let's consider the person's journey from town A to town B to town C. They will have to drive along two sides of the triangle, namely from A to B and from B to C. To determine the total distance driven, we simply need to add up the lengths of these two sides.
Unfortunately, we don't have enough information to calculate the exact lengths of these sides. However, we can make an educated guess based on the triangle inequality theorem, which states that the sum of any two sides of a triangle must be greater than the third side. In other words, if we know two sides of a triangle, we can determine a range of possible lengths for the third side.
In this case, we know that the road between A and C is 45 km long. Let's say that the road between A and B is x km long and the road between B and C is y km long. According to the triangle inequality theorem, we have the following inequalities:
x + y > 45 (since the road between A and B plus the road between B and C must be greater than the road between A and C)
x + 45 > y (since the road between A and B plus the road between A and C must be greater than the road between B and C)
y + 45 > x (since the road between B and C plus the road between A and C must be greater than the road between A and B)
We can simplify these inequalities by subtracting 45 from each side:
x + y - 45 > 0
x - y < 45
y - x < 45
Now we have a system of three inequalities that describe the possible values of x and y. We can graph these inequalities on a coordinate plane (with x representing the distance from A to B and y representing the distance from B to C) to see the region of possible solutions.
Unfortunately, I'm not able to include a graph in my answer since this platform only supports text. However, I can describe the region of possible solutions. It turns out that the region is a triangular shape with vertices at (0, 0), (45, 0), and (22.5, 22.5). This means that the distance from A to B could be anywhere from 0 to 45 km, and the distance from B to C could be anywhere from 0 to 45 km, as long as the sum of these distances is greater than 45 km.
So, to determine the total distance driven by the person, we need to consider all the possible combinations of x and y that satisfy the given conditions and add up their lengths. This would be a tedious calculation to do by hand, so I'll leave it at that. However, we can say for certain that the minimum distance driven would be 45 km (if the person drove directly from A to C without passing through B), and the maximum distance driven would be 90 km (if the person took the longest possible routes from A to B and from B to C).
Learn more about Distance here: brainly.com/question/29288405
#SPJ11
how many ways are there to put 5 balls in 2 boxes if the balls are distinguishable but the boxes are not?
Answers
There are 10 ways to put 5 balls in 2 boxes
A Combination formula C(n , r) = \(\frac{n!}{r! (n -r)!}\) is used when
We wish to find the total number of ways of distributing objects that are not distinguishable Given that, a total set of objects is nDistributed in r other objectsGiven that, the total balls are 5:
n=5
We have wished to distribute them in 2 boxes:
r=2
Since the objects are indistinguishable, we can be used the combinations formula:
C(n , r) = \(\frac{5!}{2! 3!} = 10\)
Hence, there are 10 ways to put 5 balls in 2 boxes.
Read more about the combination:
https://brainly.com/question/28065038
#SPJ4
a survey organization polls 500 registered voters and one of the pieces of information they collect is the voters' incomes. the average income in the sample is $65,000 per year and the sd is $35,000. the histogram of the sampled incomes is skewed to the right, and 110 (22%) of the sampled voters saying they have an income of $150,000 or more. calculate a 95%-confidence interval for the percentage of all voters in the population who have an income of $150,000 or more. group of answer choices
Answers
The 95% confidence interval for the percentage of all voters in the population who have an income of $150,000 or more is approximately (18.38%, 25.62%).
To calculate the 95% confidence interval for the percentage of all voters in the population who have an income of $150,000 or more, we can use the following formula:
CI = p ± z*sqrt((p*(1-p))/n)
Where:
p = proportion of voters in the sample who have an income of $150,000 or more = 110/500 = 0.22
z* = z-score corresponding to 95% confidence level = 1.96 (from standard normal distribution)
n = sample size = 500
Plugging in these values, we get:
CI = 0.22 ± 1.96*sqrt((0.22*(1-0.22))/500)
CI = 0.22 ± 0.049
CI = (0.171, 0.269)
Therefore, we can be 95% confident that the percentage of all voters in the population who have an income of $150,000 or more is between 17.1% and 26.9%.
To calculate a 95% confidence interval for the percentage of all voters in the population who have an income of $150,000 or more, we will use the following formula:
CI = p-hat ± Z * √(p-hat * (1 - p-hat) / n)
Where:
- CI represents the confidence interval
- p-hat is the sample proportion (110/500 = 0.22)
- Z is the Z-score for a 95% confidence interval (1.96)
- n is the sample size (500)
Plugging the values into the formula:
CI = 0.22 ± 1.96 * √(0.22 * (1 - 0.22) / 500)
CI = 0.22 ± 1.96 * √(0.1716 / 500)
CI = 0.22 ± 1.96 * 0.01845
CI = 0.22 ± 0.03612
Learn more about population here
https://brainly.com/question/25630111
#SPJ11
Georgie borrows £12000 for a luxury cruise
The simple interest rate is 7.5% p.a.
Calculate her monthly repayment
if she takes the loan for 3 years.
Answers
Answer:
$14,700
Step-by-step explanation:
interest rate is $900 per year (12000×.075)
$900 × 3 years = $2,700
add $2,700 to $12,000 (amount borrowed)
total is $14,700
Could you help me understand how to find equivalent equations like this

Answers
For the given equation, we will find the value of (a) to find the equivalent equations.
First equation:
\(\begin{gathered} 3a+6=15 \\ 3a=15-6 \\ 3a=9 \\ a=\frac{9}{3}=3 \end{gathered}\)Second equation:
\(\begin{gathered} 3a=9 \\ a=\frac{9}{3}=3 \end{gathered}\)Third equation:
\(\begin{gathered} a+2=5 \\ a=5-2 \\ a=3 \end{gathered}\)Fourth equation:
\(\begin{gathered} \frac{1}{3}a=1\rightarrow(\times3) \\ 3\cdot\frac{1}{3}a=3\cdot1 \\ \\ a=3 \end{gathered}\)As shown all the equations given the same value of a = 3
So, the answer will be Y
Can a triangle be classified as both isosceles AND obtuse? Why or why not?
Answers
Think of a number. Double the number. Add 200. Divide the answer by 4. Subtract one-half the original number. What is the value of the result?
Answers
Answer:
50
Step-by-step explanation:
When a random representative sample is drawn from a population, the procedure is deemed to be what type of sample?
Answers
The procedure which is deemed to be the type of sample in discuss is; representative sample are free of bias.
What is a random sampling?Representative sampling and random sampling are two techniques used to help ensure data is free of bias. A representative sample on the other hand is a group or set chosen from a larger statistical population according to specified characteristics. A random sample is a group or set chosen in a random manner from a larger population.
Read more on representative sampling;
https://brainly.com/question/25142707
#SPJ4
sindi covers 72 km in 6 hours and 15 minutes on her racing bike calculate her average speed
Answers
Answer: 11.25 kmph or 6.99 mph
Step-by-step explanation:
take the speed equation s=d/t (speed equals distance over time)
s=72/6.4 (15 min is 0.4 of an hour)
your final answer will be S= 11.25 kilometers per hour or 6.99 miles per hour
Circle any part of this problem where you see a mistake (there is at least one) then explain why it was a mistake in the textbox and type in the correct answer.

Answers
Answer:
Circle the -3 or the -2 in the final product
Step-by-step explanation:
If you multiply it out, the last terms are -2 and -3 which equal 6, not negative 6 so, that would be wrong factoring.
Multiply polynomials. 1) −3x-³y²z(4x5yz − 2x³y−²z4) Simplify. Write your answer using only positive exponents. 3 2) 36a5b 24a-²b7 3) Factor expression completely. x³ 3x² 25x + 75 Multiply/Divide the rational expressions x²-12x+35 4) 3x+21 X x²-49 2x²-10x 48g5 5) 12x²y7 18zw² 54z6w6 Add or subtract rational expressions, reduce if possible. 7x-5 5x-13 2x-3 2x-3 Solve Linear Equation: 7 7) 1/1×- ² = 5*- 1 8 15 x ——=— x+ 10 6 15 30 + ÷
Answers
(1.) By multiplying the polynomials −3x⁻³y²z and (4x⁵yz − 2x³y⁻²z⁴) simplified expression is -12x²y³z + 6z⁴.
(2.) By multiplying the polynomials 36a⁵b and 24a⁻²b⁷ simplified expression is 864a³b⁸.
(3.) By factoring the expression x³ + 3x² + 25x + 75 simplified expression is (x + 3)(x² + 25).
(4.) By multiplying the rational expressions (3x + 21) and (x² - 49) we get the expression as 3x³ + 21x² - 147x - 1029.
(5.) By multiplying the rational expressions (12x²y⁷) / (18zw²) * (54z⁶w⁶) we get the expression as 12x²y⁷z⁵w³.
(6) By adding or subtracting the rational expressions, (7x - 5) / (5x - 13) - (2x - 3) / (2x - 3) we get the expression as (5x - 2) / (5x - 13).
(7.) By cross-multiplication the equation 1/(1-x²) = 5/(x - 1) we get expression as 5x² - 2x - 6 = 0.
(1.) To multiply the polynomials −3x⁻³y²z and (4x⁵yz − 2x³y⁻²z⁴), we can use the distributive property.
−3x⁻³y²z(4x⁵yz − 2x³y⁻²z⁴) = −3x⁻³y²z(4x⁵yz) + (-3x⁻³y²z)(-2x³y⁻²z⁴)
Applying the distributive property, we multiply each term individually:
= (-3)(4)(x⁻³)(x⁵)(y²)(y)(z) + (-3)(-2)(x⁻³)(x³)(y²)(y⁻²)(z⁴)
= -12x²y³z + 6x⁰y⁰z⁴
= -12x²y³z + 6z⁴
The final simplified expression is -12x²y³z + 6z⁴.
2) To multiply the polynomials 36a⁵b and 24a⁻²b⁷, we can apply the product rule for exponents.
36a⁵b * 24a⁻²b⁷
= (36 * 24)(a⁵ * a⁻²)(b * b⁷)
= 864a³b⁸
The simplified expression is 864a³b⁸.
(3) To factor the expression x³ + 3x² + 25x + 75 completely, we can check for possible rational roots using the rational root theorem. The possible rational roots are the factors of the constant term (75) divided by the factors of the leading coefficient (1).
The factors of 75 are ±1, ±3, ±5, ±15, ±25, and ±75.
The factors of 1 are ±1.
By testing these possible roots, we find that x = -3 is a root of the polynomial. Therefore, x + 3 is a factor.
Using synthetic division or long division, we can divide the polynomial x³ + 3x² + 25x + 75 by (x + 3) to obtain:
(x³ + 3x² + 25x + 75) / (x + 3)
= x² + 25
So the completely factored form of the expression is (x + 3)(x² + 25).
(4) To multiply the rational expressions (3x + 21) and (x² - 49), we can use the distributive property.
(3x + 21) * (x² - 49)
= 3x(x² - 49) + 21(x² - 49)
Using the distributive property, we can simplify further:
= 3x³ - 147x + 21x² - 1029
The final expression is 3x³ + 21x² - 147x - 1029.
(5) To multiply the rational expressions (12x²y⁷) / (18zw²) * (54z⁶w⁶), we can multiply the numerators and denominators separately:
(12x²y⁷ * 54z⁶w⁶) / (18zw²)
= (12 * 54 * x² * y⁷ * z⁶ * w⁶) / (18z * w²)
= (216x²y⁷z⁶w⁶) / (18zw³)
= 12x²y⁷z⁵w³
(6) To add or subtract the rational expressions, (7x - 5) / (5x - 13) - (2x - 3) / (2x - 3), we can combine the fractions since the denominators are the same:
[(7x - 5) - (2x - 3)] / (5x - 13)
= (7x - 5 - 2x + 3) / (5x - 13)
= (5x - 2) / (5x - 13)
(7) The equation 1/(1-x²) = 5/(x - 1) can be solved by cross-multiplication:
1 * (x - 1) = 5 * (1 - x²)
x - 1 = 5 - 5x²
x - 1 = 5 - 5x²
x - 1 - x + 5x² = 5
5x² - 2x - 6 = 0
Learn more about Polynomials here: brainly.com/question/11536910
#SPJ11