A building is constructed using bricks that can be modeled as right rectangular prisms with a dimension of
8
8 in by
3
1
2
3
2
1
in by
3
3 in. If the bricks cost $0.10 per cubic inch, find the cost of 1950 bricks. Round your answer to the nearest cent.

Answers
So the cost of 1950 bricks is $163.80.
For the given right rectangular prism,
Dimension = 8 in x 3\(\frac{1}{2}\) in x 3 in
Then,
Length = 8 in
Width = 3\(\frac{1}{2}\) in
Height = 3 in
Now find the volume of one brick by multiplying its length, width, and height together, so,
⇒ 8 in x 7/2 in x 3 in = 84 in³
Now calculate the total volume of 1950 bricks,
⇒ 1950 x 84 in = 163800 in³
Now we can find the total cost of the bricks by multiplying the total volume by the cost per cubic inch,
⇒ 163800 in x $0.10/in = $16,380.00
Finally, round our answer to the nearest cent,
we can divide by 100 and round to two decimal places,
⇒ $16,380.00 / 100 = $163.80
So the cost of 1950 bricks, rounded to the nearest cent, is $163.80.
Learn more about the multiplication visit:
https://brainly.com/question/10873737
#SPJ1
Related Questions
Help !! Pls :3:’dnmdnsnms

Answers
The congruent reason for the triangles is (b) HL theorem
How to determine the congruent statement?From the question, we have the following parameters that can be used in our computation:
Triangles = FGH and JHK
The SSS similarity theorem implies that the corresponding sides of the two triangles in question are not just similar, but they are also congruent
From the question, we can see that the following corresponding sides on the triangles:
Sides GH and HK
Sides FH and JK
These parameters are given in reasons (2) and (3) and it implies that these sides are congruent sides
For the triangle to be congruent by SSS, the following sides must also be congruent
GH must be congruent to HK
The above statement is true because point H is the midpoint of line GK
This is indicated in reason (2)
Hence, the congruent statement is SSS.
However, we can also make use of the HL theorem in (B)
Read more about congruent triangles at
brainly.com/question/1675117
#SPJ1
an object is thrown upward at a speed of 156 feet per second by a machine from a height of 19 feet off the ground. the height of the object after seconds can be found using the equation h= -16t^2 +156t +5. When will the height 269feet?. When will the object reach the ground?
Answers
Solving the quadratic equation, we found that the object is at a height of 269 feet when t is 1.99s and 8.55s and the object reaches the ground when t = 9.78s.
What is a quadratic equation?
Any equation in algebra that can be written in standard form:
ax² + bx + c =0
where x stands for an unknown value, where a, b, and c stand for known values, and where a 0 is true is known as a quadratic equation.
The given equation of height h = -16t² + 156t +5
a) The time when the height is 269 feet can be found by substituting this value for h in the above equation.
h = -16t² + 156t +5
169 = -16t² + 156t +5
16t² - 156t + 164 = 0
Solving we get t = 8.55 s, 1.99s
b) The time when the object reaches the ground.
For this, we can take h = 0
-16t² + 156t +5 = 0
t = -0.03, 9.78
The negative value can be ignored.
Therefore solving the quadratic equation, we found that the object is at a height of 269 feet when t is 1.99s and 8.55s and the object reaches the ground when t = 9.78s.
To learn more about quadratic equations, follow the link.
https://brainly.com/question/28038123
#SPJ4
how do i solve this absolute value equation
2|5x|= 10?
Answers
Answer:
x=1 x = -1
Step-by-step explanation:
2|5x|= 10
Divide each side by 2
2/2|5x|= 10/2
|5x|= 5
Absolute values have 2 solutions, one positive and one negative
5x = 5 5x = -5
Divide each side by 5
5x/5 = 5/5 5x/5 = -5/5
x = 1 x = -1
Answer:
Step-by-step explanation:
● 2|5x| = 10
● 2 × |5| ×x = 10
5 is positive so |5| = 5
● 2×5× |x| = 10
● 10×|x| = 10
● |x| = 10
● x = 1 or x = -1
Chase plays the piano and the cello for every 2 hours he practices the piano he practices the cello for 4 hours if he practice the piano for 7 hours last week how many hours did he spend practicing the cello
Answers
Answer:
9 hours
Step-by-step explanation:
if Chase practices 3hr of cello per every 2hrs of piano, first find how may times does 2hrs goes into the total 6hrs:
6 ÷ 2 = 3
Then multiply the number the hours of cello by the total 2 hours of 6;
3 × 3 = 9
so your final answer would be: 9 hours of cello
Hope this helps!
Have a nice day!
Answer:
14 Hours
Step-by-step explanation:
Divide 7 hours by 2 to get the 2-hour intervals in which he played piano.
7/2=3.5
Multiply this by 4 to get the amount of time he spends on the cello.
3.5*4=14
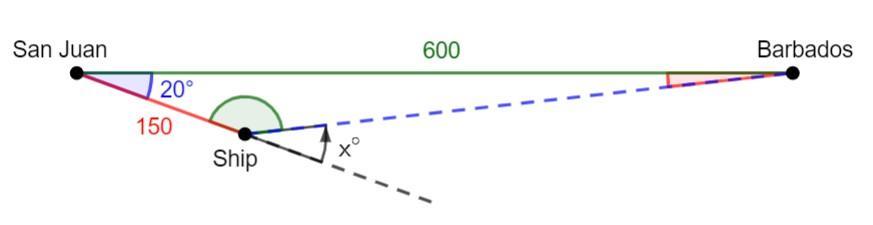
NO LINKS!! Part 8a: Please help me with this problem
THIS IS NOT MULTIPLE CHOICE!!!
a. Through what angle should the captain turn to head directly to Barbados?
b. Once the turn is made, how long will it be before the ship reaches Barbados if the same 15-knot speed is maintained?

Answers
Answer:
26.38° (nearest hundredth)
30.7960166... hours = 30 hours 47 mins 37 secs
Step-by-step explanation:
one knot = one nautical mile (nm) per hour
Therefore, 15-knot speed for 10 hours = 15 × 10 = 150 nm
Use cosine rule to find the distance between the ship and Barbados (blue dashed line on attached diagram).
Cosine rule: c² = a² + b² - 2ab cos(C)
Given:
a = 150b = 600C = 20°⇒ c² = 150² + 600² - 2(150)(600)cos(20°)
⇒ c² = 213355.3283...
⇒ c = 461.9040249... nm
Use sine rule to calculate smallest missing angle (red on attached diagram)
\(\sf \implies \dfrac{sin(A)}{150}=\dfrac{sin(20)}{461.9040249}\)
\(\sf \implies sin(A)=\dfrac{150sin(20)}{461.9040249}\)
\(\sf \implies A=6.376917848... \textdegree\)
Sum of interior angles of a triangle = 180°
⇒ missing interior angle (green) = 180° - 20° - 6.376917848...° = 153.6230822...°
Angles on a straight line sum to 180°
⇒ x° = 180° - 153.6230822...° = 26.376917848...°
The distance between the Ship and Barbados is 461.9040249 nm
Therefore, to calculate the time, divide the distance by the speed:
t = 461.9040249... ÷ 15 = 30.7960166... hours
PLSSS HELP ME 14 POINTS

Answers
The transformation of f(x) to g(x) is :
Vertically compressed by a factor of 9Shifted down by 2 Describing the transformation of the functionsFrom the question, we have the following parameters that can be used in our computation:
The functions f(x) and g(x)
Where, we have
f(x) = x
g(x) = 1/9x - 2
The graph of the functions f(x) and g(x) are added as an attachment
And we have the transformations to be:
Vertically compressed by a factor of 9Shifted down by 2Read more about transformation at
brainly.com/question/27224272
#SPJ1

A +3b identity each part of the algebraic expression
Answers
Answer:
3=coeffcient
b=variable
A=constant
Question 5 (2 points)
Bryce is exercising on a stationary bike. He burns 144 calories in 15 min. What's the
number of calories Bryce burns per minute?
8.9 calories/min
9.3 calories/min
9.6 calories/min
9,8 calories/min
Answers
Answer:
9.6 calories/min
Step-by-step explanation:
Here Bryce burns 144 calories in 15 mins
Therefore, For each min value you need to:- Divide the Total Number of calories by Total Time Taken
i.e. 144 calories / 15 min = 9.6 calories/min
To learn about calculations visit the side:-
<Alegbra>site:https:/brainly.com
Help me if you can please

Answers
Answer:
the question is not visible
Find a and b using the factor theorem.
\(f(x)=x^3+ax^2+bx-12\) has factor \((x-1), (x+1)\)
Answers
The values of a and b using the factor theorem for the polynomial f(x), we set f(1) and f(-1) equal to zero. Solving the resulting system of equations, we find that a = 12 and b = -1.
To find the values of a and b using the factor theorem, we need to use the given factors (x - 1) and (x + 1) and the fact that they are roots of the polynomial f(x).
The factor theorem states that if (x - c) is a factor of a polynomial, then f(c) = 0. Therefore, we can set x = 1 and x = -1 in the polynomial f(x) to get two equations.
First, let's substitute x = 1 into f(x):
f(1) = (1)^3 + a(1)^2 + b(1) - 12
f(1) = 1 + a + b - 12
Next, let's substitute x = -1 into f(x):
f(-1) = (-1)^3 + a(-1)^2 + b(-1) - 12
f(-1) = -1 + a - b - 12
Since (x - 1) and (x + 1) are factors, f(1) and f(-1) must equal zero. Therefore, we can set the two equations equal to zero and solve for a and b:
1 + a + b - 12 = 0
-1 + a - b - 12 = 0
Rearraning the equations, we have:
a + b = 11
a - b = 13
Now, we can solve this system of equations. Adding the two equations, we get:
2a = 24
a = 12
Substituting the value of a into one of the equations, we find:
12 - b = 13
b = -1
Therefore, the values of a and b are 12 and -1 respectively.
For more such questions on polynomial
https://brainly.com/question/1496352
#SPJ8
A beverage manufacturer is mixing up a 30% tomato juice blend. The manufacturer already
has 740 liters of a blend that contains 36% juice, to which some 26% juice will be added.
How much should be added to obtain the 30% tomato juice that is desired?
Write your answer as a whole number or as a decimal rounded to the nearest tenth.
liters
Submit
a
M
Answers
Answer:
1110 liters
Step-by-step explanation:
Let x = amount of 26% juice.
Amount of tomato juice:
740 liters of 36% juice contains 0.36(740) = 266.4 liters of tomato juice
x liters of 26% juice contains 0.26x liters of tomato juice
The result will be x + 740 liters of the juice blend at a concentration of 30%. It contains 0.3(x + 740) liters of tomato juice.
266.4 + 0.26x = 0.3(x + 740)
266.4 + 0.26x = 0.3x + 222
-0.04x = -44.4
x = 1110
Answer: 1110 liters
In circle O, secants ADB and AEC are drawn from external point A
such that points D, B, E, and C are on circle O. If AD = 8, AE = 6,
and EC is 12 more than BD, the length of BD is
(1) 6
(2) 22
(3) 36
(4) 48
Answers
The length of BD is 22.
In the given scenario, let's consider the following information.
AD = 8
AE = 6
EC is 12 more than BD.
To find the length of BD, we can utilize the Intercepted Arcs Theorem, which states that when two secants intersect outside a circle, the measure of an intercepted arc formed by those secants is equal to half the difference of the measures of the intercepted angles.
From the given information, we know that AD = 8 and AE = 6.
Since these are the lengths of the secants, we can use them to calculate the intercepted arcs.
First, let's find the intercepted arc corresponding to AD:
Intercepted Arc ADB = 2 \(\times\) AD = 2 \(\times\) 8 = 16
Similarly, we can find the intercepted arc corresponding to AE:
Intercepted Arc AEC = 2 \(\times\) AE = 2 \(\times\) 6 = 12
Now, we know that EC is 12 more than BD.
Let's assume the length of BD as x.
BD + 12 = EC
Now, let's consider the intercepted arcs theorem:
Intercepted Arc ADB - Intercepted Arc AEC = Intercepted Angle B - Intercepted Angle C
16 - 12 = Angle B - Angle C
4 = Angle B - Angle C.
Since Angle B and Angle C are vertical angles, they are congruent:
Angle B = Angle C.
Therefore, we can say:
4 = Angle B - Angle B
4 = 0
However, we have reached an inconsistency here.
The equation does not hold true, indicating that the given information is not consistent or there may be an error in the problem statement.
As a result, we cannot determine the length of BD based on the given information.
For similar question on length.
https://brainly.com/question/30582409
#SPJ8

What is the height of a parallelogram with area 56 m2, and a base of 7m
Answers
Answer: 392m^2
Step-by-step explanation:
Area of parallelogram is base x height
56 x 7 = 392m^2
D = {x:x is a factor of 12
Answers
Answer:
D={1,2,3,4,6,12}
Step-by-step explanation:
Factors of 12 are :-➜1
➜2
➜3
➜4
➜6
➜12
A restaurant on the top of a building is shaped like a circle with a radius of 80 feet. The restaurant rotate 60 degrees every 15 minutes. Two diners notice a bird that is sitting on a ledge outside of a window. If the bird stays on the ledge outside of a window, approximately how far will the bird travel in an hour?
Answers
Since, the restaurant rotates 60° every 15 minutes, then it will rotate 60°*4=240°
in one hour.
The full rotation of the restaurant is represented by 360°
Then,
\(\begin{gathered} \text{Circunference}=2\pi r \\ 2\pi r=2\pi\cdot80=160\pi \end{gathered}\)Having the length of the circunference, we know that 240° is only 2/3 from the full rotation, so the bird will travel in one hour:
\(160\pi\cdot\frac{2}{3}=335.1\text{ ft}\)Question 12 of 22
Select the action you would use to solve = 16. Then select the property that
justifies that action.
A. Property: Multiplication property of equality.
B. Action: Add 4 to both sides.
C. Property: Addition property of equality.
D. Action: Divide both sides by 4.
E. Property: Division property of equality.
OF Action: Multiply both sides by 4.
Answers
Answer:
The correct answer is:
D. Action: Divide both sides by 4.
E. Property: Division property of equality.
Solve for x: 3 (x - 3) + 8x = 5(2x + 1)
Answers
Answer:
x = 14
Step-by-step explanation:
3 (x - 3) + 8x = 5 (2x + 1)
FOIL: 3x - 9 + 8x = 10x +5
Move all the x terms to one side and all the constants to the other:
3x + 8x - 10x = 5 + 9
Combine like terms: x = 14
Suppose that a box contains 8 cameras and that 4 of them are defective. A sample of 2 cameras is selected at random. Define the random variable variable x as the number of defective cameras in the sample. What is the probability distribution for x?
Answers
The probability distribution for x is:
x P(x)
0 0.214
1 0.571
2 0.214
How can we determine the probability distribution for x?Since there are 8 cameras in the box, the total number of ways to choose 2 cameras from the box is given by the combination formula:
C(8,2) = 8!/(2!×(8-2)!) = 28
So there are 28 possible ways to choose a sample of 2 cameras.
Now, let's calculate the probability of each possible value of x:
When x = 0, both cameras in the sample are non-defective. The number of ways to choose 2 non-defective cameras from the 4 non-defective cameras in the box is given by the combination formula:
C(4,2) = 4!/(2!×(4-2)!) = 6
So the probability of x = 0 is:
P(x=0) = (number of ways to choose 2 non-defective cameras)/(total number of ways to choose 2 cameras)
= 6/28
= 0.214
When x = 1, one camera in the sample is defective and the other is non-defective. The number of ways to choose 1 defective camera from the 4 defective cameras in the box and 1 non-defective camera from the 4 non-defective cameras in the box is given by the product of the corresponding combinations:
C(4,1) × C(4,1) = 4×4 = 16
So the probability of x = 1 is:
P(x=1) = (number of ways to choose 1 defective camera and 1 non-defective camera)/(total number of ways to choose 2 cameras)
= 16/28
= 0.571
When x = 2, both cameras in the sample are defective. The number of ways to choose 2 defective cameras from the 4 defective cameras in the box is given by the combination formula:
C(4,2) = 4!/(2!×(4-2)!) = 6
So the probability of x = 2 is:
P(x=2) = (number of ways to choose 2 defective cameras)/(total number of ways to choose 2 cameras)
= 6/28
= 0.214
Therefore, the probability distribution for x is:
x P(x)
0 0.214
1 0.571
2 0.214
to know more about probability
brainly.com/question/30034780
#SPJ1
fine the nth term of 11,13,15,17
Answers
The nth term of 11,13,15,17 is,
⇒ T (n) = 9 + 2n
Given that;
The sequence is,
11, 13, 15, 17, ....
Here, Common difference is,
13 - 11 = 2
15 - 13 = 2
Hence, Sequence is in Arithmetic sequence.
So, the nth term of 11,13,15,17 is,
⇒ T (n) = a + (n - 1)d
⇒ T (n) = 11 + (n - 1) 2
⇒ T (n) = 11 + 2n - 2
⇒ T (n) = 9 + 2n
Thus, The nth term of 11,13,15,17 is,
⇒ T (n) = 9 + 2n
Learn more about the Arithmetic sequence visit:
https://brainly.com/question/6561461
#SPJ1
Multiply the product
(m+3)(m-3)
Answers

Answer:
The answer to (m+3)(m-3) is m^2-9.
Step-by-step explanation:
We will use distributive law to solve this question.
m(m-3)+3(m-3)
= m^2-3m+3m-9
= m^2-9 (since, 3m-3m=0)
As an alternative method, we can use the direct rule learned in algebra: (a+b)(a-b)=a^2-b^2.
so, here a=m and b=3.
(m+3)(m-3)
=m^2-3^2
=m^2-9
PLEASE HURRY!!! what is the slope of the graph?

Answers
Step-by-step explanation:
2..................pls follow me
cos(0)=square root 3/3, sin 0<0. what is the value of sin0
Answers
Answer:
sin θ = \(\frac{\sqrt{6} }{3}\)
Step-by-step explanation:
Given that,
cos θ = \(\frac{\sqrt{3} }{3}\)
From the trigonometric functions,
cos θ = \(\frac{adjacent}{hypotenus}\)
⇒ adjacent = \(\sqrt{3}\), and the hypotenuse = 3
Let the opposite side be represented by x, applying the Pythagoras theorem we have;
\(/hyp/^{2}\) = \(/adj/^{2}\) + \(/opp/^{2}\)
\(/3/^{2}\) = \((\sqrt{3} )^{2}\) + \(x^{2}\)
9 = 3 + \(x^{2}\)
\(x^{2}\) = 9 - 3
= 6
x = \(\sqrt{6}\)
Thus, opposite side = \(\sqrt{6}\)
So that,
sin θ = \(\frac{opposite}{hypotenuse}\)
= \(\frac{\sqrt{6} }{3}\)
Therefore,
sin θ = \(\frac{\sqrt{6} }{3}\)
Here are the heights (in inches) of 12 students in a seminar. 71, 67, 62, 60, 70, 64, 68, 72, 58, 63, 60, 66 What is the percentage of these students who are shorter than 65 inches? 1% X 5
Answers
25% of the students in the seminar are shorter than 65 inches.
To find the percentage of students who are shorter than 65 inches, we first need to find the number of students whose height is less than 65 inches:
There are three students who are shorter than 65 inches: 62, 60, and 58.
Therefore, the percentage of students who are shorter than 65 inches is:
(3 students / 12 students) × 100% = 25%
Note that the value given for 1% × 5 does not appear to be relevant to this question, and is not necessary for the calculation of the percentage of students who are shorter than 65 inches.
For such more questions inches
https://brainly.com/question/876758
#SPJ8
Nonsense will be reported!!

Answers
Answer:
See below
Step-by-step explanation:
d = 78° (Vertical angles)
h = 70° (Vertical angles)
Measure of angles d and h are are not equal. therefore they are not congruent.
Suppose the function h(x) = 2x - 9 is translated up 5 units to become a new function,
Xx). What's the equation of the new function?
A) x) = 7x-4
B)(x) = 2x - 14
C)(x) = 7x-9
D) (x)=2x-4
Answers
According to the given data the equation of the new function is (D) f(x) = 2x - 4.
What is meant by equation?An equation is a mathematical statement that indicates that two expressions are equal. It contains an equals sign "=" and may involve variables, constants, and mathematical operations such as addition, subtraction, multiplication, division, exponentiation, etc.
According to the given information:If we translate the function h(x) = 2x - 9 up by 5 units, the new function f(x) will have the form:
f(x) = h(x) + 5
Substituting the definition of h(x) into this equation, we get:
f(x) = 2x - 9 + 5
Simplifying, we have:
f(x) = 2x - 4
Therefore, the equation of the new function is (D) f(x) = 2x - 4.
To know more about equations visit:-
https://brainly.com/question/22964920
#SPJ1
Which linear equation is in standard form? A) y = mx + b B) Ax + By = C C) y - y1 = m(x - x1) D) x - x1 y - y1 = m
Answers
Answer: B (\(Ax + By = C\)).
Answer:
B
Step-by-step explanation:
Ax + By = C
Dominique is buying juice. She needs 2 liters. A half-liter of juice costs $2.91. A 200-milliliter container of juice costs $1.19. What should Dominique buy so she gets 2 liters at the lowest price? Explain.
Answers
Answer:
Dominique should buy 4 200-milliliter containers of juice. This will cost her $4.76, which is the lowest price for 2 liters of juice. By buying the smaller containers, Dominique can save $0.45 compared to buying the larger container.
the diffrence of 54 and 32 mutlipted by the diffrence of 8 and 5
Answers
Answer:
66
Step-by-step explanation:
the difference of 54 and 32 is 54 - 32 = 22
the difference of 8 and 5 is 8 - 5 = 3
then
22 × 3 = 66
Triangle ABC is an isosceles triangle. Angle A is the vertex angle. AB=8x-8 and AC=6x+9 find the length of one of the legs
Answers
Answer:
tge length is 14 make me brainliest
Step-by-step explanation:
I did it in a test and hit it correct
What is 0.024 + 0.003 in words
Answers
Answer:
Step-by-step explanation:
two hundredths four thousandths +three thousandths = two hundredths seven thousandths