A= 3/4-1/2B=5/4+6/4C=12/4-4/8D=2/8+1/4CODE= A+BCODE=C-DCODE=A+B+C+DWhat is the answer for the 3 codes?
Answers
hello
let's start by simplifying A,B and C before solving for each code
\(\begin{gathered} A=\frac{3}{4}-\frac{1}{2} \\ A=\frac{1}{4} \\ A=0.25 \end{gathered}\)Related Questions
Was it evaluated correctly?
Explain your reasoning

Answers
prime factorisation 545 divisible method
Answers
Answer:
Prime Factors of 545 are 5, 109, and usually expressed as 5 x 109. 4.
hope this is right! :) -liaa
What is the reciprocal of
5/6
Answers
Answer:
6/5
Step-by-step explanation:
Create an expression that has the same value as (6x-4) + (x + 5).
Write the correct numbers from the list in the blank boxes. Each number
may be used once, more than once, or not at all.
Answers
Answer: 7x + 1
Step-by-step explanation:
(6x-4)+(x+5)
Step 1: Remove Parentheses:
6x-4+x+5
Step 2: Combine Like Terms:
7x +1
For each of the following vector fields
F, decide whether it is conservative or not by computing the appropriate first order partial derivatives. Type in a potentialfunction f (that is, ∇f = F) with f(0,0)=0. If it is not conservative, type N.
A. F(x,y)=(−16x+2y)i+(2x+10y) j f(x,y)= _____
B. F(x,y)=−8yi−7xj f(x,y)=_____
C. F(x,y)=(−8sin y)i+(4y−8xcosy)j f(x,y)=_____
Answers
(A)
\(\dfrac{\partial f}{\partial x}=-16x+2y\)
\(\implies f(x,y)=-8x^2+2xy+g(y)\)
\(\implies\dfrac{\partial f}{\partial y}=2x+\dfrac{\mathrm dg}{\mathrm dy}=2x+10y\)
\(\implies\dfrac{\mathrm dg}{\mathrm dy}=10y\)
\(\implies g(y)=5y^2+C\)
\(\implies f(x,y)=\boxed{-8x^2+2xy+5y^2+C}\)
(B)
\(\dfrac{\partial f}{\partial x}=-8y\)
\(\implies f(x,y)=-8xy+g(y)\)
\(\implies\dfrac{\partial f}{\partial y}=-8x+\dfrac{\mathrm dg}{\mathrm dy}=-7x\)
\(\implies \dfrac{\mathrm dg}{\mathrm dy}=x\)
But we assume \(g(y)\) is a function of \(y\) alone, so there is not potential function here.
(C)
\(\dfrac{\partial f}{\partial x}=-8\sin y\)
\(\implies f(x,y)=-8x\sin y+g(x,y)\)
\(\implies\dfrac{\partial f}{\partial y}=-8x\cos y+\dfrac{\mathrm dg}{\mathrm dy}=4y-8x\cos y\)
\(\implies\dfrac{\mathrm dg}{\mathrm dy}=4y\)
\(\implies g(y)=2y^2+C\)
\(\implies f(x,y)=\boxed{-8x\sin y+2y^2+C}\)
For (A) and (C), we have \(f(0,0)=0\), which makes \(C=0\) for both.
please help asap!!!!!

Answers
Answer:
angle RQS
Step-by-step explanation:
Which of the following statements best describes a theorem?
A. A theorem cannot be proven.
B. A theorem can be false.
C. A theorem is always true.
D. A theorem is never true.
Answers
Answer:
a
Step-by-step explanation:
A theorem cannot be proven.
Submit your answers to the following questions. Be sure to explain your reasoning for each; it is helpful to draw this out to get started to see any quantitative patterns that develop.
If you write the counting numbers in rows of 7 numbers each, like shown below (but you keep going), where all the number line up in seven vertical columns as you go. (Note in the example below, the number 13 is in the 2nd row and the 6th column.)
1 2 3 4 5 6 7
8 9 10 11 12 13 14
15 16 17 18 19 20 21
In which column would the number 100 land?
In which row?
Now write the counting numbers in rows of 6 numbers each. What’s the location of 100 in this array?
Write arrays with other length rows. Find a way to predict in which row and column 100 will land for any array of numbers.
Answers
The number 100 would land in column 2
The number 100 would land in row 14The location of 100 in rows of 6 numbers is row 16 and column 3The location of 100 in rows of n numbers is row q and column rIn which column would the number 100 land?Given that we have the array of numbers
The length of each row in the array is 7
Dividing 100 by 7, we have
100/7 = 14 Remainder 2
This means that
Column = 2
In which row would the number 100 land?In (a), we have
100/7 = 14 Remainder 2
This means that
Row = 14
The location of 100 in rows of 6 numbersHere, we have
The length of each row in the array is 6
Dividing 100 by 6, we have
100/6 = 16 Remainder 3
So, the location of 100 in rows of 6 numbers is row 16 and column 3
Predicting the row and column 100 will landLet the length of each row in the array be n
Dividing 100 by n, we have
100/n = q Remainder r
This means that the location of 100 in rows of n numbers is row q and column r
Read more about numbers at
https://brainly.com/question/20372424
#SPJ1
Peter is practicing how to apply the distributive property. In which example(s) did Peter NOT correctly apply the distributive property?

Answers
Answer:
mn
Step-by-step explanation:jhhh
given that tan(θ)=5/8 and θ is in quadrant i find and cos (θ/2)
Answers
Recall the half-angle identity for cosine,
cos²(θ/2) = (1 + cos(θ))/2
Since θ lies in quadrant I, we also have θ/2 in quadrant I, since
0 < θ < π/2 ⇒ 0 < θ/2 < π/4
Then for this θ, we have
cos(θ/2) = + √((1 + cos(θ))/2)
Also recall the Pythagorean identity,
cos²(θ) + sin²(θ) = 1
Multiplying through both sides of this identity by cos²(θ) gives another form of it,
1 + tan²(θ) = sec²(θ)
Because θ belongs to quadrant I, we know cos(θ) > 0, so we also have sec(θ) = 1/cos(θ) > 0.
It follows that
sec(θ) = + √(1 + tan²(θ)) = √89/8
⇒ cos(θ) = 8/√89
and so
cos(θ/2) = + √((1 + 8/√89)/2) = √(1/2 + 4/√89)
stephine puts 30 cubes in a box.the cubes are 1/2 inch on each side.the box holds 2 layers with 15 cubes in each layer.what is the volume of the box
Answers
The Volume of the box is 3.75in³
Volume of a cubeThe volume of the box is dependent on the volume of the cube in it.
To obtain the volume of a cube, we use the relation, V = s³
s = side of the cube
For each cubeVolume = 0.5³ = 0.125 in³
Number of cubes in box = 30
Volume of the boxVolume of each cube × Number of cubes
0.125 × 30 = 3.75 in³
Hence, the volume of the box is 3.75in³
Learn more on Volume ; brainly.com/question/27710307
#SPJ1
Suppose that continuous random variables X and Y have a joint probability density function given by: f X,Y
(x,y)={ c⋅x 2 y,0,0≤x≤2;0≤y≤2 otherwise 1. Define the mode of a continuous random variable to be the point at which the density is maximized, if such a point exists. What is the mode of YY?
2. What value of cc makes this a valid probability density function?
3. What is the expected value of YY, E[Y]E[Y]?
4. What is the variance of YY, V[Y]V[Y]?
Answers
And , the Y's variance is \(V[Y] = E[Y^2] - (E[Y])^2 = 2 - 1^2 = 1.\)To find the mode of Y, we need to find the value of y that maximizes the joint probability density function\(f_X, Y(x,y).\)
To do this, we can fix x to be a particular value and then find the value of y that maximizes \(f_X, Y(x,y).\)
For any fixed x between 0 and 2, the function\(f_X, Y(x,y)\) is maximized at y = 1, since this is the only value of y that depends on x and maximizes the function\(cx^2y.\) Therefore, the mode of Y is 1.
To find the value of c that makes this a valid probability density function, we need to ensure that the integral of \(f_X, Y(x,y)\)over the entire sky-plane is equal to 1. We can set up the integral as follows:
integral from 0 to 2 of (integral from 0 to 2 of cx^2y dy) dx
= integral from 0 to \(2 of [c*x^2/2 * y^2]\)evaluated from 0 to 2 dx
= integral from 0 to 2 of \(c*x^2 x2d\)
= [2c/3 * x^3] evaluated from 0 to 2
= (16c/3)
For this to equal 1, we must have c = 3/16. Therefore, the valid probability density function is:
f_X,Y(x,y) = { (3/16)x^2y, 0 <= x <= 2, 0 <= y <= 2; 0, otherwise }
To find the expected value of Y, we need to integrate Y times the joint probability density function f_X, Y(x,y) over the entire xy-plane:
E[Y] = integral from 0 to 2 of (integral from 0 to 2 of y*f_X, Y(x,y) dy) dx
= integral from 0 to 2 of \([(3/16)*x^2/2 * y^2]\) evaluated from 0 to 2 dx
= integral from 0 to 2 of (3/16)*x^2 dx
= [3/16 * x^3/3] evaluated from 0 to 2
= 1
Therefore, the expected value of Y is 1.
To find the variance of Y, we first need to find the second moment of Y by integrating Y^2 times the joint probability density function f_X, Y(x,y) over the entire xy-plane:
E[Y^2] = integral from 0 to 2 of (integral from 0 to 2 of y^2*f_X, Y(x, y) dy) dx
= integral from \(0 to 2 of [(3/16)*x^2/3 * y^3]\) evaluated from 0 to 2 dx
= integral from \(0 to 2 of (3/8)*x^2 dx\)
= \([3/8 * x^3/3]\) evaluated from 0 to 2
= 2
And , the Y's variance is
\(V[Y] = E[Y^2] - (E[Y])^2 = 2 - 1^2 = 1.\)
To know more about the variance
brainly.com/question/14116780
#SPJ4
use the function f(x) = 3x+8. evaluate the function for f(1). 8, 11, 3
Answers
Answer: 11
Step-by-step explanation:
F(1) = 3(1) + 8
F(1) = 3 + 8
F(1) = 11
You just substitute the x in for 1 and solve from there.
me ayudan a resolver esto?

Answers
Step-by-step explanation:
es 1
6/9+2/3+10/2(5)=
6+6+45/9=
57/9
es 2
-3/6-2/4-10/5(2)=
-6-6-24/12=
36/12=3
es 3
15/8-3/2+8/9=
135-108+64/72=
91/72
1. margie's parents have invested $900 into a puppy so that she could still have him when she's older. If the money grows at a simple interest rate of 3% for the next 10 years how much will the original investment have grown
Answers
\(~~~~~~ \textit{Simple Interest Earned Amount} \\\\ A=P(1+rt)\qquad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{original amount deposited}\dotfill & \$900\\ r=rate\to 3\%\to \frac{3}{100}\dotfill &0.03\\ t=years\dotfill &10 \end{cases} \\\\\\ A = 900[1+(0.03)(10)] \implies A = 1170~\hfill \stackrel{ \textit{it grew by} }{\text{\LARGE 270}}\)
1.8 + 3.5y + 0.9 + 9 = 16.2
Answers
Answer:
Its about 1.3
Step-by-step explanation:
3.5y=16.2-1.8-0.9-9
3.5y=16.2-11.7
3.5y=4.5
Divide through by 3.5 to get y
3.5y/3.5=4.5/3.5
y=1.2857
QUESTION 23 What does a BER of 10-5 mean? a. there will be no errors during transmission since the BER is so low b. does not mean anything unless associated with a transmission data rate (bit rate) c. there is a probability of one error for every 100,000 bits transmitted d. None of the above
Answers
Answer:
c. there is a probability of one error for every 100,000 bits transmitted
Step-by-step explanation:
What does a BER of 10-5 mean?
a. there will be no errors during transmission since the BER is so low b. does not mean anything unless associated with a transmission data rate (bit rate) c. there is a probability of one error for every 100,000 bits transmitted d. None of the above
BER is an abbreviation for bit error rate.
BER is the percentage of bits with errors divided by the total number of bits that have been transmitted, received or processed over a given time period.
The rate is typically expressed as 10 to the negative power.
BER is the digital equivalent to signal-to-noise ratio in an analog system.
In this case \(10^{-5}\) is the same as writing \(1 \times10^{-5}\) which means there is a probability of 1 error for every 100,000 bits transmitted.
elm st. and spruce st. are parallel what is m<1

Answers
Answer:
The measure is 68
Step-by-step explanation:
180-112 = 68
side alternate exterior (supplementary)
The measure of angle 1 will be equal to 68.
What are supplementary angles?The angle is defined as the span between two intersecting lines or surfaces at or close to the point where they meet. The supplementary angle is defined as the angle having the sum of 180 degrees.
Given that there are two parallel lines intersecting one line at an angle of 112. The angle 1 will be calculated as:-
The angle will be calculated as follows:-
∠1 + 112 = 180
∠1 = 180 - 112 = 68
Therefore, the measure of angle 1 will be equal to 68.
To know more about supplementary angles follow
https://brainly.com/question/2046046
#SPJ5
A grocery store sells four different sizes of a popular brand of corn flakes. For the past few years the proportion of boxes they sell of each size has been quite stable: 10% Small, 15% Medium, 60% Large, and 15% Jumbo. They decide to change the pricing of the four sizes and want to see if this changes the proportion of boxes they sell of each size. To test this, a few weeks after changing the prices they take a simple random sample of 120 transactions involving corn flakes and count how many boxes of each size were sold. Here are the results:
Observed number of boxes sold for each box size
Small Medium Large Jumbo
8 24 61 27
Required:
a. We wish to carry out a test of significance to see if the distribution of sizes of cereal boxes soldhas changed. State the null and alternative hypotheses for this test.
b. Find the expected counts for each size box under the assumption that the null hypothesis is true.
Answers
The sale of the four different sizes is an illustration of the Goodness of Fit Tests
The expected counts for each size box are 0.8, 3.6, 36.6 and 4.05 respectively
The null and the alternate hypothesesThe null hypothesis is always represented by the equality sign i.e. 0 change or no change.
While the alternate hypothesis is always represented by an inequality.
So, the null and the alternate hypotheses are:
Null hypothesis; H0 : The distribution of sizes of all boxes sold of this brand of cereal did not change when the prices changed.Alternate hypothesis; Ha: The distribution of sizes of all boxes sold of this brand of cereal changed when the prices changed.The expected counts for each size boxThis calculated as:
E(x) = np
So, we have:
Small = 8 * 10% = 0.8
Medium = 24 * 15% = 3.6
Large = 61 * 60% = 36.6
Jumbo = 27 * 15% = 4.05
Hence, the expected counts for each size box are 0.8, 3.6, 36.6 and 4.05 respectively
Read more about expected values at:
https://brainly.com/question/15858152
6 people will attend a lunch 2 cans of juice should be provided per person determine the total number of cans of juice required
Answers
Answer:
12
Step-by-step explanation:
it's 6 people and 2 cans of juice goes to each person so you can multiply 6× 2 and you get 12 . 12 cans of juice would be required to provide 6 people with 2 cans each .
Which line is perpendicular to 3y + 2x = 9?
Options:
6x - 4y = 12
2x + 3y = 6
y + 3x = -2
y = -2x + 6
Answers
Answer:
2x + 3y = 6
Step-by-step explanation:
How much more expensive is it, per pound, to buy ground beef at Store B than at Store A?

Answers
Answer:
2.42
Step-by-step explanation:
First you need to use two points from store b to find the slope (y1-y2)/(x1-x2). I chose the first two points. (15.54-25.9)/(1.5-2.5)= 10.36. After you take another point from store b to plug into the equation y1-y2=m (x1-x2). M is the slope we just found and I used the first point.
Y1-15.54=10.36 (x1-1.5) distribute the 10.36 to the parentheses.
Y1-15.54=10.36x -15.54 get y1 by itself
Y=10.36x so store b is 10.36 a pound and store a is 7.94 a pound. 10.36-7.94= 2.42
solve the equation
a) y''-2y'-3y= e^4x
b) y''+y'-2y=3x*e^x
c) y"-9y'+20y=(x^2)*(e^4x)
Answers
Answer:
a) To solve the differential equation y''-2y'-3y= e^4x, we first find the characteristic equation:
r^2 - 2r - 3 = 0
Factoring, we get:
(r - 3)(r + 1) = 0
So the roots are r = 3 and r = -1.
The general solution to the homogeneous equation y'' - 2y' - 3y = 0 is:
y_h = c1e^3x + c2e^(-x)
To find the particular solution, we use the method of undetermined coefficients. Since e^4x is a solution to the homogeneous equation, we try a particular solution of the form:
y_p = Ae^4x
Taking the first and second derivatives of y_p, we get:
y_p' = 4Ae^4x
y_p'' = 16Ae^4x
Substituting these into the original differential equation, we get:
16Ae^4x - 8Ae^4x - 3Ae^4x = e^4x
Simplifying, we get:
5Ae^4x = e^4x
So:
A = 1/5
Therefore, the particular solution is:
y_p = (1/5)*e^4x
The general solution to the non-homogeneous equation is:
y = y_h + y_p
y = c1e^3x + c2e^(-x) + (1/5)*e^4x
b) To solve the differential equation y'' + y' - 2y = 3xe^x, we first find the characteristic equation:
r^2 + r - 2 = 0
Factoring, we get:
(r + 2)(r - 1) = 0
So the roots are r = -2 and r = 1.
The general solution to the homogeneous equation y'' + y' - 2y = 0 is:
y_h = c1e^(-2x) + c2e^x
To find the particular solution, we use the method of undetermined coefficients. Since 3xe^x is a solution to the homogeneous equation, we try a particular solution of the form:
y_p = (Ax + B)e^x
Taking the first and second derivatives of y_p, we get:
y_p' = Ae^x + (Ax + B)e^x
y_p'' = 2Ae^x + (Ax + B)e^x
Substituting these into the original differential equation, we get:
2Ae^x + (Ax + B)e^x + Ae^x + (Ax + B)e^x - 2(Ax + B)e^x = 3xe^x
Simplifying, we get:
3Ae^x = 3xe^x
So:
A = 1
Therefore, the particular solution is:
y_p = (x + B)e^x
Taking the derivative of y_p, we get:
y_p' = (x + 2 + B)e^x
Substituting back into the original differential equation, we get:
(x + 2 + B)e^x + (x + B)e^x - 2(x + B)e^x = 3xe^x
Simplifying, we get:
-xe^x - Be^x = 0
So:
B = -x
Therefore, the particular solution is:
y_p = xe^x
The general solution to the non-homogeneous equation is:
y = y_h + y_p
y = c1e^(-2x) + c2e^x + xe^x
c) To solve the differential equation y" - 9y' + 20y = x^2*e^4x, we first find the characteristic equation:
r^2 - 9r + 20 = 0
Factoring, we get:
(r - 5)(r - 4) = 0
So the roots are r = 5 and r = 4.
The general solution to the homogeneous equation y" - 9y' + 20y = 0 is:
y_h = c1e^4x + c2e^5x
To find the particular solution, we use the method of undetermined coefficients. Since x^2*e^4x is a solution to the homogeneous equation, we try a particular solution of the form:
y_p = (Ax^2 + Bx + C)e^4x
Taking the first and second derivatives of y_p, we get:
y_p' = (2Ax + B)e^4x + 4Axe^4x
y_p'' = 2Ae^4x +
Side 2. What is the sogel
What is the slope between the
points (2, 150) and (5,375)?
Answers
Answer:
75
Step-by-step explanation:
Use the slope formula (rise/run):
\(\frac{y_{2} - y_{1}}{x_{2} - x_{1}}\)
(375 - 150)/(5-2) = 225/3 = 75
Helping to give out points!! Whoever solves the math riddle correctly with a brief explanation will get brainliest and a thanks (the other answers will just get a thanks).
Riddle: I have a big family. I am 16 years old. My sister Reina is 22 years old. The twins are 14 years old. Susana is 10 years old and my brother Robert is 7 years old. If the total number of our ages added together is 100, how old is Albert?
Answers
Answer:
Robbert is 7
Step-by-step explanation:
because you already said it
(extra text for character minimum)
Joyce saved $220 on an item that was 75% off what was the original price
Answers
Answer:
$880
Step-by-step explanation:
Use the equation:
\(P=(1-d)x\) with d being the discount in a decimal form, and P being the price that was bought at.
220=(1-0.75)x
simplify parenthesis terms
220=0.25x
divide both sides by 0.25
880=x
So, the original price was $880.
Hope this helps! :)
Can y’all pls help me solve this!!
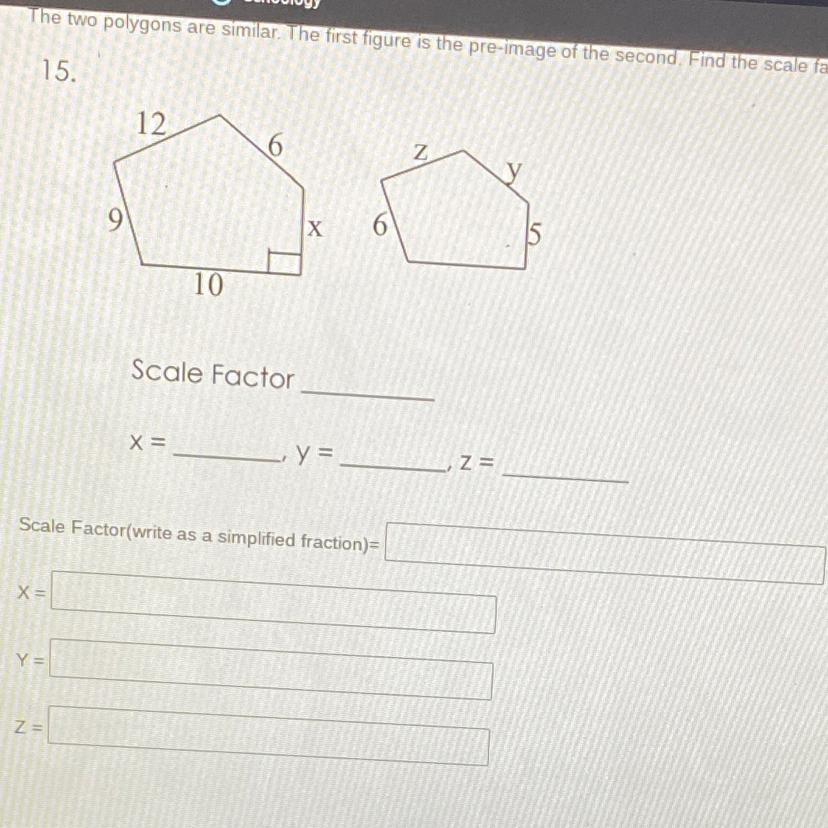
Answers
scale factor = 1.5
X = 7.5
Y = 4
Z = 8
Explanation
1. You can find the scale factor by dividing
9/6, which is 1.5. I divided 9 and 6 because they are congruent.
2. You can find x by using the proportion 9/6 = x/5, or 3/2 = x/5 which lets you work with smaller numbers. I’ll use the second proportion. Cross multiplying would give you 2x =15. To get the variable by itself divide both sides by 2, which leaves you with x = 7.5.
3. Use the proportion 3/2 = 6/y to solve for y. Cross multiplying would give you 12 = 3y. Divide both sides by 3 to get the variable by itself leaving you y = 4.
4. Use the proportion 3/2 = 12/z to solve for z. Cross multiplying would give you 24 = 3z. Divide both sides by 3 to get the variable by itself leaving z = 8.
Can someone help? CROWN TO BEST ANSWER
Can you write me a quantitative survey or simulation question(s)? Making it a little bit complex and not too simple?
This is relating to probability and statistics and I have to answer and collect data on them.
If you write a very good one you get a crown!! but it must be well written and a good question not just how much cars are there each morning?
Answers
Here are some examples of quantitative survey or simulation questions:
On a scale of 1 to 5, how likely are you to recommend our product to a friend or colleague?
1 (Not at all likely)
2
3
4
5 (Extremely likely)
How often do you use our app?
Daily
3-4 times a week
Once a week
Once every two weeks
Rarely
How much time do you spend using our app in an average day?
Less than 30 minutes
30 minutes to 1 hour
1 to 2 hours
More than 2 hours
How satisfied are you with the overall performance of our app?
Very dissatisfied
Dissatisfied
Neutral
Satisfied
Very satisfied
How do you rate the usability of our app?
Poor
Fair
Good
Very good
Excellent
What is a survey?A quantitative survey uses statistics to gather facts and figures. It's most frequently utilized to support or refute a conclusion you may have reached after conducting qualitative research.
A survey may be qualitative, quantitative, or a combination of the two. A quantitative survey is one that uses a questionnaire with scaleable responses. If your survey has descriptive questions with in-depth answers then it is a qualitative survey. Your survey is a mixed-method survey if it uses both of them.
Learn more about survey on:
https://brainly.com/question/14610641
#SPJ1
Enter the exact values of the trigonometric ratios in the boxes.
sin 45°
cos 30
tan 60
=

Answers
The required value of trigonometric ratios is,
sin 45° = 1/\(\sqrt{2}\)
cos 30 = \(\sqrt{3}\)/2
tan 60 = 1/ √3
We know that,
Trigonometric ratios are based on the value of the ratio of sides of a right-angled triangle and contain the values of all trigonometric functions. The trigonometric ratios of a given acute angle are the ratios of the sides of a right-angled triangle with respect to that angle.
Therefore,
sin 45° = 1/\(\sqrt{2}\)
cos 30 = \(\sqrt{3}\)/2
tan 60 = 1/ √3
To learn more about triangles visit:
brainly.com/question/1058720
#SPJ1
What is the GCF (Greatest Common Factor) of 30x and 45x?
Answers
Answer:
15x
Step-by-step explanation:
Both of these numbers can be divided by 15x.
If this helps please mark as brainliest