7 Theodore and Pam are rolling
out modeling clay for an activity in
art class. Theodore rolled out his
clay until it was 5 inches long
Pam rolled hers times as far
Did Pam roll her clay out less
than, more than, or the same as
Theodore?
Answers
Related Questions
what is the algebraic expression for: the quotient of 5 and y added to 3 is at least 5
Answers
the quotient of 5 and y: 5÷y
added to 3: 3 + 5÷y
is at least (AKA is greater than or equal to) 5: 3 + 5÷y ≥ 5
Answer: 3 + 5÷y ≥ 5
A quality control process finds 29.1 defects for every 9,700 units of production. What percent of the production is defective?
Answers
Given:
defective units = 29.1
total production = 9,700
Hence:
\(\%=\frac{portion}{total}\times100\)substituting values in the formula:
\(\%=\frac{29.1}{9700}\times100=0.3\%\)ANSWER
0.3 percent of the production is defective.
Determine the equation of the quadratic with zeros x = 1 and x = 5 passing through the
point (3,-12).
Please help
Answers
Answer:
\(y=3x^{2} -18x+15\) is the equation the quadratic as per the given conditions.
Step-by-step explanation:
Let the equation of the quadratic be:
\(y=ax^{2} +bx+c\)
Given that it has zeroes at x = 1 and x = 5 i.e. y = 0 at both the values of x.
Also passes through point (3, -12). i.e. when x = 3, y = -12
Putting x = 1, y = 0:
\(\Rightarrow a\times 1^{2} +b\times 1+c=0\\\Rightarrow a+b+c=0 ....... (1)\)
Putting x = 5, y = 0:
\(\Rightarrow a\times 5^{2} +b\times 5+c=0\\\Rightarrow 25a+5b+c=0 ....... (2)\)
Putting x = 3, y = -12:
\(\Rightarrow a\times 3^{2} +b\times 3+c=-12\\\Rightarrow 9a+3b+c=-12 ....... (3)\)
Equation (2) - Equation (1):
\(24a+4b=0\\\Rightarrow 6a +b=0 ...... (4)\)
Equation (2) - Equation (3):
\(16a+2b=12\\\Rightarrow 8a +b=6 ...... (5)\)
Equation (5) - Equation (4):
\(2a=6\\\Rightarrow a =3\)
Putting value of a in equation (4):
\(6\times 3+b=0\\\Rightarrow b = -18\)
Putting a and b in equation (1):
\(3-18+c=0\\\Rightarrow c= 15\)
So, the quadratic equation is:
\(y=3x^{2} -18x+15\)
PLS HELP DUE TODAY i will give brailest if you show all work please help



Answers
Answer:
15) 3(4+r)=-18
3x4+3xr
12+3r= -18
-12 -12
3r= -30
/3 /3
r= -10
Step-by-step explanation:
distribute the 3 to the 4 and the r you should then have 12+3r=-18 and so subtract from both sides 12 and you should have 3r=-30 divide both sides by 3 and you get your answer r=-10
Answer:
(7) n=9
8) x=8
9) m=-7
10) b= -6
11) r=6
12)b=10
13)v=8
14)k=-8
15)r=-10
16)p=20
17)v=10
18)x=21
19)a=28
20)b=10
Step-by-step explanation:
I need help with this equation

Answers
Step-by-step explanation:
4 x^2 - 64 = 0 re-wrire by adding 64 to both sides of the equation
4x^2 = 64 now just divide both sides by 4
x^2 = 16 that is the first part.....now sqrt both sides
x = +- 4
Answer: x^2 = 16, x = ±4
Step-by-step explanation:
Part 1: Starting with 4x^(2) - 64 = 0:
Add 64 to both sides to isolate the x^2 term:
4x^(2) = 64
Divide both sides by 4 to get x^(2) by itself:
x^(2) = 16
So we can rewrite 4x^(2) - 64 = 0 as x^(2) = 16.
Part 2: To solve x^(2) = 16, we take the square root of both sides:
x = ±√16
x = ±4
So the solution set for the equation 4x^(2) - 64 = 0 is {x = -4, x = 4}.
simplify this expression 4x^2 y^3 × 2x^3 y^4
Answers
Answer:
8x⁵y⁷
Step-by-step explanation:
4x²y³ × 2x³y⁴ = 8x⁵y⁷
Assume you deposited $3,200 in an account two years ago and are depositing another $5,000 today. You will make a final deposit of $3,500 one year from now. What will your account balance be three years from now if the account pays 4.85 percent interest, compounded annually?
Multiple Choice
$13,033.95
$14,328.90
$12,431.05
$13,666.10
$13,430.84
Answers
The account balance three years from now will be $13,666.10. So, the correct option is D) $13,666.10.
To calculate the account balance after three years, you can use the formula: A = P(1 + r/n)^(nt)where A is the final amount, P is the principal amount, r is the annual interest rate (as a decimal), n is the number of times the interest is compounded per year, and t is the time (in years).In this question, the principal amount (P) is $3,200 + $5,000 + $3,500 = $11,700. The annual interest rate (r) is 4.85%, compounded annually (n = 1) for three years (t = 3). Therefore, plugging the values into the formula, we get A = $11,700(1 + 0.0485/1)^(1×3)Simplifying the expression: A = $11,700(1.0485)^3A = $13,666.10For more such questions on account balance
https://brainly.com/question/28699158
#SPJ8
Determine if the following system of equations has no solutions, infinitely many
solutions or exactly one solution.
-3x + 4y = -5
-6x+8y= -10
a. One Solution
b. No Solutions
c. Infinitely Many Solutions
Answers
The system of Linear Equation has Infinitely Many Solutions
What is Linear Equation in Two Variables?
A linear equation in two variables is one that is stated in the form ax + by + c = 0, where a, b, and c are real integers and the coefficients of x and y, i.e. a and b, are not equal to zero.
Solution:
To check the numebr we need to find the vaules of
a1/a2, b1/b2, c1/c2
a1/a2 = -3/-6 = 1/2
b1/b2 = 4/8 = 1/2
c1/c2 = -5/-10 = 1/2
Since the values of a1/a2 = b1/b2 = c1/c2
Theerefore, the system of Linear Equation has Infinitely Many Solutions
To learn more about Linear Equation in Two Variables from the given link
https://brainly.com/question/24085666
#SPJ1
hello guys, can you give me the answers

Answers
The differentiation of the function y = sin(2 sin⁻¹x) is; dy/dx = d√(1 - y²)]/(√1 - x²)
How to differentiate functions?
1) We want to differentiate the function;
\(\frac{\sqrt{x + 1} + \sqrt{x - 1}}{\sqrt{x + 1} - \sqrt{x - 1} }\)
Differentiating this gives;
dy/dx = \(\frac{[(\frac{1}{2\sqrt{x + 1}} - \frac{1}{2\sqrt{x - 1}}) * \sqrt{x + 1} + \sqrt{x - 1}]}{(\sqrt{x + 1} - \sqrt{x - 1})^{2} }\)
That can be simplified to get;
dy/dx = \(\frac{\sqrt{x + 1} + \sqrt{x - 1} }{(x - 1)\sqrt{x + 1} + (-x - 1) \sqrt{x - 1}}\)
2) We want to differentiate the function;
y = sin(2 sin⁻¹x)
Differentiating the function gives;
dy/dx = [2cos(2 sin⁻¹x)]/√(1 - x²)
We know from trigonometric identity that;
cos²x = 1 - sin²x
Thus;
1 - sin²(2 sin⁻¹x) = cos²(2 sin⁻¹x)
But sin²(2 sin⁻¹x) = y²cos²(2 sin⁻¹x)
Thus; √(1 - y²) = cos(2 sin⁻¹x)
dy/dx = d√(1 - y²)]/(√1 - x²)
Read more about Differentiation of Functions at; https://brainly.com/question/5313449
#SPJ1
If the ratio of tourists to locals is 4:5 and there are 100 tourists at the opening of a new museum, how many locals are in attendance?
Answers
Answer:
125.
Given:
The ratio of the tourist to locals is 4:5There are 100 tourist at the opening.Step-by-step explanation:
As given in the question that the ratio is already given,
therefore,
1. The ratio of tourist of to locals
the ratio of tourist to local is 4:5
\(\frac{tourist}{locals}\)=\(\frac{4}{5}\)
2. Attendance of locals at the opening
here are 100 tourist at the opening
\(\frac{100}{locals} =\frac{4}{5}\)
locals= 125
locals are 125 in attendance.
https://brainly.com/question/16604112
#SPJ4
125 is the attendance of locals
In mathematics, ratios indicate the number of times one number contains another number. For example, if a fruit bowl contains 8 oranges and 6 lemons, the ratio of oranges to lemons is 8 to 6. Similarly, the ratio of lemons to oranges is 6:8 and the ratio of oranges to whole fruit is 8:14. A ratio number can be any kind of quantity, such as the number of people or things, or measurements such as length, weight, or time.In most situations, both numbers are constrained to be positive.
The ratio of tourists to locals is 4:5
Tourists / Locals = 4 / 5
There are 100 tourists at the opening of the new museum
100 / locals = 4/5
locals = 500/4
locals = 125
The attendance of locals is 125.
Learn more about ratio here
https://brainly.com/question/16604112
#SPJ4
find the value of A
75°,110°,90°
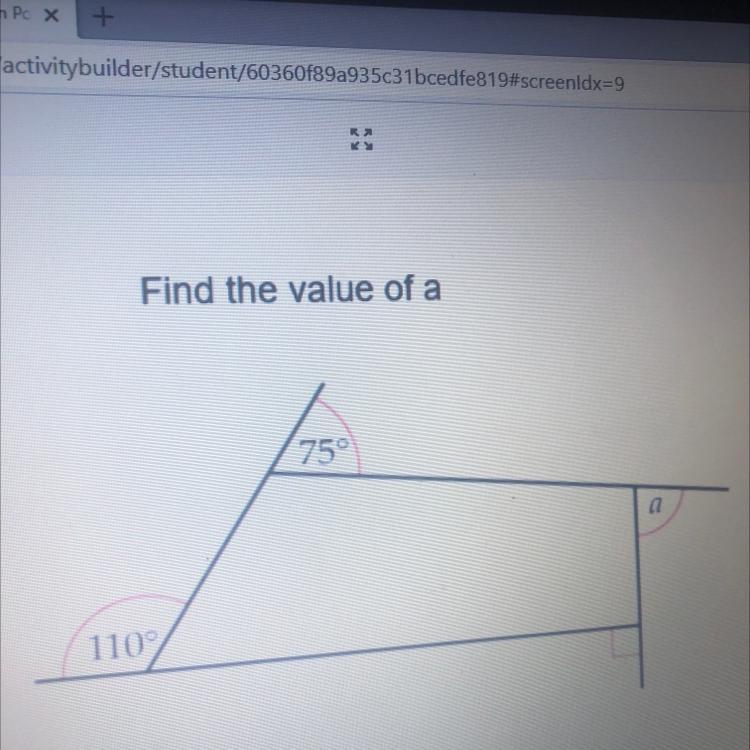
Answers
Answer:
I think it is 90° because on a line it is 180 and and both add up to 360°
Hope it helps
2. Solve for y
-4y -20 +19= -y + 17
i need someone to answer this it’s due by midnight
Answers
Answer:
y= -6
Step-by-step explanation:
A square pyramid has a base that is 4 inches wide and a slant height of 7 inches. What is the surface area, in square inches, of the pyramid?
Answers
The surface area is 72 square inches.
To find the surface area of a square pyramid, we need to calculate the area of the base and the four triangular faces.
Given that the base is 4 inches wide, the area of the square base is:
Base area = side² = 4² = 16 square inches.
The slant height is 7 inches. To find the area of one triangular face, we use:
Triangle area = (base * slant height) / 2
Each triangle has the same base length as the square base, which is 4 inches. Therefore, the area of one triangular face is:
Triangle area = (4 * 7) / 2 = 14 square inches.
Since there are four triangular faces, their total area is:
4 * Triangle area = 4 * 14 = 56 square inches.
Finally, add the base area and the total area of the triangular faces to get the surface area:
Surface area = Base area + Total triangular faces area = 16 + 56 = 72 square inches.
To learn more about triangle, refer below:
https://brainly.com/question/2773823
#SPJ11
What is operationalization of variable in research?
Answers
Operationalization of variables in research involves defining a concept in a way that it can be measured or observed.
It is the process of taking abstract concepts, such as attitudes, beliefs, or behaviors, and defining them in a way that they can be measured using empirical methods. This is done by creating a set of specific and concrete indicators or measures that represent the concept being studied. The operationalization of variables is a critical step in the research process, as it ensures that the data collected is both reliable and valid, and can be used to draw meaningful conclusions and make predictions.
Learn more about variables here: brainly.com/question/29583350
#SPJ4
PLEASE HELP
What type of line is the graph of 4x + y=-3?
1) Vertical
2) Horizontal
3) Rising
4) Falling
Answers
Answer: Falling
Step-by-step explanation:
Once you rearrange this equation into y-intercept form and you get y = -4x-3, you then graph the line and the line appears to be decreasing down.
A.Work out the most appropriate average for each data set.
a 6, 7, 5, 6, 9, 2, 6, 54
b 3.2, 5.4, 3.2, 3.2, 10.8, 4.5, 4.9
c TV, TV, DVD, film, TV, DVD
d 83, 79, 81, 83, 82
Answers
The mean or average of the dataset are calculated below by simply taking the average of each dataset.
What is mean of the data set?Mean of a dataset is the average of all the observations present in the table. It is the ratio of the sum of observations to the total number of elements present in the data set. The formula of mean is given by;
Mean = sum the data / total number data
a. 6, 7, 5, 6, 9, 2, 6, 54
The mean can be calculated as;
mean = 6 + 7 + 5 + 6 + 9 + 2 + 6 + 54 / 8
mean = 95/8 = 11.875
b. 3.2, 5.4, 3.2, 3.2, 3.2, 10.8, 4.5, 4.9
mean = 3.2 + 3.2 + 3.2 + 3.2 + 4.5 + 4.9 + 5.4 + 10.8 / 8
mean = 24/5 = 4.8
c. The data set given cannot have a mean
d. 83, 79, 81, 83, 82
mean = 79 + 81 + 82 + 83 + 83 / 5
mean = 408/5 = 81.6
Learn more on mean here;
https://brainly.com/question/1136789
#SPJ1
solve the following problems by writing a proportion. 8 is 40% of what number?
Answers
Let x be the number
40% of x = 8
\(\frac{40}{100}\times x=8\)\(\frac{40x}{100}=8\)Multiply both-side of the equation by 100
\(40x\text{ = 800}\)
Divide both-side of the equation by 40
\(x=20\)
Therefore, 8 is 40% of 20
Write the equation of a parabola that has a complex root at 4+5i and goes through the point (2,87)
Answers
Answer:not sure
Step-by-step explanation:
I have the same problem
A rectangular container with a square base, an open top, and a volume of 256 cm3 is to be made. What is the minimum surface area for the container
Answers
The minimum surface area of the container is: 96.00 cm² in the given case.
Let's call the length and width of the square base "x", and the height of the container "h". Since the container has a volume of 256 cm^3, we can write:
V = \(x^2 * h = 256\)
We want to minimize the surface area of the container, which consists of the area of the base plus the area of the four sides. The area of the base , and the area of each side is xh. Therefore, the total surface area of the container is:
A = \(x^2 + 4xh\)
We can solve for h in terms of x using the volume equation:
h = \(256 / (x^2)\)
Substituting this expression for h into the surface area equation, we get:
A(x) =
To find the minimum surface area, we need to find the critical points of the function A(x).
We can do this by taking the derivative of A(x) with respect to x, setting it equal to zero, and solving for x:
\(dA/dx = 2x - 1024 / x^2 = 0\\2x = 1024 / x^2\\x^3 = 512\\x = ∛512\\x ≈ 8.00 cm\)
To confirm that this is a minimum, we can check the second derivative:
\(d^2A/dx^2 = 2 + 2048 / x^3\)
This is positive, so A(x) has a minimum at x =\(∛512\). Therefore, the minimum surface area of the container is: 96.00 cm²
To learn more about surface area here
https://brainly.com/question/16519513
#SPJ4
How do you calculate the doubling time of a population?
Answers
The doubling time of a population can be computed by using the exponential growth formula: dt = ln(2)/r.
What is exponential growth?Exponential growth refers to a situation where the value keeps on increasing at a constant rate relative to the initial value.
The exponential growth function represents this situation and is given as
f(x) =a(1+r)ˣ
f(x) = exponential growth function
a = initial amount or value
r = growth rate
x = period of time
To find the population's doubling time, we can apply the exponential formula for time: dt = ln(2)/r
Where:
dt = the doubling time,
r = the growth rate (expressed as a decimal fraction)
ln(2) = the natural logarithm of 2 (about 0.693)
For instance, when a population has a growth rate of 0.05 (5%) per year, its doubling time is about ln(2)/0.05 = 13.9 years.
Thus, one can calculate the exact doubling time of a population by using the exponential growth equation above, solving for time.
Learn more about exponential growth equations at https://brainly.com/question/13223520.
#SPJ1
Answer:
We need to know the rate constant (k), which can be determined experimentally or given in the reaction's rate equation to calculate the half-life of a reaction or decay process.
Once you have the rate constant, you can use the following formula:
\(\bold{t_{\frac{1}{2}}=\frac{ln 2}{k}}\)
Where:
\(t_{\frac{1}{2}}\)
represents the half-life of the reaction or decay process.
ln represents the natural logarithm.
k is the rate constant.
By plugging in the appropriate rate constant into the formula, you can calculate the half-life for a specific chemical reaction or decay process.
Vertical angulation: Group of answer choices remains the same whether you are using the paralleling or the bisecting technique. is generally greater for images taken with the paralleling technique than it is for images taken with the bisecting technique. refers to the side-to-side plane. differs according to whether the paralleling or bisecting technique is being used.
Answers
Vertical angulation refers to the angle at which the x-ray beam is directed when taking dental radiographs. It is an important factor in obtaining clear and accurate images.
In both the paralleling and bisecting techniques, the group of answer choices remains the same. However, the vertical angulation is generally greater for images taken with the paralleling technique compared to the bisecting technique.
This is because the paralleling technique requires the x-ray beam to be directed more vertically in order to capture the entire tooth structure on the film. On the other hand, the bisecting technique involves angling the x-ray beam downward to intersect the imaginary bisector between the long axis of the tooth and the film.
Therefore, the vertical angulation differs depending on which technique is being used.
Know more about the Vertical angulation
https://brainly.com/question/1821791
#SPJ11
Point slope equation…help please

Answers
Answer:
using the formula
y -y1 = m(x -x1)
y -6 = 2(x -5)
y -6 = 2x -10
y = 2x -10+6
y =2x -4(equation of the line)
Rosea drives her car 30 kilometers to the train
station, where she boards a train to complete her trip. The
total trip is 120 kilometers. The average speed of the train is
20 kilometers per hour faster than that of the car. At what speed
must she drive her car if the total time for the trip is less than
2.5 hours?
Answers
Answer:
>34.88km/h
Step-by-step explanation:
Because we have two unknown values in this question (speed of train and speed of car), we will need two equations to solve it.
Firstly, we can make a big equation for time in terms of the vehicle speeds. Time = distance / speed, so if we use t for the train speed and c for the car speed, we get this equation for speed:
30/c + 90/t = 2.5
Here the 30 is the distance traveled by the car in km and the 90 is the distance traveled by the train in km (120 - 30 = 90).
We also know that the train speed was 20km/h faster than the car speed so our second equation is:
c + 20 = t
So now we can substitute this in the big equation so we only have one variable to solve for:
30/c + 90/(c+20) = 2.5
Now to solve this, this first step is to get rid of the fractions, which we can do by multiplying all the terms by the lowest common factor of the two denominators which is c(c+20):
(30/c)*c(c+20) + (90/c+20)*c(c+20) = 2.5
This simplifies to:
120c+600=2.5c^2+50c
and then into the quadratic equation:
2.5c^2-70c-600=0
This can be solved with the quadratic formula or a solver/calculator, and yields the solutions:
c=−6.88, 34.88 (both to 2dp)
We can eliminate the negative solution because speed cannot be negative meaning that Rosea must drive her car at the speed of at least/greater than 34.88km/h if she wants the total trip to be less than 2.5 hours.
Hope this helped!
hey! i’ll give brainliest thanks

Answers
Answer:
Iran
Step-by-step explanation:
HELP MATH NOT THE SMARTEST BIG SISTER!

Answers
Answer:
\(x=-20\)
Step-by-step explanation:
\(\frac{x}{5}+7=3\\ \\\frac{x}{5}+7-7=3-7\\ \\\frac{x}{5}=-4\\ \\\frac{x}{5}*5=-4*5\\ \\x=-20\)
Answer:
-20
Step-by-step explanation:
a=2x3^4x5 b=2^3x3^2x5^5 write down the night common factor of A and B PLEASE HELP ASAP PLEASEE!
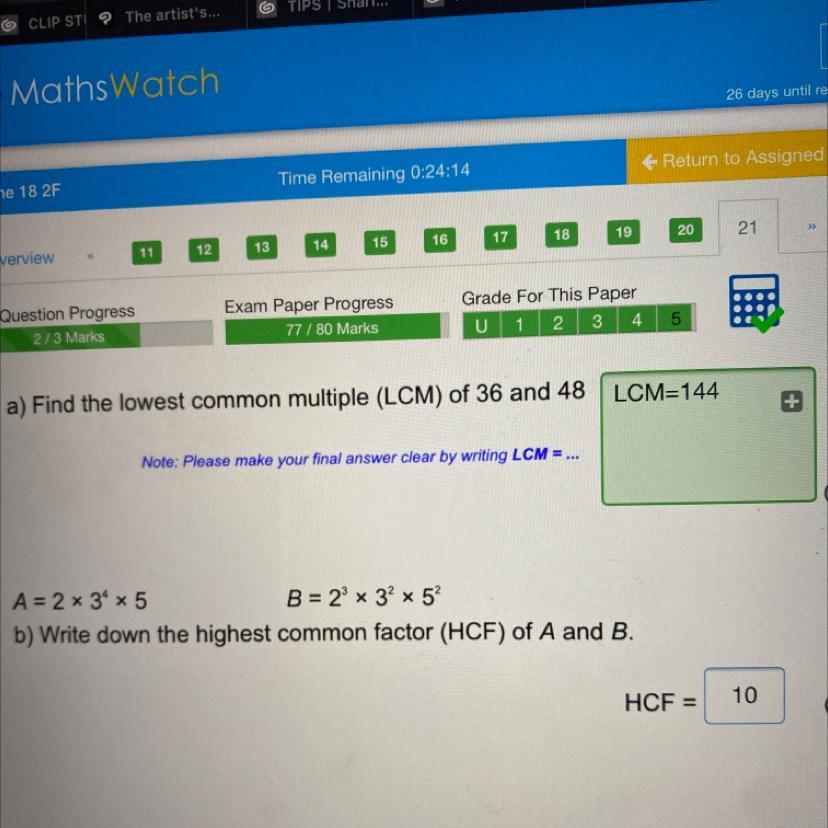
Answers
Answer:
The HCF of \(a=2^1 \cdot 3^4 \cdot 5^1\) and \(b = 2^3 \cdot 3^2 \cdot 5^2\) is \(90\).
Step-by-step explanation:
To calculate the HCF of two numbers given their prime factorization, we take the lowest exponent of every prime when comparing the two numbers.
So the HCF of \(a=2^1 \cdot 3^4 \cdot 5^1\) and \(b = 2^3 \cdot 3^2 \cdot 5^2\) is \(2^1 \cdot 3^2 \cdot 5^1 = 90\).
9. Maxima Motors is a French-owned company that produces automobiles and all of its automobiles are produced in United States plants. In 2014, Maxima Motors produced $32 million worth of automobiles, with $17 million in sales to Americans, $11 million in sales to Canadians, and $4 million worth of automobiles added to Maxima Motors’ inventory. The transactions just described contribute how much to U.S. GDP for 2014?
A. $15 million
B. $17 million
C. $21 million
D. $28 million
E. $32 million
Answers
The answer is , the transactions just described contribute how much to U.S. GDP for 2014 is $17 million. Option (b) .
Explanation: Gross domestic product (GDP) is a measure of a country's economic output.
The total market value of all final goods and services produced within a country during a certain period is known as GDP.
The transactions just described contribute $17 million to U.S. GDP for 2014. GDP is made up of three parts: government spending, personal consumption, and business investment, and net exports.
The transactions just described contribute how much to U.S. GDP for 2014 is $17 million.
To know more about Investment visit:
https://brainly.com/question/30105963
#SPJ11
u=xy/5, solve for x
i’m so confused???
Answers
u=yx/5
2. Multiply both side by 5/y
5u/y=x
3. Then y write it in parametric form
X=5u/y
????????????????????

Answers
Answer:
|7| = 7
|-7| = 7
Step-by-step explanation:
Each is 7 numbers away from zero.
Absolute value is always positive.
Find the value of A) 3/5 multiplied by - 2/7, B) - 1/5+-1/3
Answers
A. -2/7
B. -8/15
hope it helps...!!!
