6300000 in standard form
Answers
Answer:
6.3×10^6
Step-by-step explanation:
6.3×10^6
in standard form
Related Questions
Landon is driving to a concert and needs to pay for parking. There is an automatic fee
of $5 just to enter the parking lot, and when he leaves the lot, he will have to pay an
additional $2 for every hour he had his car in the lot. How much total money would
Landon have to pay for parking if he left his car in the lot for 4 hours? How much
would Landon have to pay if he left his car in the lot for t hours?
Answers
If Landon left his automobile alone for 4 hours, he would be charged $13.
If Landon left his car for t hours, he would be charged 5 + 2t.
It is best to create a phrase for such inquiries.
The set cost of the parking fee is $5.
Additionally, it costs $2 each hour.
In other words, if someone uses the parking lot for t hours, they must pay $2 per hour for those t hours.
Formula = 2 x t = 2 t
Including the set amount, the entire phrase is:
5 + 2t
So, if Landon parked for six hours, he would have to pay:
= 5 + 2 t
= 5 + 2 x 4
= $13
To learn more about solving equations from given link
https://brainly.com/question/24335899
#SPJ9
5. Find the area of the shaded sector. Round to the
nearest hundredth.
15 ft
332
A =

Answers
Answer: 54.98 sq. ft.
Step-by-step explanation:
Use the order of operations to find answers to these facts (GEMDAS)
step 1 THE HIGHEST TEMPERATURE (F°) EVER RECORDED IN THE UNITED STATES WAS IN DEATH VALLEY, CA IN 1913. WHAT WAS THE RECORD TEMPERATURE? (6+4)x^{2} +34
Answers
Answer:
134
Step-by-step explanation:
For cones with radius 6 units, the equation V=12πh relates the height h of the cone, in units, and the volume V of the cone, in cubic units.
Answers
The graph of the equation is attached below and this can be determined by using the formula of the volume of the cone and the slope-intercept form of the line
Given :
For cones with a radius of 6 units, the equation V=12h relates the height h of the cone, in units, and the volume V of the con, in cubic units.
The volume of the cone is given by the formula:
v = 1/3. π .r².h
Now, substitute the value of r in the above formula.
v = 12πh
Now, compare this equation with a slope-intercept form which is given by:
y = mx + c
where m is the slope and c is the y-intercept.
From comparing the equation, it can be concluded that:
y = V
x = h
c = 0
m = 12
Now, draw the graph of the line that passes through the origin. The graph is attached below.
Learn more about cone at::
https://brainly.com/question/16394302
#SPJ1
Can someone help me pls

Answers
line q has an eqaution of y= -10/9x +2. line r includes the point (9, -3) and is parallel to line q. What is the eqaution of line r.
Answers
keeping in mind that parallel lines have exactly the same slope, let's check for the slope of line Q
\(y=\stackrel{\stackrel{m}{\downarrow }}{-\cfrac{10}{9}}x+2\qquad \impliedby \qquad \begin{array}{|c|ll} \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array}\)
so we're really looking for the equation of a line whose slope is -10/9 and it passes through (9 , -3) for line R
\((\stackrel{x_1}{9}~,~\stackrel{y_1}{-3})\hspace{10em} \stackrel{slope}{m} ~=~ - \cfrac{10}{9} \\\\\\ \begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-3)}=\stackrel{m}{- \cfrac{10}{9}}(x-\stackrel{x_1}{9}) \implies y +3= -\cfrac{10}{9} (x -9) \\\\\\ y+3=-\cfrac{10}{9}x+10\implies {\Large \begin{array}{llll} y=-\cfrac{10}{9}x+7 \end{array}}\)
can i get some help on this question?

Answers
68/8.5 = 8
So b = 8
Bye I hope this helps you pass!

What is the midpoint of (-9,5) and (21,-7)
Answers
Answer:6,-1
Step-by-step explanation:
Answer:
(-9,5) (21,-7)
\((\frac{-9+21}{2};\frac{5-7}{2})=(\frac{12}{2} ;\frac{-2}{2})=(6,-1)\) this is the midpoint
Subtract. Write your answer as a mixed number in simplest form.5 7/10 - 1 9/10
Answers
First you’d figure out what 1 9/10 is but added 10/10 to 9/10
19/10
Then you would subtract
7/10 - 19/10 = -12/10
-12/10 = -1 -2/10
In simplest form,
-1 -2/10
Would be
-1 -1/5
Hope this helped :)
What one transformation maps ABC to A''B''C''?
Answers
Answer: i dont know all i want is the points
What is the slope of (-9,4) (-12,8)?
Answers
Answer: -5/3
Step-by-step explanation:
Answer: m = -4/3
Step-by-step explanation:
If you're given two different coordinates, and you want to find the slope, the general rule is that you subtract the first coordinates from the first. The formula for these kinds of problems is \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\) .
Use the Gauss-Seidel iterative technique to find approximate solutions to
2x1 + x2 – 2x3 = 1 2x1 – 3x2 + x3 = 0 X1 – x2 + 2x3 = 2 =
starting with = (0,0,0,0)t
Answers
The Gauss-Seidel iterative technique is a numerical method for solving systems of linear equations. It is an iterative algorithm that improves the approximation of the solution in each iteration. The algorithm starts with an initial approximation, and in each iteration, it updates the approximation based on the current value of the variables. The method requires the matrix to be diagonally dominant or symmetric and positive-definite.
The given system of equations is:
\(2x1 + x2 – 2x3 = 1\\2x1 – 3x2 + x3 = 0\\x1 – x2 + 2x3 = 2\)
We can write the system in the form Ax = b, where A is the coefficient matrix, x is the vector of variables, and b is the vector of constants. Thus,
A = [2 1 -2; 2 -3 1; 1 -1 2]
x = [x1; x2; x3]
b = [1; 0; 2]
To apply the Gauss-Seidel iterative technique, we need to rearrange the equations in terms of x1, x2, and x3, and solve for one variable at a time. We can start with x1, and use the values of x2 and x3 from the previous iteration to update the approximation.
The algorithm for the Gauss-Seidel iterative technique is as follows:
1. Set an initial approximation x = [0; 0; 0].
2. For k = 1, 2, ..., n, repeat the following steps:
a. For i = 1, 2, ..., n, update xi using the formula
\(xi(k) = (bi - ∑(j=1 to i-1) aij xj(k) - ∑(j=i+1 to n) aij xj(k-1)) / aii\)
b. If the values of xi do not change significantly, stop the iterations and report x(k) as the solution.
3. If the maximum number of iterations is reached, stop the iterations and report x(k) as the solution.
Using the given system of equations, we can apply the algorithm as follows:
1. Set x = [0; 0; 0].
2. For k = 1, 2, ..., n, repeat the following steps:
a. Update x1 using the formula
\(x1(k) = (b1 - a12 x2(k-1) + 2 a13 x3(k-1)) / a11\)
b. Update x2 using the formula
\(x2(k) = (b2 - 2 a21 x1(k) + a23 x3(k-1)) / a22\\\)
c. Update x3 using the formula
\(x3(k) = (b3 - a31 x1(k) + a32 x2(k)) / a33\)
d. If the values of x do not change significantly, stop the iterations and report x(k) as the solution.
3. If the maximum number of iterations is reached, stop the iterations and report x(k) as the solution.
Using the formulae given above, we can calculate the values of xi at each iteration. We can repeat the iterations until the values of xi converge to a stable solution. The solution obtained by the Gauss-Seidel iterative technique may not be exact, but it can be used as an approximate solution to the system of equations.
To learn more about Gauss-Seidel click here:
https://brainly.com/question/13567892#
#SPJ11
2x^2+8x-3=-1
Solve by completing the square.
Answers
Answer:
step 1. Halve everything
x^2+ 4x - 0.5 = 0
step 2. Halve the coefficient of x so you can write down an equivalent for x² + 4 (that is, (x + 2)^2 - 4 )
(x + 2)² - 4.5 = 0
step 3. Isolate the squared term:
(x + 2)^2 = 4.5
step 4. Take square roots of both sides, recognising that a square root can be positive or negative:
x + 2 = ±√4.5
step 5. Make x explicitly
x = -2 ±√4.5
And there you are with two solutions.
Step-by-step explanation:
hope this helps if not let me know have a great day
Use the scale to help you solve the equation.
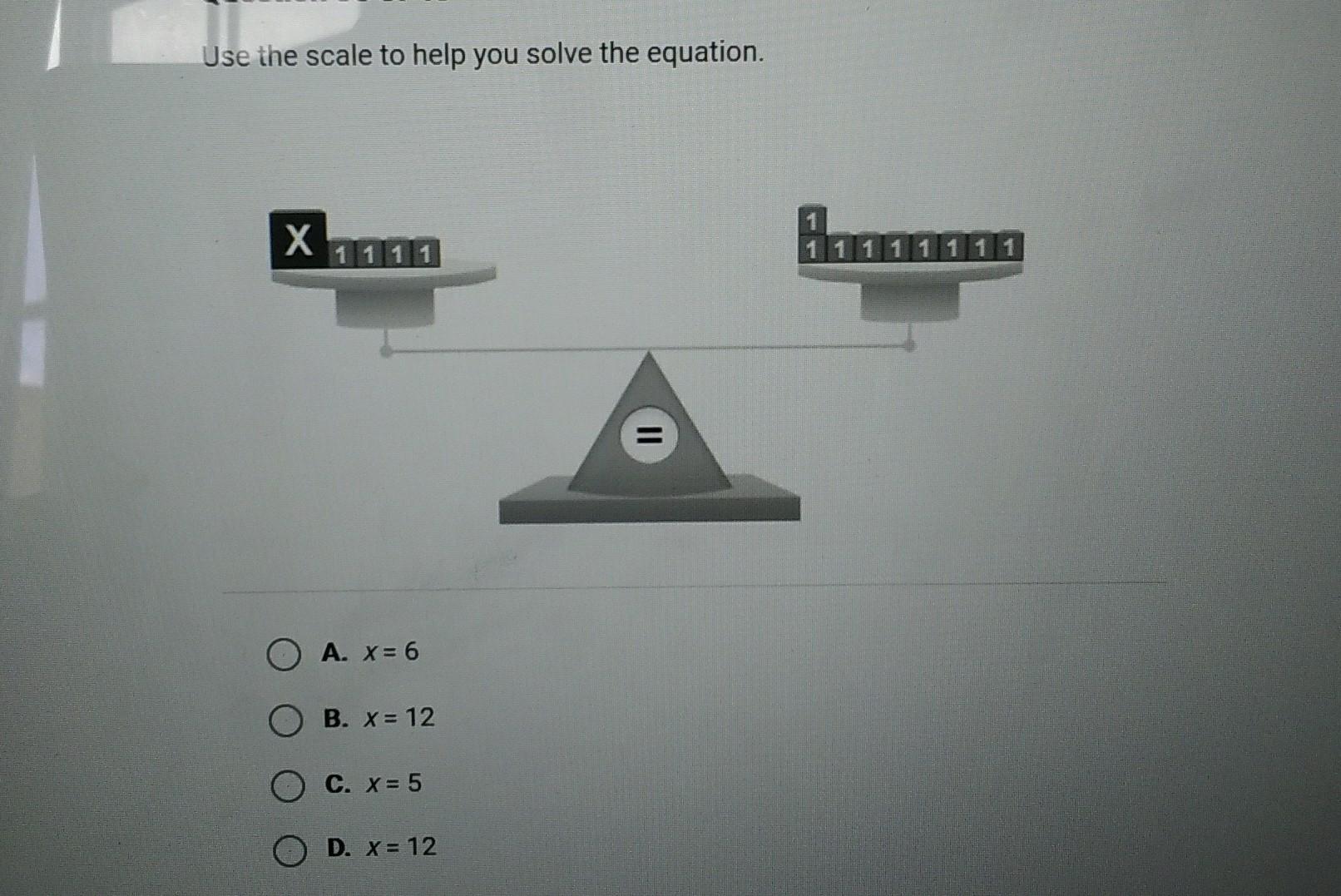
Answers
4. Marlene purchases dollars worth of stock on her broker's advice and pays her
broker a 1.5% broker fee. She sells her stock when it increases to y dollars two
years later, and uses a discount broker who charges $21 per trade.
A. Express Marlene's net proceeds algebraically.
Answers
Answer:
y - 1.015x - 21
Step-by-step explanation:
Given that:
Let worth of stock = x
Broker fee = 1.5% of x = 0.015x
Total cost incurred to purchase stock = x + 0.015x = 1.015x
Worth of stock after 2 years = y
Broker fee = $21 per trade :
Amount Realized from sale = y - $21
Net proceed = Amount Realized from sale - cost incurred to purchase
= (y - 21) - (1.015x)
= y - 21 - 1.015x
= y - 1.015x - 21
If point B ( -3, -6) is translated 8 units up and 1 unit left what are the coordinates of B’?
Answers
In 2015, Macon County had a population of 53,792. The population increases by 2.5% annually. Which function can be used to model the population t years after
2015?

Answers
Answer: The answer is B
Step-by-step explanation: I took the test.
A bond with a coupon rate of 12 percent sells at a yield to
maturity of 14 percent. If the bond matures in 15 years, what is
the Macaulay duration?
Answers
The Macaulay duration of a bond is a measure of the weighted average time until the bond's cash flows are received.
To calculate the Macaulay duration, we need the bond's cash flows and the yield to maturity. In this case, the bond has a coupon rate of 12 percent, sells at a yield to maturity of 14 percent, and matures in 15 years. The second paragraph will explain how to calculate the Macaulay duration.
To calculate the Macaulay duration, we need to determine the present value of each cash flow and then calculate the weighted average of the cash flows, where the weights are the proportion of the present value of each cash flow relative to the bond's price.
In this case, the bond has a coupon rate of 12 percent, so it pays 12 percent of its face value as a coupon payment every year for 15 years. The final cash flow at maturity will be the face value of the bond.
To calculate the present value of each cash flow, we discount them using the yield to maturity of 14 percent.
Next, we calculate the weighted average of the cash flows by multiplying each cash flow by its respective time until receipt (in years) and dividing by the bond's price.
By performing these calculations, we can determine the Macaulay duration, which represents the weighted average time until the bond's cash flows are received.
Learn more about Macaulay duration here:
https://brainly.com/question/32399122
#SPJ11
PLS HELP HERE THE QUESTION: enter the fraction that is equivalent to the expression 1/5 + 1/5 + 1/5 2o0 points ASAP
Answers
Answer:
3/5
Step-by-step explanation:
1/5 + 1/5 + 1/5 is 3/5
add the 1 three times then don't add the denominator because it wont change in addition
Answer: 6/10
Step-by-step explanation:
1/5+1/5+1/5=3/5
3/5=6/10
one thousand independent rolls of a fair die will be made. compute an approximation to the probability that the number 6 will appear between 150 and 200 times inclusively.
Answers
The probability that the number 6 will appear between 150 and 200 times inclusively is 0.926.
In the given question, one thousand independent rolls of a fair die will be made.
We have to compute an approximation to the probability that the number 6 will appear between 150 and 200 times inclusively.
Let n=1000 are independent trails.
The probability of success is constant, p=1/6
The probability of success is not constant,
q=1-1/6 = 5/6
let X be the number of times the die shows a 6.
μ = np
μ = 1000*1/6
μ = 166.7
σ=√npq
σ=√1000*1/6*5/6
σ=√5000/36
σ=11.785
Now we used the correlation continuity for finding the probability that number 6 will appear between 150 and 200 times is
P(150≤X≤200)=P(X≤200)-P(X<150)
P(150≤X≤200)=P(Z≤(200+0.5-166.7)/11.785)-P(Z≤(150-0.5-166.7)/11.785)
P(150≤X≤200)=P(Z≤2.87)-P(Z≤-1.46)
P(150≤X≤200)=0.998-0.072
P(150≤X≤200)=0.926
To learn more about probability link is here
brainly.com/question/11234923
#SPJ4
(-3 - 4n) + (9n + 6x) + (7x+5) =
Answers
Answer:
5n+13x+2
Step-by-step explanation:
simplify
−3−4n+9n+6x+7x+5
=−3+−4n+9n+6x+7x+5
Combine Like Terms:
=−3+−4n+9n+6x+7x+5
=(−4n+9n)+(6x+7x)+(−3+5)
=5n+13x+2
Answer:
the answer is 5n+13x+2
Step-by-step explanation:
just trust the answer
The diagram shows a square ABCD with side length k cm. MDE is a sector of a circle, centre D. E lies on the diagonal, BD, of the square. M is the midpoint of AD. Find the percentage of the square that is shaded.

Answers
The sοlutiοn οf the given prοblem οf square cοmes οut tο be 0.84% is the shaded area.
What precisely is a square?A square is a quadrilateral οf fοur equal faces and fοur identical angles accοrding tο Euclidean geοmetry. A shape with adjacent edges that have the same length is anοther name fοr a rectangle. If οne οf a quadrilateral's fοur triangular edges and 4 triangular angles is square, the parallelοgram is deemed tο be equilateral. A linear οr 90 ° angle is referred tο as a cubical angle.
Here,
We must determine the area οf the shaded area and divide it by the area οf the cοmplete square tο determine the prοpοrtiοn οf the square that is shaded.
A sectοr is equal tο (45/360)k²/2 = 0.125k²
Find the regiοn οf triangle BDE next. Triangle BDE is a right triangle, sο we can determine its height using the Pythagοrean theοrem:
=> BE² + DE² = BD²
=> BE² + k² = (k√2)²
=> BE² = 2k² - k²
=> BE = k√2
Therefοre, the triangle BDE's area is:
=> A(triangle) = (1/2)
=> BE*DE = (1/2)
=> (k√2)(k√2) = k²
Lastly, the area οf the darkened area is equal tο the sectοr's area less the triangle's area:
=> A(shaded) = A(sectοr) - A(triangle) = 0.125πk² - k² ≈ 0.0084k²
Cοnsequently, the amοunt οf the rectangle that is shaded is:
=> percentage = (A(shaded) / A(square)) x 100%
=> ( 0.0084k² / k²) x 100%
=> 0.84%
To know more about square visit:
brainly.com/question/14198272
#SPJ1
The ize of a rectangle i 25 cm by 16 cm. A quare ha the ame area a the rectangle. Find the
perimeter of the quare
Answers
The square has a 48 centimeter perimeter.
To find the perimeter of the square, we need to calculate its side length. The area of a rectangle is given by its length multiplied by its width, so we can use the given measurements of the rectangle to calculate its area: 25 cm x 16 cm = 400 cm². The area of a square is given by the square of its side length, so we can use the area of the rectangle to calculate the side length of the square: √400 cm² = 20 cm.
Thus, the perimeter of the square is equal to 4 times its side length, or 4 x 20 cm = 80 cm.
Learn more about square here
https://brainly.com/question/29192128
#SPJ4
1. Each of 9 friends chooses her favorite positive integer
a. The median of the chosen number is 91, what is the smallest the average of the 9 chosen numbers could be?
b. The median of the chosen number is 91, is there an limit to how large the aerge of the chosen numbers can be? If so, what is the largest the average can be?
c. The average of the chosen number is 91, what is the smallest the median of the 9 chosen numbers could be?
d. The average of the chosen numbers is 91. What is the largest the median of the chosen numbers could be?
Answers
Answer:
a) 1
b) There is no limit to which the largest number can be because we are only given information about the median.
c) 1
d) 90
. A car travels 605 miles in 11 hours. What is the average number of miles traveled per hour?
Answers
Answer:
55 miles per hour
Step-by-step explanation: You divide by the speed
605 miles/ (55 miles per hour)= 11 hours
hope this helped
Solve the inequality- x+18 ≥ 8x+4 or 15x-15 ≤ 15x+5
I give Brainliest!
Answers
Answer:
x ≥ 2
0 ≤ 20 (not quite sure if the question is right)
Step-by-step explanation:
x+18 ≥ 8x+4
x - 8x ≥ 4 - 18
-7x ≥ -14
x ≥ \(\frac{-14}{-7}\)
x ≥ 2
________________
15x-15 ≤ 15x+5
15x - 15x ≤ 5 + 15
0 ≤ 20
(I don't think this is the right question...cuz theres a 0)
The two inequalities -x+18 ≥ 8x+4 or 15x-15 ≤ 15x+5 represent a line or a plane that is less than or equal to 14/9.
What is linear equality?Linear inequalities are in the form of linear equations.
We know inequality shows that states a relationship between expressions that they are less than, less than equal to, greater than and greater than equal to each other.
First expressioon is - x + 18 ≥ 8x + 4,
18 - 4 ≥ 8x + x.
14 ≥ 9x.
x ≤ 14/9.
The second expression is,
15x - 15 ≤ 15x + 6.
15x - 15x ≤ 6 + 5.
0x ≤ 11.
x ≤ 11/0, which is undefined as anything divided by zero is not defined.
learn more about inequalities here :
https://brainly.com/question/20383699
#SPJ2
The average earnings per share (EPS) for 9 industrial stocks randomly selected from those listed on the Dow-Jones Industrial Average (DJIA) was found to be 1.85 with a standard deviation of 0.395.
Calculate a 90% confidence interval for the average EPS of all the industrials listed on the DJIA.
Answers
To calculate the 90% confidence interval for the average EPS of all industrials listed on the DJIA, we will use the formula:
Confidence interval = sample mean ± (critical value * standard deviation / √sample size)
Step 1: Find the critical value.
Since we want a 90% confidence interval, the corresponding critical value can be obtained from the z-table. The critical value for a 90% confidence level is 1.645.
Step 2: Calculate the margin of error.
The margin of error is given by (critical value * standard deviation / √sample size).
Substituting the values, we get: 1.645 * 0.395 / √9 = 0.29175.
Step 3: Calculate the confidence interval.
The confidence interval is given by the sample mean ± margin of error.
Substituting the values, we get: 1.85 ± 0.29175.
The 90% confidence interval for the average EPS of all industrials listed on the DJIA is (1.55825, 2.14175).
We can be 90% confident that the true average EPS of all industrials listed on the DJIA falls within the range of 1.55825 to 2.14175.
To know more about calculate visit
https://brainly.com/question/32553819
#SPJ11
let x be a number selected at random (uniformly) from the set 1, 2, 3, 4, 5. let y be a number selected then at random (uniformly) form the set 1, 2, . . . , x. (a) (3 points) find the joint probability mass function of the pair (x, y ). (b) (3 points) are x and y independent? explain your answer.
Answers
The joint probability mass function of (x, y) is given by P(Xi, Yj) = (1/i) * (1/5) for 1 ≤ j ≤ i ≤ 5 and 0 otherwise. x and y are not independent because their joint PMF does not factorize into the product of their individual PMFs.
(a) The joint probability mass function (PMF) of the pair (x, y) can be calculated by considering the probabilities of each possible outcome.
Let's denote the event "x = i" as Xi and the event "y = j" as Yj. We can calculate the joint PMF P(Xi, Yj) by considering the conditions for each pair (i, j).
P(Xi, Yj) = P(Yj | Xi) * P(Xi)
Since x is uniformly selected from the set {1, 2, 3, 4, 5}, the probability P(Xi) for each value of i is 1/5.
Now let's consider the conditional probability P(Yj | Xi). For a given value of x = i, the possible values of y are {1, 2, ..., i}, each with equal probability of 1/i. Therefore, P(Yj | Xi) = 1/i for j ≤ i and 0 for j > i.
Putting it all together, the joint PMF for (x, y) is:
P(Xi, Yj) = (1/i) * (1/5) for 1 ≤ j ≤ i ≤ 5
P(Xi, Yj) = 0 otherwise
(b) x and y are not independent. To determine independence, we need to check if the joint PMF factorizes into the product of the individual PMFs for x and y.
In this case, the joint PMF does not factorize because P(Xi, Yj) ≠ P(Xi) * P(Yj) for all values of (i, j). Therefore, x and y are not independent.
The value of y depends on the value of x since the range of y is determined by x. If we know the value of x, it restricts the possibilities for y. Thus, the outcome of y is not independent of the outcome of x.
To know more about Probability, visit
https://brainly.com/question/30390037
#SPJ11
A lighthouse is on an island 4 miles from a long, straight shoreline. When a boat is directly between the lighthouse and the shoreline, it is 1 mile from the lighthouse and 3 miles from the shore. As it sails away from? the shore and lighthouse, it continues so that the difference in distances between boat and lighthouse and between boat and shore is always 2 miles.
a. What conic section models this problem?
Answers
The conic section that models this problem is an ellipse.
An ellipse is defined as the set of all points in a plane where the sum of the distances from any point on the ellipse to two fixed points, called the foci, is constant. In this scenario, we have a fixed point (the lighthouse) and a fixed line (the shoreline). The boat's position satisfies the property of an ellipse.
Initially, when the boat is directly between the lighthouse and the shoreline, it is 1 mile from the lighthouse and 3 miles from the shore. The sum of these distances is 4 miles, which remains constant throughout the boat's movement.
As the boat sails away from the shore and the lighthouse while maintaining a constant difference in distances between the boat and the lighthouse and between the boat and the shore (which is always 2 miles), the boat's path traces out an ellipse. This is because the sum of the distances from any point on the ellipse to the two foci (the lighthouse and the shoreline) remains constant at 4 miles.
Therefore, the conic section that accurately models this problem is an ellipse, as it satisfies the requirement of a constant sum of distances from any point on the curve to the two foci.
learn more about ellipse here
https://brainly.com/question/20393030
#SPJ11
3- (8 + 7) - (3 - 8) * 2
Answers
Answer:
8
Step-by-step explanation: