.5. Suppose that X has a gamma distribution with parameters α and β.
(a) If k is a constant satisfying α + k > 0, show that E[X^k] = β^kΓ(α + k) / Γ(α) .
What does this reduce to when k = 1?
(b) If Y has a χ2 distribution with ν degrees of freedom, what is E[Y^a]?
Answers
a. When k = 1, E[X] reduces to the parameter β of the gamma distribution.
b. If Y has a χ2 distribution with ν degrees of freedom, E[Y^a] = (ν/2)^a * Γ(ν/2 + a) / Γ(ν/2)
(a) To show that E[X^k] = β^k * Γ(α + k) / Γ(α), where X has a gamma distribution with parameters α and β, and α + k > 0, we can use the moment-generating function (MGF) of the gamma distribution.
The MGF of a gamma distribution with parameters α and β is given by:
M(t) = (1 - βt)^(-α)
To find E[X^k], we differentiate the MGF with respect to t, k times, and evaluate it at t = 0.
d^k/dt^k [M(t)]|t=0 = d^k/dt^k [(1 - βt)^(-α)]|t=0
By applying the kth derivative rule and simplifying, we obtain:
E[X^k] = β^k * Γ(α + k) / Γ(α)
This is the desired result.
When k = 1, the equation becomes:
E[X] = β^1 * Γ(α + 1) / Γ(α)
Simplifying further, we have:
E[X] = β * αΓ(α) / Γ(α) = β
So, when k = 1, E[X] reduces to the parameter β of the gamma distribution.
(b) If Y has a χ2 distribution with ν degrees of freedom, the expected value of Y^a can be found using the moment-generating function (MGF) of the chi-square distribution.
The MGF of a chi-square distribution with ν degrees of freedom is given by:
M(t) = (1 - 2t)^(-ν/2)
To find E[Y^a], we differentiate the MGF with respect to t, a times, and evaluate it at t = 0.
d^a/dt^a [M(t)]|t=0 = d^a/dt^a [(1 - 2t)^(-ν/2)]|t=0
By applying the ath derivative rule and simplifying, we obtain:
E[Y^a] = (ν/2)^a * Γ(ν/2 + a) / Γ(ν/2)
This is the desired result for E[Y^a] when Y has a chi-square distribution with ν degrees of freedom.
Learn more about gamma distribution at
https://brainly.com/question/31055660
#SPJ11
Related Questions
HELPPP ASAP!!! WILL GIVE BRAINLYIST!!

Answers
Answer: The reflection is across x = 6.
Step-by-step explanation:
As you look at the reflection, you can see there is a shadowing with the two points on this graph. Point X1 is on (6, -1) and Point X is on (6, -7)
When looking at the graph, you can easily eliminate the x-axis and y-axis for an answer is because neither Point X1 nor Point X has a relationship to the axis.
Since the coordinates are precisely 6 units from each other, there is a reflection across x = 6.
Therefore, the reflection is across x = 6. Hope this helps!
-From a 5th Grade Honors Student
I NEED HELP THIS IS DUE BY THE END OF THE DAY AND ITS 3:03 PLEASE HELPPP
find the equation of the line that passes through ( -2,8) and (5,6)
Answers
Answer: the equation is
y=-2/7x +52/7 and the slope is -2/7
Step-by-step explanation:
How do you solve (x+3)^2=121? Sorry it's been a while...
Answers
Answer: x = 8
Step-by-step explanation:
(x + 3)^2 = 121
Take the square root of both sides
x + 3 = 11
x = 8
Plug it back in to double check
(8 + 3)^2 = 121
(11)^2 = 121
121 = 121
The algebraic expression 6x² + 9x + 3 represents the area of a rectangle. What is the area of the
rectangle when x = 3 feet?
a. 51 square feet
b. 60 square feet
c. 66 square feet
d. 84 square feet

Answers
Which system of linear equations has only one solution? Why? How about the system of linear equations with no solution? Infinite number of solutions? Explain your answer.
Answers
The system of linear equations which has the rank of coefficient matrix equal to augmented matrix and equal to the number of unknowns, has only one solution called the unique solution.
Two types of system of equations exist- consistent and inconsistent.
Inconsistent means that it has no solution , i.e. the solution does not exist , here
Rank of augmented matrix is not equal to that of coefficient matrix.
Consistent system means a solution of the equation exists i.e.
rank of augmented matrix = rank of coefficient matrix.
Now, a consistent system can be of two types again - It may have a unique solution ,i.e.
rank of augmented matrix = rank of coefficient matrix = no. of unknowns
or an infinite number of solutions, where
rank of augmented matrix = rank of coefficient matrix < no. of unknowns (here we need to assign an arbitrary value to a free variable to find its solutions).
For e.g. let us consider the system -
x + y+ z = 0
2x + 3y + 4z = 1
Since , (0,0,0) is obviously satisfying the equation and so is a solution to this system , the given system is a consistent system .
Also, for a system to be consistent , either a unique solution exists or an infinite number of solutions exist. There is no particular number of solutions.
Here, we see that (-1,1,0) is also a solution other than the zero solution.
We can clearly see that the number of unknown variables , x,y,z is 3 and the number of equations is 2.
Thus, The system if there are fewer equations than variables has infinite solutions, equal number of equations as the unknowns has the unique solution.
To learn more about system of equations, visit link - brainly.com/question/13997560
#SPJ4
pls help asap if you can!!!!!

Answers
Answer:
x = 24
Step-by-step explanation:
if a and b are parallel then
62 and 5x - 2 are same- side interior angles and sum to 180° , that is
5x - 2 + 62 = 180
5x + 60 = 180 ( subtract 60 from both sides )
5x = 120 ( divide both sides by 5 )
x = 24
thus for a to be parallel to b , then x = 24
If z = 2x2 - 3y with u = x2 siny and v= 2y cosx, determine expressions for dz/du and dz/dv
Answers
The expressions for dz/du and dz/dv are as follows:
dz/du = 4x siny
dz/dv = -6y cosx
To find the expressions for dz/du and dz/dv, we need to differentiate the given function z = 2x^2 - 3y with respect to u and v, respectively.
1. dz/du:
Since u = x^2 siny, we can express z in terms of u by substituting x^2 siny for u in the original function:
z = 2u - 3y
Now, we differentiate z with respect to u while treating y as a constant:
dz/du = d/dx (2u - 3y)
= 2(d/dx (x^2 siny)) - 0 (since y is constant)
= 2(2x siny)
= 4x siny
Therefore, dz/du = 4x siny.
2. dz/dv:
Similarly, we express z in terms of v by substituting 2y cosx for v in the original function:
z = 2x^2 - 3v
Now, we differentiate z with respect to v while treating x as a constant:
dz/dv = d/dy (2x^2 - 3v)
= 0 (since x^2 is constant) - 3(d/dy (2y cosx))
= -6y cosx
Therefore, dz/dv = -6y cosx.
In summary, the expressions for dz/du and dz/dv are dz/du = 4x siny and dz/dv = -6y cosx, respectively.
To learn more about expressions, click here: brainly.com/question/4344214
#SPJ11
Find the value of x.

Answers
Answer: 33
Step-by-step explanation:
Hii can someone please help me with this question I prize you brianliest

Answers
Evaluating the relation, we can see that in the step 6 there are 35 squares.
What would be the number of squares in step 6?Here we have the relation:
h(n) = n² - 1
Where h(n) is the number of squares at the step number n.
Here we want to find the number of squares at the step 6, then to find this, we just need to replace n by the number 6.
We will get:
h(6) = 6² - 1
h(6) = 36 - 1
h(6) = 35
So we can see that in the step 6 there are 35 squares.
Learn more about evaluating relations at:
https://brainly.com/question/4344214
#SPJ1
Calculate the 95% confidence interval for the following fictional data regarding daily TV viewing habits: µ= 4.7 hours; σ= 1.3 hours; sample of 78 people, with a mean of 4.1 hours.
Answers
We can be 95% confident that the true population mean TV viewing time is between 3.812 and 4.388 hours.
To calculate the 95% confidence interval, we use the formula:
CI = x' ± Zα/2 * (σ/√n)
Where:
x' = sample mean
Zα/2 = the Z-score associated with the desired confidence level (in this case, 95%, so Zα/2 = 1.96)
σ = population standard deviation
n = sample size
Substituting the given values, we get:
CI = 4.1 ± 1.96 * (1.3/√78)
Calculating the standard error (SE) first:
SE = σ/√n
SE = 1.3/√78
SE ≈ 0.147
Then we substitute the SE value in the CI formula:
CI = 4.1 ± 1.96 * 0.147
CI = 4.1 ± 0.288
CI = (3.812, 4.388)
To learn more about confidence interval click on,
https://brainly.com/question/13956031
#SPJ4
Find the distance between the points (7, -4) and (7,5).
Answers
Answer:
9
Step-by-step explanation:
find absolute value
What is the answer to this question?
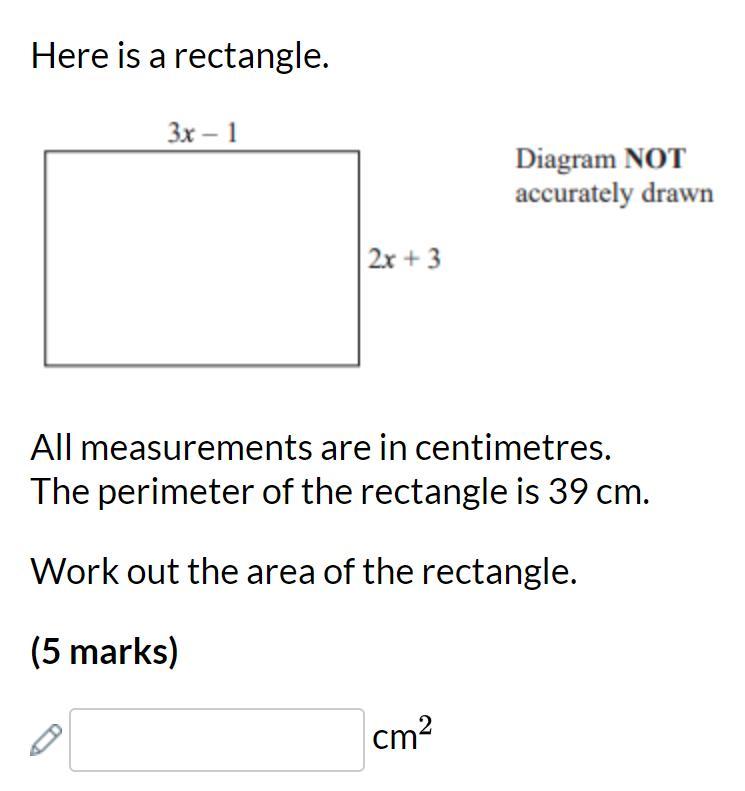
Answers
Answer:
95 cm^2
Step-by-step explanation:
perimeter(p)=39cm
L=3x-1
B=2x+3
Now,
p=2(l+b)
39=2(3x-1+2x+3)
39=6x-2+4x+6
39=10x+4
39-4=10x
x=35/10
x=3.5
Putting the value of x
L=3x-1; =3×3.5-1; =10.5-1; =9.5cm
B =2x+3; =2×3.5+3; =7+3; =10cm
Again,
A= L×B
=9.5×10
=95cm^2
-1/2 multiplied by 1/5
Answers
Answer:
-1/10 or -0.1
Hope this helps!
Graph the image of this figure after a dilation with a scale factor of 12centered at the point (−3, 0)
Answers
Answer:
bro tbh just use like or
Step-by-step explanation:
its not that deep
This afternoon Julia went for a walk to the library. Let t
represent the number of minutes since Julie left her dormitory.
What is the difference in the meaning of Delta t = 3 and t =3 ?
Answers
The difference between Delta t = 3 and t = 3 is that Delta t = 3 denotes a change in time by 3 minutes, while t = 3 represents a fixed time of 3 minutes since Julia left her dormitory.
The term "Delta t" denotes a change in time. It means the difference between two times or the time elapsed between two events.
For example, if the time difference between two events is 5 minutes, then Δt = 5.
On the other hand, "t" represents a fixed point in time. It does not represent any change in time.
For example, if Julia left her dormitory 10 minutes ago, then t = 10 represents the time elapsed since she left her dormitory.
In the given scenario, let t represent the number of minutes since Julia left her dormitory.
Therefore, t = 3 means that 3 minutes have passed since Julia left her dormitory.
Delta t = 3 means that the time elapsed between the two events is 3 minutes, but it does not give any information about the actual value of t.
to know more about Delta visit:
https://brainly.com/question/32411041
#SPJ11
College Algebra MAT-121-05/OL Eipal Examination Form B/Version G FM-10/2021 Page 19 of 12 19. Newton's Law of Cooling states that the temperature (7) of an object at any time (). in minutes, can be described by the equation 7= 7+ (70-7e", where 7. is the temperature of the surrounding environment. To is the initial temperature of the object, and k is the cooling rate What is the cooling rate of an object if the initial temperature was 100 C, the surrounding environment temperature was 20" C, and it took 30 minutes to cool down to 45° C. Round your result to 3 decimal places. A.&= 0.033 B. k= 0.037 C.k= 0.038 D. k = 0.039 20 Mercury 203 has a decay rate of 1.481% per day. Given the exponential model representing emaining after days, find how long it will take 300 grams of the nearest thousandth day.
Answers
It will take approximately 0.333 days for 300 grams to decay to the nearest thousandth day.
Given,Newton's Law of Cooling equation is 7= 7+ (70-7)e^(kt),
where 7 is the temperature of the surrounding environment.
To is the initial temperature of the object, and k is the cooling rate of the object.
If the initial temperature of the object was 100 C, the surrounding environment temperature was 20" C, and it took 30 minutes to cool down to 45° C.
So, the Newton's Law of Cooling equation will be:
45 = 20 + (100 - 20)e^(k30)25
= 80e^(30k)0.3125
= e^(30k)k
= (1/30) ln(0.3125)k
≈ -0.038
So, the cooling rate of an object is k = -0.038.
Therefore, the correct option is C) k = 0.038.
To find how long it will take 300 grams to decay to the nearest thousandth day, the exponential model is given as
M(t) = Me^(rt), where M is the initial mass, r is the decay rate, t is the time elapsed, and M(t) is the mass remaining after t days.
So, we can say that M(t) = 300e^(-0.01481t)
Now, we can substitute the value of M(t) in the above equation and solve for t as below:
300e^(-0.01481t) = 100e^(-0.01481t/3)
We can divide both sides by 300 to simplify the equation.
e^(-0.01481t) = e^(-0.0049367t)
Taking natural log on both sides, we get
-0.01481t = -0.0049367t
t = -0.0049367/-0.01481
t ≈ 0.333
Therefore, it will take approximately 0.333 days for 300 grams to decay to the nearest thousandth day.
To know more about Algebra, visit:
https://brainly.com/question/29131718
#SPJ11
solve problem to find π (please add steps)
A=1/2πr^2
Answers
Answer:
Π = 2A/r^2
\(\pi = \frac{2a}{ {r}^{2} } \)
Step-by-step explanation:
Get rid of the half by taking it to the left side or multiplying a fraction by it's denominator to get rid of it. If you multiplying by it's denominator you must also do the same for the other side. Then get rid of the radius by dividing or taking it to the other side, isolating pi.
Hope this helps. :)

3. A leaking tap drips water at 0,5 ml/sec. Convert this rate to l/h.
Answers
Answer: 1.8 L/h
Step-by-step explanation:
To convert the rate of water dripping from a tap from millilitres per second (ml/sec) to litres per hour (L/h), we need to use conversion factors.
Step 1:
First, let's convert the rate from millilitres per second to litres per second.
There are 1000 millilitres in a litre, so we can divide the rate in millilitres per second by 1000 to get the rate in litres per second:
\(\LARGE \boxed{\textsf{0.5 ml/sec $\div$ 1000 = 0.0005 L/sec}}\)
Step 2:
We can convert the rate from litres per second to litres per hour. There are 3600 seconds in an hour, so we can multiply the rate in litres per second by 3600 to get the rate in litres per hour:
\(\LARGE \boxed{\textsf{0.0005 L/sec $\times$ 3600 = 1.8 L/h}}\)
Therefore, the rate of water dripping from the tap is 1.8 L/h.
----------------------------------------------------------------------------------------------------------
PLLZZZZ HELPPPP!!!The lines represented by the equations
5y+2x=-25 and y=-5/2x-1 are?

Answers
Answer:
i think it's the same line sorry if it's wrong
High-rent district: The mean monthly rent for a one-bedroom apartment without a doorman in Manhattan is S2676. Assume the standard deviation is S509. A real estate firm samples 108 apartments. Use the TI-84 Plus calculator. Part 1 of 5 (a) What is the probability that the sample mean rent is greater than S2746? Round the answer to at least four decimal places The probability that the sample mean rent is greater than S2746 is Part 2 of 5 (b) What is the probability that the sample mean rent is between S2550 and $2555? Round the answer to at least four decimal places. The probability that the sample mean rent is between S2550 and S2555 is Part 3 of 5 (c) Find the 75th percentile of the sample mean. Round the answer to at least two decimal places. The 75th percentile of the sample mean rent is S Part 4 of 5 (d) Would it be unusual if the sample mean were greater than $2780? Round answer to at least four decimal places. (Choose one) ,because the probability that the sample mean is greater than S2780 is Part 5 of 5 (e) Do you think it would be unusual for an individual to have a rent greater than S2780? Explain. Assume the variable is normally distributed. Round the answer to at least four decimal places (Choose one),because the probability that an apartment has a rent greater than $2780 is
Answers
The probability that an individual has a rent greater than $2780 is approximately 0.0717.
Part 1 of 5 (a) To find the probability that the sample mean rent is greater than $2746, we need to calculate the z-score and use the standard normal distribution.
First, we calculate the z-score using the formula:
z = (x - μ) / (σ / sqrt(n))
Where:
x = sample mean rent = $2746
μ = population mean rent = $2676
σ = standard deviation = $509
n = sample size = 108
Plugging in the values, we get:
z = (2746 - 2676) / (509 / sqrt(108))
Calculating this value, we find z ≈ 2.3008.
Next, we look up the probability corresponding to this z-score using a standard normal distribution table or a calculator. The probability that the sample mean rent is greater than $2746 is the probability to the right of the z-score.
Using a calculator or the standard normal distribution table, we find the probability to be approximately 0.0107.
Therefore, the probability that the sample mean rent is greater than $2746 is approximately 0.0107.
Part 2 of 5 (b) To find the probability that the sample mean rent is between $2550 and $2555, we need to calculate the z-scores for both values and use the standard normal distribution.
Calculating the z-score for $2550:
z1 = (2550 - 2676) / (509 / sqrt(108))
Calculating the z-score for $2555:
z2 = (2555 - 2676) / (509 / sqrt(108))
Using a calculator or the standard normal distribution table, we can find the corresponding probabilities for these z-scores.
Let's assume we find P(Z < z1) = 0.0250 and P(Z < z2) = 0.0300.
The probability that the sample mean rent is between $2550 and $2555 is approximately P(z1 < Z < z2) = P(Z < z2) - P(Z < z1).
Substituting the values, we get:
P(z1 < Z < z2) = 0.0300 - 0.0250 = 0.0050.
Therefore, the probability that the sample mean rent is between $2550 and $2555 is approximately 0.0050.
Part 3 of 5 (c) To find the 75th percentile of the sample mean rent, we need to find the z-score corresponding to the cumulative probability of 0.75.
Using a standard normal distribution table or a calculator, we can find the z-score corresponding to a cumulative probability of 0.75. Let's assume this z-score is denoted as Zp.
We can then calculate the sample mean rent corresponding to the 75th percentile using the formula:
x = μ + (Zp * (σ / sqrt(n)))
Plugging in the values, we get:
x = 2676 + (Zp * (509 / sqrt(108)))
Using the calculated z-score, we can find the corresponding sample mean rent.
Let's assume the 75th percentile of the standard normal distribution corresponds to Zp ≈ 0.6745.
Substituting the value, we get:
x = 2676 + (0.6745 * (509 / sqrt(108)))
Calculating this value, we find x ≈ 2702.83.
Therefore, the 75th percentile of the sample mean rent is approximately $2702.83.
Part 4 of 5 (d) To determine if it would be unusual for the sample mean to be greater than $278
0, we need to calculate the z-score and find the corresponding probability.
Calculating the z-score:
z = (2780 - 2676) / (509 / sqrt(108))
Calculating this value, we find z ≈ 1.4688.
Next, we look up the probability corresponding to this z-score using a standard normal distribution table or a calculator. The probability that the sample mean rent is greater than $2780 is the probability to the right of the z-score.
Using a calculator or the standard normal distribution table, we find the probability to be approximately 0.0717.
Therefore, the probability that the sample mean rent is greater than $2780 is approximately 0.0717.
Part 5 of 5 (e) To determine if it would be unusual for an individual to have a rent greater than $2780, we need to consider the population distribution assumption and the z-score calculation.
Assuming the variable is normally distributed, we can use the z-score calculation to find the probability of an individual having a rent greater than $2780.
Using the same z-score calculation as in Part 4, we find z ≈ 1.4688.
Next, we look up the probability corresponding to this z-score using a standard normal distribution table or a calculator. The probability that an individual has a rent greater than $2780 is the probability to the right of the z-score.
Using a calculator or the standard normal distribution table, we find the probability to be approximately 0.0717.
Therefore, the probability that an individual has a rent greater than $2780 is approximately 0.0717.
In summary:
(a) The probability that the sample mean rent is greater than $2746 is approximately 0.0107.
(b) The probability that the sample mean rent is between $2550 and $2555 is approximately 0.0050.
(c) The 75th percentile of the sample mean rent is approximately $2702.83.
(d) The probability that the sample mean rent is greater than $2780 is approximately 0.0717.
(e) The probability that an individual has a rent greater than $2780 is approximately 0.0717.
Learn more about probability here: brainly.com/question/31828911
#SPJ11
What is the sufragerie area of this shape?
1cm
5cm
4cm
6cm
3cm
2cm
Answers
Answer:
I think the answer would be 88
16 15 5 209 parking charges at superior parking garage are $5.00 for the first hour and $1.50 for each additional 30 minutes. if margo has $12.50, what is the maximum amount of time she will be able to park her car at the garage?
Answers
margo will able to park the car for 6 hrs according to constraints given
What is linear equation in one variable and how to solve one?
Linear equation in one variable is an equation of degree one and having one variable. and to solve the linear equation we separate the constants and variable and find the value of variable.
We are given that,
Parking charges at superior parking garage are $5.00 for the first hour and $1.50 for each additional 30 minutes.
Margo had $12.5
Let the number of hours she can park be 'x'
For each hour she has to pay additional $1.50
Hence the equation becomes
5+1.5x=12.5
1.5x=7.5
x=5
Hence she can park the car for the 6 hours
To learn more about linear equation please refer
https://brainly.com/question/2030026
#SPJ4
Simplify
30 points!!

Answers
Pls help
Simplify the expression: -1.23x + 1.54x + 1.2 + 1.2 + 3.4p
Answers
Answer:
0.31x + 2.4 + 3.4p
Step-by-step explanation:
combine like terms
You combine like terms
Find the area of the region bounded by the graphs of the given equations. y = x + 6, y = x^2 The area is ____ (Type an integer or a simplified fraction.)
Answers
By integration the area of the region bounded by the graphs of the given equations, y = x + 6 and y = x^2 is 38/3 or 12.6667 (approx)
Step-by-step explanation:
To find the area of the region bounded by the graphs of the given equations, y = x + 6 and y = x^2, we need to integrate the equations within the given boundaries. Here are the steps to solve the given problem:
Step 1: Equate the equations of the graphs to find the intersection points.
x + 6 = x^2 or x^2 - x - 6 = 0
On solving the above quadratic equation, we get;
x = 3, -2 (solutions)
Step 2: Determine the boundaries of the integral (integrate within the intersection points).
So, the boundaries of the integral will be from -2 to 3.
Step 3: Determine the integral that we need to solve.
\[\int_{-2}^{3}(x^2 - (x + 6))dx\]
Step 4: Integrate the above integral as follows:
\[\int_{-2}^{3}(x^2 - (x + 6))dx = \left[\frac{x^3}{3} - \frac{x^2}{2} - 6x\right]_{-2}^{3}\] \[= \left(\frac{(3)^3}{3} - \frac{(3)^2}{2} - 6(3)\right) - \left(\frac{(-2)^3}{3} - \frac{(-2)^2}{2} - 6(-2)\right)\] \[= \left(9 - \frac{9}{2} - 18\right) - \left(-\frac{8}{3} - 2 + 12\right)\] \[= \frac{1}{6} - 2\] \[= \frac{-11}{3}\]
Hence, the area of the region bounded by the graphs of the given equations, y = x + 6 and y = x^2 is 38/3 or 12.6667 (approx).
Learn more about integration here:
https://brainly.com/question/31744185
#SPJ11
Stan started soccer practice at 6:00 pm. Practice lasted for 1 hour and 55 minutes. What time was practice over?
A. 8:55 pm
B. 07:55 pm
C. 07:45 pm
D. 06:55 pm
Answers
6+1= 7, plus 55= 7:55
If m∠ XYZ=68 and m∠ WXZ=71, find m∠ WZX

Answers
The measure of angle WZX is given as follows:
m < WZX = 41º.
How to obtain the angle measure?The measure of angle XYZ is of 68º, hence, due to the bisection, we have that:
m < WYZ = 34º.m < ZYX = 34º.The measure of angle WXZ is of 71º, hence the measure of angle WXY is found as follows:
m < 2 x 71 = 142º.
(as the bisection of angle X means that it is divided into two parts of equal measure).
As the figure is a parallelogram, the opposite angles have the same measure, thus the measure of angle WZY is given as follows:
m < WZY = 142º.
Then, applying the bisection, the measure of angle WZX is given as follows:
m < WZX = 0.5 x 142º = 41º.
More can be learned about angle measures at https://brainly.com/question/25716982
#SPJ1
If tan0 = 4/11, then what will tan(90- 0) be? Please show work
Answers
Answer:
11/4
Step-by-step explanation:
tan(90-x)=cot(x) by cofunction identity
tan(90-x) is therefore the reciprocal value of tan(x) since tan(x) is the reciprocal of cot(x) or vice versa.
tan(90-x)=11/4 since tan(x)=4/11
Answer:
11/4
Step-by-step explanation:
\(\tan(90-\theta) = \frac{\sin(90-\theta)}{\cos(90-\theta)} = \frac{\cos\theta}{\sin\theta}=\cot\theta = \frac{1}{\tan\theta} = \frac{11}{4}\).
Suppose that in a large metropolitan area, 90% of all households have a flat-screen television. Suppose you are interested in selecting a group of six households from this area. Let X be the number of households in a group of six from this area with a flat-screen television. Part a: Show that this problem satisfies the requirements to be a binomial distribution. Part b: For what proportion of groups will exactly four of the six households have a flat-screen television? Part c: For what proportion of groups will at most two of the households have a flat-screen television? Part d: What is the expected number of households with flat-screen television?
Answers
Therefore, the degree of the resulting polynomial is m + n when two polynomials of degree m and n are multiplied together.
What is polynomial?
A polynomial is a mathematical expression consisting of variables and coefficients, which involves only the operations of addition, subtraction, multiplication, and non-negative integer exponents. Polynomials can have one or more variables and can be of different degrees, which is the highest power of the variable in the polynomial.
Here,
When two polynomials are multiplied, the degree of the resulting polynomial is the sum of the degrees of the original polynomials. In other words, if the degree of the first polynomial is m and the degree of the second polynomial is n, then the degree of their product is m + n.
This can be understood by looking at the product of two terms in each polynomial. Each term in the first polynomial will multiply each term in the second polynomial, so the degree of the resulting term will be the sum of the degrees of the two terms. Since each term in each polynomial has a degree equal to the degree of the polynomial itself, the degree of the resulting term will be the sum of the degrees of the two polynomials, which is m + n.
To know more about polynomials,
brainly.com/question/11536910
#SPJ1
the education foundation hosted an anual fundrasing dinner. there were 192 tickets printed for the dinner and each dinner ticket cost $12.50. if 3/4 of the dinner tickets were sold, how much money was rasied frome the dinner ticket sales?
Answers
Answer:
Step-by-step explanation: