2)
A line passes through the points (0.5) and (-6,3). A second line passes through
(-15, 0) and (-21, -2).
A) Do the lines intersect? Show work to prove it! Grcle YES or
NO
Answers
Answer:
Step-by-step explanation:
Find the slope of each line. If the slopes are the same, the lines are parallel. Otherwise, the lines intersect.
Slope of line passing through (x₁, y₁) and (x₂, y₂) = (y₂-y₁)/(x₂-x₁)
Slope of line passing through (0, 5) and (-6, 3) = (3-5)/(-6-0) = ⅓
Slope of line passing through (-15, 0) and (-21, -2) = (-2-9)/(-21-(-2)) = 11/19
The lines intersect.
Related Questions
what is the size of the angle between north west and south east?
Answers
180°
Step-by-step explanation:Size of the angle between:North and South: 180°East and West: 180°North East and South West: 180°North West and South East: 180°North West and North East: 90°South West and South East: 90°(dy/dx) = e^(3x+2y)
solve the differential equation by separation of variables
Answers

how would you interpret an individual player’s 3P%?
Answers
Answer:
A high 3P% indicates that the player is an accurate shooter from the three-point line, making them a scoring threat and potentially creating spacing on the floor for their team.
Step-by-step explanation:
1)Find f(23)?(4) for the Taylor series for f(x) centered at 4 iff(x) = \sum_{n=0}^{Infinity}(n+3)(x-4^n)/(n+1)!2)Find the Taylor series for f(x) centered at the given value of a. [Assume that f has a power series expansion. Do not show that Rn(x) ? 0.]f(x)=\frac{8}{x} a = -2
Answers
1. The Taylor series for f(x) centered at 4 if \(f(x) = \sum_{n=0}^{Infinity}(n+3)(x-4^n)/(n+1)!2)\) is \(f(23.4) = \sum_{n=0}^{Infinity}(n+3)(23.4-4^n)/(n+1)!\)
2. The Taylor series for f(x) centered at the given value of a is f(x) = -4 + 2(x+2) - (2/3)(x+2)² + (4/3)(x+2)³ - ...
1. To find the Taylor series for f(x) centered at 4, we need to first find the derivatives of f(x):
\(f(x) = \sum_{n=0}^{Infinity}(n+3)(x-4^n)/(n+1)!f'(x) = \sum_{n=1}^{Infinity}(n+2)(x-4^{n-1})/n!\\f''(x) = \sum_{n=2}^{Infinity}(n+1)(x-4^{n-2})/(n-1)!\\f'''(x) = \sum_{n=3}^{Infinity}(n)(x-4^{n-3})/(n-2)!\\\)
and so on. Note that for all derivatives of f(x), the constant term is zero.
Now, to find f(23.4), we can substitute x = 23.4 into the Taylor series for f(x) centered at 4 and simplify:
\(f(x) = \sum_{n=0}^{Infinity}(n+3)(x-4^n)/(n+1)!\\f(23.4) = \sum_{n=0}^{Infinity}(n+3)(23.4-4^n)/(n+1)!\)
The series converges by the Ratio Test, so we can evaluate it numerically to find f(23.4).
2. To find the Taylor series for f(x) centered at a = -2, we can use the formula:
\(f(x) = \sum_{n=0}^{Infinity}f^{(n)}(a)/(n!)(x-a)^n\)
where f^{(n)}(a) denotes the nth derivative of f(x) evaluated at a.
First, we find the derivatives of f(x):
f(x) = 8/x
f'(x) = -8/x²
f''(x) = 16/x³
f'''(x) = -48/x⁴
and so on. Note that all derivatives of f(x) have a factor of 8/x^n.
Next, we evaluate each derivative at a = -2:
f(-2) = -4
f'(-2) = 2
f''(-2) = -2/3
f'''(-2) = 4/3
and so on.
Finally, we substitute these values into the formula for the Taylor series to obtain:
f(x) = -4 + 2(x+2) - (2/3)(x+2)² + (4/3)(x+2)³ - ...
Note that the radius of convergence of this series is the distance from -2 to the nearest singularity of f(x), which is x = 0. Therefore, the radius of convergence is R = 2.
To know more about Taylor series here
brainly.com/question/29733106
#SPJ11
Find the other endpoint of the line segment with the given endpoint -5, 2 and midpoint 2, -5
Answers
Answer:
( 9, -12 )
Step-by-step explanation:
Mario's Math Tutoring
you have the midpoint
2, -5
use the midpoint formula
(x1+x2)/2 , (y1+y2)/2
to get the endpoint
x :
(-5+x2)/2 = 2
(-5+x2) = 4
-5+x2 = 4
x2 = 9
y:
(2+y2)/2 = -5
(2+y2) = -10
2+y2 = -10
y2 = -12
Thank you Mario!
Help help helpppp helppp

Answers
B. -11
Hope it helps
Write (x^2)^4 without any exponents.
Answers
Answer:
(x * x) * (x * x) * (x * x) * (x * x)
Step-by-step explanation:
(y^4) is the same thing as y * y * y * y
so for y = (x^2), we can write (x^2)^4 as:
(x^2) * (x^2) * (x^2) * (x^2)
and each (x^2) is just x * x
so, this is how you can write it!
(x * x) * (x * x) * (x * x) * (x * x)
Answer:
x+x+x+x+x+x+x+x or xxxx*xx or x*x x*x x*x x*x
Step-by-step explanation:
Nabhita measure the volume of a sink basin by modeling it as a hemisphere. Nabhita measures its radius to be 15 1/4 inches. Find the sinks volume in cubic inches. Round your answer to the nearest tenth if possible
Answers
Answer:
7427.9 cubic inches. Depending on how accurate your answer is supposed to be, this answer might be wrong (for example, if they ask you to use 3.14 for pi.)
Step-by-step explanation:
The formula for the volume of a hemisphere is (2/3)πr³.
(2/3)π(15.25)³
=(2/3)π(61/4)³
.=7427.93585525
Rounded to the nearest tenth, this is 7427.9 cubic inches.
Three numbers A, B and C are in the ratio 7: 2: 4. The sum of the three numbers is 104. What is the number C?
Answers
Answer:
C = 32
Step-by-step explanation:
The numbers are in the ratio 7 : 2 : 4 = 7x : 2x : 4x ( x is a multiplier ) , then
7x + 2x + 4x = 104
13x = 104 ( divide both sides by 13 )
x = 8
Thus C = 4x = 4 × 8 = 32
3^5*2^-6 please answer fast
Answers
\(3^5 \cdot 2^{-6}=\dfrac{3^5}{2^6}=\dfrac{243}{64}\)
7) Find the midpoint of the line segment joining the points P₁ and P₂.
P1 = (1,3); P2 = (6,8)
Answers
\(~~~~~~~~~~~~\textit{middle point of 2 points } \\\\ P1(\stackrel{x_1}{1}~,~\stackrel{y_1}{3})\qquad P2(\stackrel{x_2}{6}~,~\stackrel{y_2}{8}) \qquad \left(\cfrac{ x_2 + x_1}{2}~~~ ,~~~ \cfrac{ y_2 + y_1}{2} \right) \\\\\\ \left(\cfrac{ 6 +1}{2}~~~ ,~~~ \cfrac{ 8 +3}{2} \right) \implies \left(\cfrac{ 7 }{2}~~~ ,~~~ \cfrac{ 11 }{2} \right)\implies \left(3\frac{1}{2}~~,~~5\frac{1}{2} \right)\)
Need help don’t like math help

Answers
Answer:
$21.81
Step-by-step explanation:
add the reduced number to the new number
Answer:
21.81
Step-by-step explanation:
add 1.05 to 20.76
In a class of 27 students, 18 are female and 8 have an A in the class. There are 2
students who are female and have an A in the class. What is the probability that a
student chosen randomly from the class has an A?
Answers
Answer:
8/27
Step-by-step explanation:
Given:
In a class of 27 students, 18 are female and 8 have an A in the class. There are 2 students who are female and have an A in the class.
To Find:
What is the probability that a student chosen randomly from the class has an A?
Solve:
Given:
Total : 27
Female : 18
A : 8
A Female : 2
Therefore,
8/27
Kavinsky
the wheels on the bus go….?
Answers
Answer:
Round and round x2
Step-by-step explanation:
like a song hope this helps.
Which two expressions are equivalent

Answers
Answer: The choice with the two equivalent expressions is B.
Step-by-step explanation:
Here's how I got my answer:
Do each equation carefully and be sure to pay attention to the order of the multiplication, subtraction, addition, parentheses and division signs. Since B. is just the Associative Property (it means that it has been grouped in a different way) then it is the same as the first equation.
The sum of the digits of a two-digit number is seventeen. The number with the digits reversed is thirty more than 5 times the tens' digit of the original number. What is the original number?
Answers
Therefore, the original number is 10x + y = 10(10) + 7 = 107.
Given that the sum of the digits is seventeen, we have the equation:
x + y = 17 (equation 1)
The number with the digits reversed is thirty more than 5 times the tens' digit of the original number. The number with the digits reversed would be 10y + x.
According to the given information, we have the equation:
10y + x = 5x + 30 (equation 2)
To solve the system of equations, we can substitute equation 1 into equation 2:
10(17 - x) + x = 5x + 30
Expanding and simplifying:
170 - 10x + x = 5x + 30
170 - 30 = 5x + 10x - x
140 = 14x
x = 10
Substituting the value of x back into equation 1:
10 + y = 17
y = 7
Therefore, the original number is 10x + y = 10(10) + 7 = 107.
Learn more about original number here
https://brainly.com/question/1343101
#SPJ11
Jonah needs to determine the dimensions of a rectangular poster that will cover an area represented by
7x² + 3x - 10. Which of the following expressions is equivalent to the area of the rectangular poster?
A (x+1)(7x-10)
B (x-1)(-7x+10)
C(x-1)(7x+10)
D(x-7)(x+10)
E(7x-1)(x+10)
Answers
Answer:
The correct answer is A (x+1)(7x-10).
Step-by-step explanation:
To determine the dimensions of a rectangular poster that will cover an area represented by 7x² + 3x - 10, we need to find the factors of the expression 7x² + 3x - 10 that will give us the length and width of the poster.
One way to do this is to factor the expression 7x² + 3x - 10 using the difference of squares method. We can write the expression as follows:
7x² + 3x - 10 = (7x² + 3x) - 10
To factor (7x² + 3x) - 10, we can write the expression as the difference of squares:
(7x² + 3x) - 10 = (7x² + 3x + 10) - (10 + 10)
To simplify the expression, we can complete the square for the terms in parentheses:
(7x² + 3x + 10) - (10 + 10) = (7x² + 3x + 10) - 20
To complete the square, we need to add and subtract the square of half the coefficient of the x term, which is (3/2)² = 9/4. We can rewrite the expression as follows:
(7x² + 3x + 10) - 20 = (7x² + 3x + 10 + 9/4) - (20 - 9/4)
To simplify the expression, we can factor the terms in parentheses:
(7x² + 3x + 10 + 9/4) - (20 - 9/4) = [(7x² + 3x + 10 + 9/4) - (20 - 9/4)]
To simplify the expression further, we can factor out a common factor:
[(7x² + 3x + 10 + 9/4) - (20 - 9/4)] = (x + 1)(7x - 10)
From the given options, the expression that represents the area of the rectangular poster is (x+1)(7x-10), which is equivalent to 7x² + 3x - 10. We can verify this by multiplying (x+1)(7x-10) to get 7x² + 3x - 10. Therefore, the correct answer is A (x+1)(7x-10).
Find the area of the figure. It is formed by two congruent trapezoids

Answers
The total area formed by the two congruent trapezoids in this problem is given as follows:
48 m².
How to obtain the area of a trapezoid?The area of a trapezoid is obtained adding the bases, multiplying by the height, and dividing by 2.
For the two congruent trapezoids in this problem, the parameters are given as follows:
Bases 3 and 9.Height of 8/2 = 4.Considering that there are two trapezoids, teh total area is given as follows:
A = 2 x 1/2 x (3 + 9) x 4
A = 12 x 4
A = 48 m².
More can be learned about the area of a trapezoid at https://brainly.com/question/1463152
#SPJ1
Joaquin is four more than half Marjorie’s age. Marjorie is also 32 less than three times Joaquin’s age.
How old is Marjorie?
Answers
Answer:
She is 40 years of age
Step-by-step explanation:
Let Joaquin age be j
Let Marjorie age be m
From the first part of the question;
j = 4 + m/2
Secondly;
m =3j - 32
Multiply equation i through by 2
2j = 8 + m
m = 2j-8
Equate both m
2j-8 = 3j-32
3j-2j = 32 -8
j = 24
m = 2j-8
m = 2(24)-8
m = 48-8
m = 40
someone pls help :(
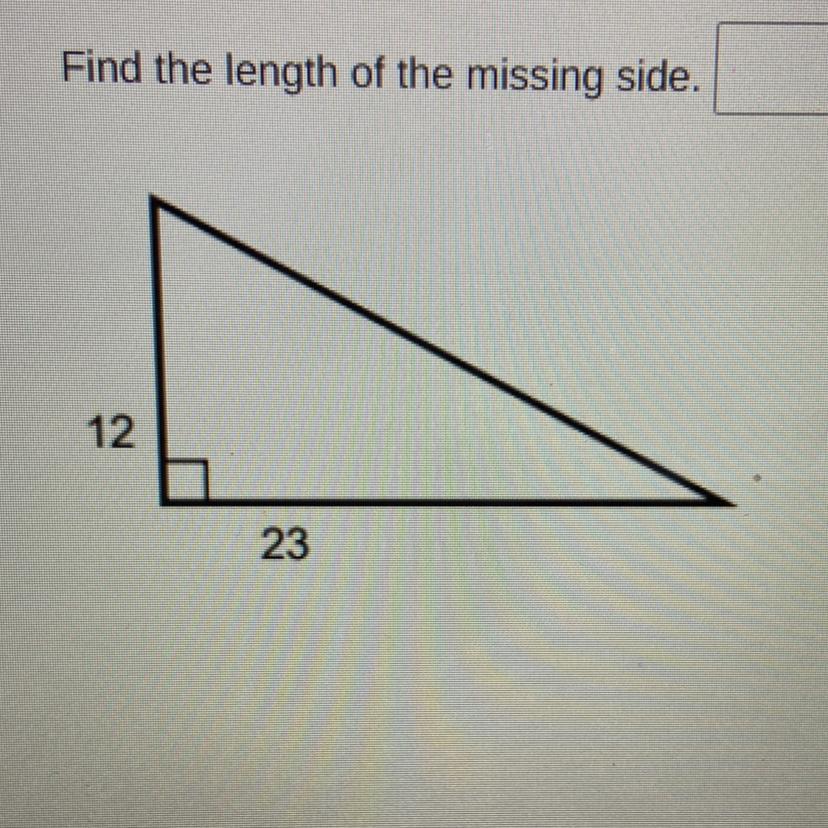
Answers
c= 25.9

tudent Name Finding Perimeter Directions: Find the perimeter of each rectangle. Be sure to include the correct unit. 10 ft 11 ft 11 ft 10 ft 2 9 m 4. 12 m 12 m 9 Cm 9m -4th Grade math
Answers
The perimeter : (a) 42 ft
(b) 42 ft
(c) 14.04 m
(d) 48 m
(e) 1818 cm
What is Perimeter?
In geometry, the perimeter is the total length of the boundary or the outer edge of a two-dimensional shape, such as a polygon. It is the addition of the lengths of all sides of the shape. The perimeter is measured in units of length, such as meters or feet.
(a) Rectangle with sides of 10 ft and 11 ft:
Perimeter = 2(10 ft) + 2(11 ft) = 20 ft + 22 ft = 42 ft
(b) Rectangle with sides of 11 ft and 10 ft:
Perimeter = 2(11 ft) + 2(10 ft) = 22 ft + 20 ft = 42 ft
(c) Rectangle with sides of 2.9 m and 4.12 m:
Perimeter = 2(2.9 m) + 2(4.12 m) = 5.8 m + 8.24 m = 14.04 m
(d) Square with sides of 12 m:
Perimeter = 4(12 m) = 48 m
(e) Rectangle with sides of 9 cm and 9 m:
Since the sides are in different units, we need to convert one of them to the other unit. Let's convert 9 m to cm:
9 m = 900 cm
Perimeter = 2(9 cm) + 2(900 cm) = 18 cm + 1800 cm = 1818 cm
To learn more about Perimeter visit the link:
https://brainly.com/question/19819849
#SPJ9
perform the translation (x, y) - (x-2, y+3)
Answers
Answer:
The coordinate of the image of a point is (2, +3) under the translation (x , y) → (x - 2),( y + 3). Find the coordinate of the preimage.
We are just looking for x and y and we know (2, +3) → (x - 2, y + 3)
2 = x - 2
x = 4
-3 = y + 3
y = -6
(x , y) = (4, -6)
How to find a
? can guys help me please?

Answers
Answer:
The range of this set of numbers is 9
Step-by-step explanation:
The range is the greatest number subtracted by the lowest number
in this problem that is 21-12
Answer:
9
Step-by-step explanation:
range = highest number in a set minus the lowest number in a set, in your case:
21 - 12 = 9
Please look at picture answer and explain work

Answers
Answer: The answer is D. 240 grams
Step-by-step explanation:
1. Find the volume.
2cm×3cm×5cm=30 cubic centimeters
2. Find the volume of the other box.
4cm×9cm×5cm=180 cubic centimeters.
3. Divide. 180÷30=6
4. 6 times the amount it can hold, 40=240 grams of clay.
Hope that helped!
Answer:
Step-by-step explanation:
we are told that the box is 2 cm high, 3 cm wide 5 cm long and holds 40 grams of clay
so 2*3*5 = 30 \(cm^{3}\)
so the 30 cubic centimeter volume holds 40 grams ( it would have been nice if they had let the box hold 30 grams but, no :(
40/30 = 1.333333 or 1 and \(\frac{1}{3}\) of a gram okay, sooooo now we know each cubic centimeter holds that much clay, now let's solve for how many cubic centimeters are in the bigger box, you can try to solve it 1st if you'd like to practice, below I solve it
twice the height so 2(2)=4 high
3 times the width , so 3(3) = 9 wide
same length, so 5 long
4*9*5 = 180
180*1.33333333333 = 240 grams of clay in 2nd bigger box :)
I'm sure there is a funny box joke in there some where :DDDD
do you get the math? :)
For the function below find a) the critical numbers; b) the open intervals where the function is increasing, and c) the open intervals where it is decreasing f(x)=8x³-42x-48x + 4 a) Find the critical number(s). Select the correct choice below and, if necessary fill in the answer box to complete your choice. A. The critical number(s) is/are (Type an integer or a simplified fraction. Use a comma to separate answers as needed
Answers
A) Function is increasing on (-∞, -1) and (7/2, ∞), and decreasing on (-1, 7/2).
b) The local minimum value of f is; 5608/2197 at x = -42/13, and the local maximum value of f is 139/8 at x = 7/2.
(a) To determine the intervals on which f is increasing or decreasing, we need to determine the critical points and then check the sign of the derivative on the intervals between them.
f(x)=8x³-42x-48x + 4
f'(x) = 24x² - 90
Setting f'(x) = 0, we get
24x² - 90 = 0
24x² = 90
x =± √3.75
So, the critical points are;
x = -1 and x = 7/2.
We can test the sign of f'(x) on the intervals as; (-∞, -1), (-1, 7/2), and (7/2, ∞).
f'(-2) = 72 > 0, so f is increasing on (-∞, -1).
f'(-1/2) = -25 < 0, so f is decreasing on (-1, 7/2).
f'(4) = 72 > 0, so f is increasing on (7/2, ∞).
Therefore, f is increasing on (-∞, -1) and (7/2, ∞), and decreasing on (-1, 7/2).
(b) To determine the local maximum and minimum values of f, we need to look at the critical points and the endpoints of the interval (-1, 7/2).
f(-1) = -49
f(7/2) = 139/8
f(-42/13) = 5608/2197
Learn more about maximum value here:
brainly.com/question/23504923
#SPJ4
1. The area of a rectangular carpet is X² + X - 2. HINT: Area = length X breadth
a). if X is a whole number, use factorization to find the length and the breadth of the carpet in terms of X.
b). if X = 2 m, find the actual dimensions of the carpet.
c). it costs R50 per square metre to make such this carpet. how much will it cost to manufacture 5 carpets?
Answers
Answer:
look above
Step-by-step explanation:
hopeit hepls

6. A particle is moving on a straight line such that a(t) = cost, s(0) = 0, v(0) = 5.
Find the position s(t) of the particle.
Answers
Step-by-step explanation:
St3-623t+4St3-623t+4V=St3-623t+4V=dsSt3-623t+4V=dsdtSt3-623t+4V=dsdtSo 3t²12 + 3 = vSt3-623t+4V=dsdtSo 3t²12 + 3 = vagain differentiate,a =St3-623t+4V=dsdtSo 3t²12 + 3 = vagain differentiate,a =6t - 12 = 0St3-623t+4V=dsdtSo 3t²12 + 3 = vagain differentiate,a =6t - 12 = 0t=2sSt3-623t+4V=dsdtSo 3t²12 + 3 = vagain differentiate,a =6t - 12 = 0t=2sv=3(2)² - 12 x 2+3=-9ms-1Seven less than 4 times the square of a number is 18. Find the two numbers.
Answers
The two numbers of seven less than 4 times the square of a number is 18 are -5/2 and 5/2
Let the unknown number be "x"
The square of an unknown number is expressed as x²4 times the square of a number is 4x²Seven less than 4 times the square of a number is 4x² - 7If the resulting expression is 18, this will be expressed as 4x² - 7 = 18
Solving the resulting expression
\(4x^2-7=18\\4x^2= 18+7\\4x^2=25\\x^2=\frac{25}{4}\\x=\pm \frac{5}{2}\)
Hence the two numbers of seven less than 4 times the square of a number is 18 are -5/2 and 5/2
Learn more here: https://brainly.com/question/13805464
Nima bought 10.5 yards of string for 3 art projects.
Each project will use 3.6 yards of string.
Answers
Based on the number of projects to be done and their length requirements, we can infer that the yards Nima bought were not enough.
There are 3 projects and each will require 3.6 yards. In total, they will require:
= 3 x 3.6
= 10.8 yards
Nima bought only 10.5 yards which means that Nima will be short by:
= 10.8 - 10.5
= 0.3 yards
In conclusion, Nima does not have enough string for all the projects.
Find out more about such calculations at https://brainly.com/question/793983.
-2/3 + [3/5 + -5/7]
HELP
Answers
Answer:
\(=-\frac{82}{105}\)
Step-by-step explanation:
\(-\frac{2}{3}+\left[\frac{3}{5}+\left(-\frac{5}{7}\right)\right]\)
\(\frac{3}{5}+\left(-\frac{5}{7}\right)\)
\(=-\frac{4}{35}\)
\(=-\frac{2}{3}-\frac{4}{35}\)
\(=-\frac{82}{105}\)
\(\huge\text{Hey there\bf!}\)
\(\mathsf{-\dfrac{2}{3} + [\dfrac{3}{5} + -\dfrac{5}{7}]}\)
\(\mathtt{= - \dfrac{2}{3} + \dfrac{3}{5} + - \dfrac{5}{7}}\)
\(\mathtt{= - \dfrac{2}{3} + \dfrac{3}{5} - \dfrac{5}{7}}\)
\(\mathtt{-\dfrac{2\times35}{3\times35} + \dfrac{3\times21}{5\times21} - \dfrac{5\times15}{7\times15}}\)
\(\mathtt{= -\dfrac{70}{105} + \dfrac{63}{105}- \dfrac{75}{105}}\)
\(\mathtt{= \dfrac{-70 + 63 - 75}{105 + 0 - 0}}\)
\(\mathtt{= \dfrac{-7 - 75}{105 - 0}}\)
\(\mathtt{= \dfrac{-82}{105}}\)
\(\mathtt{= -\dfrac{82}{105}}\)
\(\huge\text{Therefore your answer should be:}\)
\(\huge\boxed{\mathtt{\mathtt{= -\dfrac{82}{105}}}}\huge\checkmark\)
\(\huge\text{Good luck on your assignment \& enjoy your day!}\)
~\(\frak{Amphitrite1040:)}\)