1,872 words in 26 minutes. Find the unit rate.
Answers
Answer:
72 words per minute
Step-by-step explanation:
The unit rate in this case is words per minute. Therefore, the answer is 1872 / 26 = 72 words per minute.
Related Questions
Shawn’s weekly salary is $978.25. His employer is changing the pay period to semimonthly. What is Shawn’s annual salary? What will his semimonthly salary be?
Answers
Answer:
Annual Salary: $50,869
Semimonthly Salary: $1,956.50
Step-by-step explanation:
Semimonthly: Occurs twice a month
52 weeks in a year times weekly salary
978.25 x 52= 50,869
978.25 x 2= 1,956.50
Which static characteristics are desirable?
Answers
When it comes to static characteristics, there are many desirable attributes that can make a product or service stand out from the competition.
Quality and reliability are essential and desirable, as these are the main factors customers will consider when making a purchasing decision.
Durability is also important, as it ensures that a product will continue to perform to its highest standards over time.
Additionally, value for money is key, as customers want to be sure that they are getting a product or service that is worth the cost.
Furthermore, flexibility is highly desirable, as customers often need the ability to customize products or services according to their specific needs.
Finally, a good customer service experience is an essential static characteristic, as a positive customer experience can increase customer satisfaction and loyalty.
To learn more about static, click here:
https://brainly.com/question/26609519
#SPJ4
Example 4 A closed box has a fixed surface area A and a square base with side x. (a) Find a formula for the volume, V. of the box as a function of x. What is the domain of V? (b) Graph V as a function of x. (c) Find the maximum value of V.
use the work in example 4 in this section of the textbook to find a formula for the volume of a box having surface area 10.
Answers
The volume of the box with surface area 10 is given by the formula V = 2.5x^2 - 0.25x^4, where x is the length of a side of the square base.
To find a formula for the volume of the box with surface area A and square base with side x, we first need to find the height of the box. Since the box has a square base, the area of the base is x^2. The remaining surface area is the sum of the areas of the four sides, each of which is a rectangle with base x and height h. Therefore, the surface area A is given by:
A = x^2 + 4xh
Solving for h, we get:
h = (A - x^2) / 4x
The volume V of the box is given by:
V = x^2 * h
Substituting the expression for h, we get:
V = x^2 * (A - x^2) / 4x
Simplifying, we get:
V = (Ax^2 - x^4) / 4
The domain of V is all non-negative real numbers, since both x^2 and A are non-negative.
To graph V as a function of x, we can use a graphing calculator or plot points using a table of values. The graph will be a parabola opening downwards, with x-intercepts at 0 and sqrt(A) and a maximum at x = sqrt(A) / sqrt(2).
To find the maximum value of V, we can take the derivative of V with respect to x and set it equal to 0:
dV/dx = (2Ax - 4x^3) / 4
Setting this equal to 0 and solving for x, we get:
x = sqrt(A) / sqrt(2)
Plugging this value of x into the formula for V, we get:
V = A^1.5 / (4sqrt(2))
Therefore, the maximum value of V is A^1.5 / (4sqrt(2)).
To find the formula for the volume of a box having surface area 10, we simply replace A with 10 in the formula we derived earlier:
V = (10x^2 - x^4) / 4
Simplifying, we get:
V = 2.5x^2 - 0.25x^4
Therefore, the volume of the box with surface area 10 is given by the formula V = 2.5x^2 - 0.25x^4, where x is the length of a side of the square base. The domain of V is all non-negative real numbers.
Learn more about : General Geometry - https://brainly.com/question/31426425
#SPJ11
Anybody know how to do the following?.. Which Similarity statement can you write relating the three triangles in the diagram below?

Answers
Answer:
I believe the answer is D
Step-by-step explanation:
if you want an explanation let me know and have a great day and I'm 100% sure that D is the right answer
Expand.
a)3(x - 2)
b)2(y + 4)
c)8(3 + x)
Answers
Answer:
\(a \: 3x - 6 \\ b \: 2y + 8 \\ c \: 8x + 24\)
Step-by-step explanation:
All we have to do is multiply accordingly. I'll use a for an example.
So for the value before the perentheses we multiply that by all of the values in the perentheses.
\(3x \: and \: - 6\)
So the correct answer would be
\(3x - 6\)
You can use the same strategy for all the questions, but I'll just answer those straight away.
Also you may notice I put the variable before the constant in question c because the variable should always go before the constant in expressions and equations.
you rent an apartment that cost 1600 per month during the first year but the rest had to go by 12.5 per year what would be the rent of the apartment during the 10th year in
Answers
Answer: 2000
12.5÷100=0.125
1600×0.125×10=2000
A right triangle has legs of 30 inches and 40 inches whose sides are changing. The short leg is increasing by 5 in/sec and the long leg is shrinking at 7 in/sec. What is the rate of change of the hypotenuse?
Answers
That is a change in the hypotenuse's length of -2.6 inches per second.
What in math is a rate?
A rate is a unique ratio where the two words are expressed in several units. For instance, the price is 69 for 12 ounces if a 12-ounce can of maize costs 69. This is not a proportion of two comparable units, like shirts. This ratio compares two dissimilar units: ounces and cents
h = sqr(b^2 + a^2), b=30, a=40, b'=-5, a'=-7
h' = [(1/2)/sqr(b^2+a^2)](2bb' + 2aa') = sqr(30^2+40^2)(30(5)+40(-7)
= (150-280)/sqr2500 = (-130)/50 =-- -13/5 = -2.6 inches per second
2.6 inches are lost from the hypotenuse every second.
Check the response by observing what transpires in one second.
30 to 35 on the short leg
greater leg descends from 40 to 37
From 50 to 47.4 is the hypotenuse
In one second, 50-47.4 equals a 2.6 reduction. That is a change in the hypotenuse's length of -2.6 inches per second.
Learn more about rate
brainly.com/question/119866
#SPJ1
Find the missing lengths of the sides.

Answers
Find the solution to the linear system of differential equations {x′= 22x + 60y, y′= -6x - 16y
satisfying the initial conditions satisfying the initial conditions x(0)=5 and y(0)=3:
Answers
The solution to the system of differential equations that satisfies the initial conditions x(0)=5 and y(0)=3 is:
x(t) = (29/3) \(e^{\frac{22t}{3} }\) - (4/3) \(e^{\frac{-16t}{3} }\)
y(t) = (-13/3) \(e^{\frac{22t}{3} }\) + (2/3) \(e^{\frac{-16t}{3} }\)
To solve the system of differential equations, we can use matrix exponential. The system can be written in matrix form as follows:
X' = AX, where X = [x y], A = [22 60; -6 -16]
The matrix exponential of A can be calculated as follows:
\(e^{(At)}\) = I + At + \(\frac{(At)^{2}}{2!}\) + \(\frac{(At)^{3}}{3!}\) + ...
where I is the identity matrix and t is the variable of integration.
We can substitute A and t = 1 into the formula to get:
\(e^{A}\)= I + A + \(\frac{(A)^{2}}{2!}\) + \(\frac{(A)^{3}}{3!}\)+ ...
= [1 0; 0 1] + [22 60; -6 -16] + [44 192; -36 -104]/2! + [ -256 -768; 96 272]/3! + ...
= [1 + 22 + \(\frac{44}{2!}\) - \(\frac{256}{3!}\)*60 + \(\frac{192}{2!}\) - \(\frac{768}{3!}\);
-6 + \(\frac{(-6)}{2!}\) + \(\frac{96}{3!}\) - 16 + \(\frac{(-104)}{2!}\)+ \(\frac{272}{3!}\)]
= [\(\frac{29}{3}\) \(\frac{102}{3}\);
\(\frac{-13}{3}\) \(\frac{-4}{3}\) ]
Now we can use the initial conditions to find the constants of integration. We have:
X(0) = [x(0) y(0)] = [5 3]
So,
[\(e^{A}\)] [\(c_{1}\)] = [5]
[\(c_{2}\)] [3]
Multiplying both sides by the inverse of \(e^{A}\), we get:
[\(c_{1}\)] = [29/3 102/3]^(-1) [5]
[\(c_{2}\)] [-13/3 -4/3] [3]
Solving this system of linear equations, we get:
\(c_{1}\) = -4/3
\(c_{2}\) = 2/3
Therefore, the solution to the system of differential equations that satisfies the initial conditions x(0)=5 and y(0)=3 is:
x(t) = (29/3) \(e^{\frac{22t}{3} }\) - (4/3) \(e^{\frac{-16t}{3} }\)
y(t) = (-13/3) \(e^{\frac{22t}{3} }\) + (2/3) \(e^{\frac{-16t}{3} }\)
To learn more about differential equations:
https://brainly.com/question/14620493
#SPJ4
in the hertzsprung–russell diagram, how does the position of a typical star change while it is at the main-sequence phase of its evolution?
Answers
The position of a typical star on the HR diagram changes during its main-sequence phase, with more massive stars shifting toward the upper left due to increasing luminosity and lower-mass stars moving toward the lower right due to decreasing temperature.
In the Hertzsprung-Russell (HR) diagram, the main sequence represents the phase of a star's evolution when it is actively fusing hydrogen in its core. During this phase, the position of a typical star on the main sequence can change, and option D provides an accurate explanation.
Massive stars, with a mass of around 4 solar masses or more, have a higher luminosity compared to lower-mass stars. As these massive stars evolve, their luminosity increases, causing them to move toward the upper left region of the HR diagram. This shift is because higher luminosity corresponds to a larger radius and a higher surface temperature for massive stars.
On the other hand, lower-mass stars, like our Sun, have lower luminosity. As they evolve, their luminosity decreases, leading them to move toward the lower right region of the HR diagram. This movement occurs as the star exhausts its hydrogen fuel, causing its core to contract and its surface temperature to decrease.
Therefore, the position of a typical star on the HR diagram changes during its main-sequence phase, with more massive stars shifting toward the upper left due to increasing luminosity and lower-mass stars moving toward the lower right due to decreasing temperature.
To know more about luminosity check the below link:
https://brainly.com/question/28332746
#SPJ4
Incomplete question:
In the Hertzsprung-Russell diagram, how does the position of a typical star change while it is at the main-sequence phase of its evolution?
A) A star's position on the main sequence is determined only by its mass, not its age, so stars do not move along the main sequence during evolution.
B) Stars move from upper right to lower left while they are on the main sequence.
C) Stars move from upper left to lower right while they are on the main sequence.
D) Massive stars (4 solar masses) move toward the upper left as their luminosity increases, while lower-mass stars move toward the lower right as their temperature decreases.
Parveen scored 18 out of 25 in a maths test. What percentage did she score
Answers
Answer:
72%
Step-by-step explanation:
Express her score as a fraction and multiply by 100% to make the percentage
\(\frac{18}{25}\) × 100% = 18 × 4% = 72%
Answer:
72%
Step-by-step explanation:
Total score of Parveen in her math test
= 18/25
Total percentage she scored in her math test
= (18/25×100)%
= (18×4)%
= 72%
Hence, Parveen scored 72% in her math test.
Practising
5. Write an equation for the diagram. Solve
your equation. Show your steps.
n
n
n
n
n

Answers
Solve?
6n+4=28
-4
6n=24
Divide by 6
N=4
Evaluate 6 + 4 a + b 3 6+ a 4 + 3 b 6, plus, start fraction, 4, divided by, a, end fraction, plus, start fraction, b, divided by, 3, end fraction when a = 4 a=4a, equals, 4 and b = 3 b=3
Answers
Answer:
The answer is 8
Step-by-step explanation:
Evaluate
6 + 4/a + b/3
When a = 4, b = 3
Substitute the values of a and b into the expression
6 + 4/4 + 3/3
= 6 + 1 + 1
= 8
Therefore,
6 + 4/a + b/3 = 8 when a = 4 and b = 3
Note:
4/4 = 1
3/3 = 1
Travis and Beth went to the corner mini-mart. Travis bought 6 candy bars and 2 sodas for $4.88. Beth bought 2 candy bars and 3 sodas for $3.47. All candy bars cost the same and all sodas are the same price. Determine the price of a candy bar and the price of a soda.
Answers
Answer:
Hence candy = $0.55 and soda= $0.48
Step-by-step explanation:
Given data
Travis bought 6 candy bars and 2 sodas for $4.88
6x+2y= 4.88------------1
Beth bought 2 candy bars and 3 sodas for $3.47
2x+3y= 3.47----------2
solve 1 and 2
6x+2y= 4.88------------1x 3
2x+3y= 3.47----------2 X 2
18x+6y=14.64
- 4x+6y= 6.94
14x=7.7
divide both sides by 14
x= 7.7/14
x=$0.55
put x= 0.55 in 1
6(0.55)+2y= 4.88------------1
3.3+2y= 4.88
3.3y= 4.88-3.3
3.3y=1.58
y=1.58/3.3
y=$0.48
Number graph ranging from negative two to ten on the x and y axes. A line labeled y equals begin fraction three over two end fraction times x is drawn on the graph. A second line, labeled y equals begin fraction negative one over two end fraction x plus four, is drawn on the graph. What is the solution to the system of equations represented by these two lines? Responses (2, 0) (2, 0) (0, 4) (0, 4) (4, 2) (4, 2) (2, 3)
Answers
Answer:
Step-by-step explanation:
To find the solution to the system of equations represented by the two lines, we need to find the point where they intersect on the graph.
First, let's find the coordinates of the intersection point by solving the system of equations. We have:
y = (3/2)x (Equation 1)
y = (-1/2)x + 4 (Equation 2)
To find the intersection point, we need to set the two equations equal to each other:
(3/2)x = (-1/2)x + 4
Simplifying this equation, we get:
2x = 8
x = 4
Now that we know x = 4, we can substitute this value into either Equation 1 or Equation 2 to find the corresponding value of y:
y = (3/2)x
y = (3/2)(4)
y = 6
Therefore, the solution to the system of equations represented by the two lines is (4, 6).
what is the product of 3 square root 7 and 17 square root 14 in simplest radical form
Answers
\(3 \sqrt{7} \times 17 \sqrt{14} \)
This is the problem that we need to solve. The best way to get about it is to first:
Multiply the constant numbers (3 and 17). 3×17 is 51. Next multiply the radicals. \( \sqrt{7} \times \sqrt{14} = \sqrt{7 \times 14} = \sqrt{108} \)Simplify the squareroot of 108 since it is 49 times 2. It would be equal to 7 squareroots of 2. Our final answer would be:\(51 \times 7\sqrt{2} = 357 \sqrt{2} \)51 x 7 is 357, so the answer above is right.The skills needed are multiplication, mulitplication of radicals, and simplifying radicals, so if you want to review anything use these as reference.
Hope you understood and have a nice day!!
Use Lagrange multipliers to find the volume of the largest rectangular box in the first octant with three faces in the coordinate planes and one vertex in the given plane. x + 3y + 4z = 9_______.
Answers
The largest rectangular box in the first octant with three faces in the coordinate planes and one vertex in the plane x + 3y + 4z = 9 has dimensions x = 1.5, y = 1, and z = 2.25, with a maximum volume of 3.375 cubic units.
To find the largest rectangular box in the first octant with three faces in the coordinate planes and one vertex in the plane x + 3y + 4z = 9, we can use the method of Lagrange multipliers.
Let the sides of the rectangular box be represented by the variables x, y, and z. We want to maximize the volume V = xyz subject to the constraint x + 3y + 4z = 9.
The Lagrangian function is then given by L = xyz + λ(x + 3y + 4z - 9).
Taking the partial derivatives of L with respect to x, y, z, and λ, and setting them equal to zero, we get:
yz + λ = 0
xz + 3λ = 0
x*y + 4λ = 0
x + 3y + 4z - 9 = 0
Solving these equations simultaneously, we get:
x = 1.5, y = 1, z = 2.25, and λ = -0.5625
Therefore, the maximum volume of the rectangular box is V = 1.512.25 = 3.375 cubic units.
To learn more about coordinate planes
https://brainly.com/question/13611766
#SPJ4
Q1-) Consider a manufacturing system with two machines. Suppose that when both ma- chines are available, one is in use and the other is on standby. The probability that a machine in use fails during a day is p. When it fails its repair may start only the next day if the single repair facility is available. It takes two days to repair a failed machine. We can use a Markov Chain model to describe the evolution of this system. Let Xn = (i, j), n ≥ 0 denote the states of the Markov chain, where i is the number of machines in working condition and j is the number of elapsed repair days of a machine at the repair facility at the beginning of the n'th day. The corresponding transition probability matrix is (2,0) (1,0) (1,1) (0,1) (2,0) [1-p P 0 0 (1,0) 0 0 1-p Р P= (1,1) 1-p 0 0 P (0,1) 0 1 0 0 For parts (a)-(c) do not assume a specific value for p, leave your answer in terms of p. (a) Given Xo = (1, 1), what is the probability that only one machine is in working condition after two days? (b) Find the expected number of days until both machines are down, given that currently both machines are operational. (c) Find the steady state probabilities. (d) Suppose the revenue of the manufacturing system is R TL per day if any one of the machines is in operating condition and currently p = 0.3. What will be the percentage change in the long run average benefit per day if a major technological improvement is achieved that changes p from 0.3 to 0.2?
Answers
(a) To find the probability that only one machine is in working condition after two days, we need to determine the probability of transitioning from state (1, 1) to state (1, 0) after two days.
From the transition probability matrix, we see that to transition from (1, 1) to (1, 0) in one day, both machines need to remain operational, which has a probability of (1 - p) * (1 - p) = (1 - p)^2.
Therefore, the probability of transitioning from (1, 1) to (1, 0) after two days is ((1 - p) * (1 - p))^2 = (1 - p)^4.
(b) To find the expected number of days until both machines are down, given that currently both machines are operational, we need to consider the transition probabilities from state (2, 0) to state (0, 1).
From the transition probability matrix, we see that to transition from (2, 0) to (0, 1) in one day, both machines need to fail, which has a probability of p * p = p^2.
Therefore, the expected number of days until both machines are down, given that both machines are currently operational, is 1 / (p^2).
(c) To find the steady-state probabilities, we need to solve the equation πP = π, where π is the row vector of steady-state probabilities and P is the transition probability matrix.
Solving this equation will give us the steady-state probabilities for each state (i, j). Since the given matrix is not provided, it is not possible to calculate the exact steady-state probabilities without the specific values of the transition probabilities.
(d) To determine the percentage change in the long-run average benefit per day if p changes from 0.3 to 0.2, we would need to know how the revenue R TL is related to the probability p. Without this information, it is not possible to calculate the percentage change.
To learn more about probability : brainly.com/question/31828911
#SPJ11
Suppose you live at 29 degrees north latitude and 111 degrees west longitude. How many degrees would the North Celestial Pole appear above your horizon
Answers
The North Celestial Pole would appear 61 degrees above your horizon at 29 degrees north latitude and 111 degrees west longitude.
To calculate how many degrees the North Celestial Pole would appear above your horizon, we need to take into account your latitude. At the North Pole, the North Celestial Pole is directly overhead (90 degrees above the horizon), while at the equator, it is on the horizon (0 degrees above the horizon).
The angle between the horizon and the North Celestial Pole is equal to your latitude. Therefore, at 29 degrees north latitude, the North Celestial Pole would appear:
90 degrees - 29 degrees = 61 degrees above the horizon.
So the North Celestial Pole would appear 61 degrees above your horizon at 29 degrees north latitude and 111 degrees west longitude.
Learn more about The angle
https://brainly.com/question/28451077
#SPJ4
What is the midpoint of the line segment that connects the points located at (10,-13) and (-8,5)
Answers
Answer:
midpoint=(X1+X2),(Y1+y2)
=(10-8),(-13+5)
=(2,2)
Aurora earns a salary of $25,000 per year. Her benefits are equal in value to 30 percent of her salary. What is the value of Aurora’s benefits?
Answers
Move the decimal over one to get 10% and then multiply by 3 (30%)
write out all functions :{1,2,3,4}→{,} (using two-line notation)
Answers
There are 16 functions in total.
8 functions are surjective, meaning that every element in the codomain is the image of at least one element in the domain.
4 functions are injective, meaning that no two elements in the domain have the same image.
0 functions are bijective, meaning that they are both surjective and injective.
A function is a relation that maps each element in the domain to exactly one element in the codomain. In this case, the domain is {1, 2, 3, 4} and the codomain is {,}.
To write a function in two-line notation, we list the domain elements on the left-hand side of the arrow, and the corresponding codomain elements on the right-hand side of the arrow. For example, the function that maps 1 to , 2 to , 3 to , and 4 to is written as:
f(1) = ,
f(2) = ,
f(3) = ,
f(4) = .
There are a total of 16 possible functions, because there are 16 possible ways to assign the domain elements to the codomain elements.
The 8 surjective functions are those that map each element in the domain to a different element in the codomain. For example, the function that maps 1 to , 2 to , 3 to , and 4 to is surjective.
The 4 injective functions are those that do not map two different domain elements to the same codomain element. For example, the function that maps 1 to , 2 to , 3 to , and 4 to is injective.
There are no bijective functions, because there is no way to map the four elements in the domain to the two elements in the codomain without creating a function that is either not surjective or not injective.
Learn more about bijective function here:
brainly.com/question/30241427
#SPJ11
There are 16 functions in total.
8 functions are surjective, meaning that every element in the codomain is the image of at least one element in the domain.
4 functions are injective, meaning that no two elements in the domain have the same image.
0 functions are bijective, meaning that they are both surjective and injective.
A function is a relation that maps each element in the domain to exactly one element in the codomain. In this case, the domain is {1, 2, 3, 4} and the codomain is {,}.
To write a function in two-line notation, we list the domain elements on the left-hand side of the arrow, and the corresponding codomain elements on the right-hand side of the arrow. For example, the function that maps 1 to , 2 to , 3 to , and 4 to is written as:
f(1) = ,
f(2) = ,
f(3) = ,
f(4) = .
There are a total of 16 possible functions, because there are 16 possible ways to assign the domain elements to the codomain elements.
The 8 surjective functions are those that map each element in the domain to a different element in the codomain. For example, the function that maps 1 to , 2 to , 3 to , and 4 to is surjective.
The 4 injective functions are those that do not map two different domain elements to the same codomain element. For example, the function that maps 1 to , 2 to , 3 to , and 4 to is injective.
There are no bijective functions, because there is no way to map the four elements in the domain to the two elements in the codomain without creating a function that is either not surjective or not injective.
Learn more about bijective function here: brainly.com/question/30241427
#SPJ11
what’s is the quotient for the rational expression shown below?
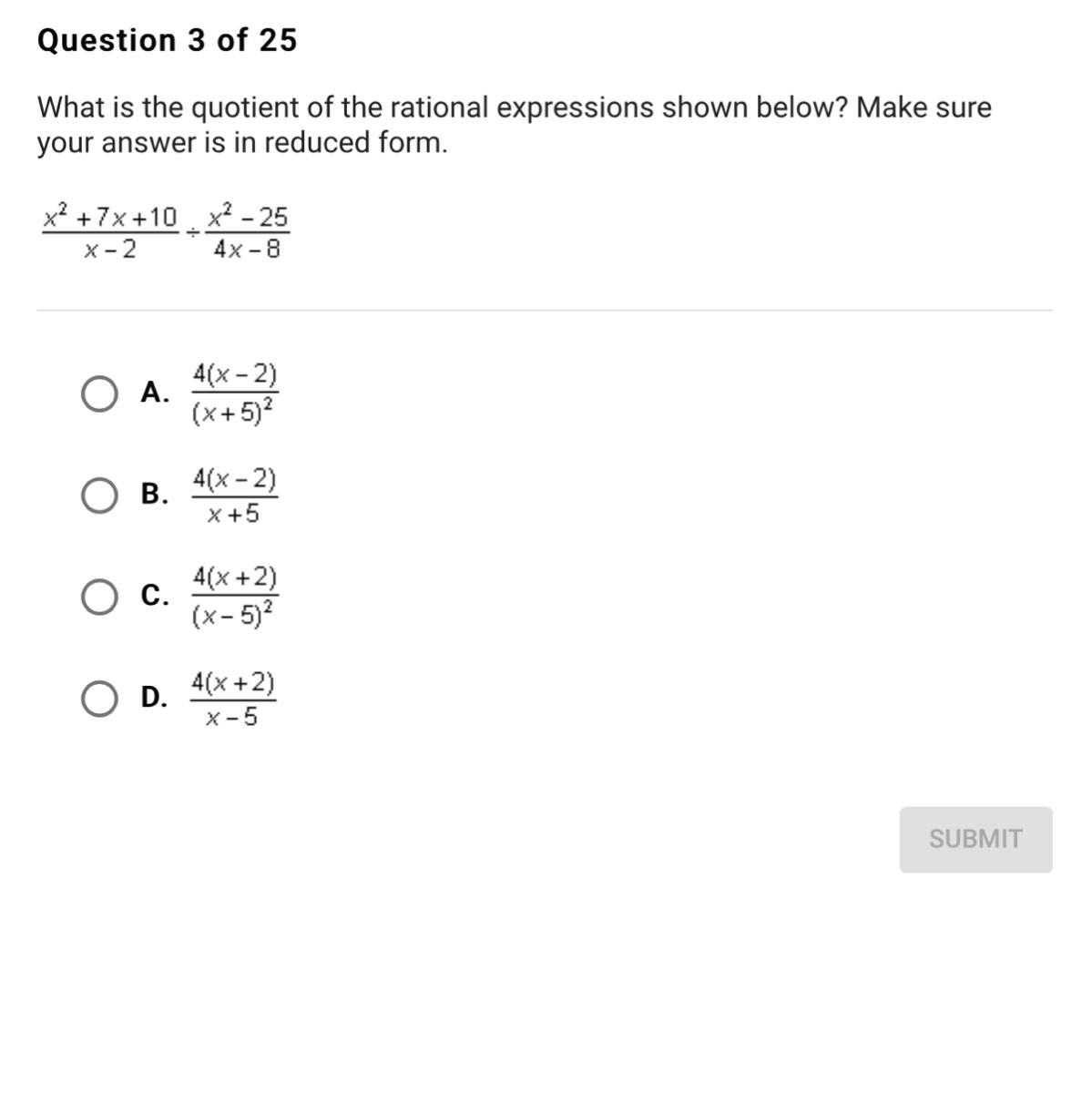
Answers
Answer:
D
Step-by-step explanation:
D is the correct answer
If afc is $8 at a quantity of output of 1,000 units, and atc is $12 at the same level of output, it follows that:_______.
Answers
The AFC represents the fixed portion of the total cost, while the difference between ATC and AFC represents the variable cost per unit.
To determine the relationship between average fixed cost (AFC) and average total cost (ATC) at a quantity of output of 1,000 units, we need to understand the formulas for AFC and ATC.
AFC is calculated by dividing total fixed cost (TFC) by the quantity of output (Q). ATC is calculated by dividing total cost (TC) by the quantity of output (Q). Mathematically, we have:
AFC = TFC / Q
ATC = TC / Q
Given that AFC is $8 at a quantity of output of 1,000 units, we can substitute the values into the AFC formula:
$8 = TFC / 1,000
Multiplying both sides of the equation by 1,000, we find:
TFC = $8,000
Now, we are given that ATC is $12 at the same level of output. Substituting the values into the ATC formula, we have:
$12 = TC / 1,000
Multiplying both sides of the equation by 1,000, we find:
TC = $12,000
To summarize:
Total fixed cost (TFC) = $8,000
Total cost (TC) = $12,000
Therefore, it follows that the difference between AFC and ATC lies in the variable cost component. The AFC represents the fixed portion of the total cost, while the difference between ATC and AFC represents the variable cost per unit.
Learn more about average fixed cost here:
https://brainly.com/question/13541145
#SPJ11
Electricty what is the voltage V of an electron circuit with a current C of 2-j and an impedence i of 3+2j? Use the formula v=ci
Answers
The value of the voltage of the electricity is 6 + j + 2j²
How to determine the voltage of the electricity?From the question, we have the following parameters that can be used in our computation:
C = 2 - j
I = 3 + 2j
The formula of voltage is given as
V = CI
Substitute the known values in the above equation, so, we have the following representation
V = (2 - j) * (3 + 2j)
Open the brackets
So, we have
V = 6 + 4j - 3j + 2j²
Evaluate the like terms
V = 6 + j + 2j²
Hence, the voltage is 6 + j + 2j²
Read more about voltage at
https://brainly.com/question/14883923
#SPJ1
Evaluate the logarithmic function for the given value.
f(x) = log5 x for f(125)
f(125)=(
HELP!

Answers
Answer:
\(f(125) = log_{5}(125 ) \\ = log_{5}( {5}^{3} ) = 3 log_{5}(5 ) = 3(1) = 3\)
Given:
b (x) = x2+7x
Find
B(7)
Answers
Answer:
Step-by-step explanation:
b(7) = 7^2 + 7(7)
B(7) = 49 + 49
B(7) = 98
Previous Answers Set up, but do not evaluate, an integral for the volume of the solid obtained by rotating the region in the first quadrant bounded by the curves y-tan-x, y-3, and x-0 about the line y-3. tan(2x)2x dx 0
Answers
To set up an integral for the volume of the solid obtained by rotating the region in the first quadrant bounded by the curves y = tan(x), y = 3, and x = 0 about the line y = 3, we use the formula V = π∫a b[(R(x))^2 - (r(x))^2]dx, where R(x) and r(x) are the radius of the outer and inner circle respectively.
For this problem, a = 0 and b = 2 since the region is in the first quadrant. We can calculate the radii of the inner and outer circle by substituting in the boundaries of the region:
R(x) = 3 - tan(x)
r(x) = 3 - 3 = 0
So, the integral to calculate the volume of the solid obtained by rotating the region in the first quadrant bounded by the curves y = tan(x), y = 3, and x = 0 about the line y = 3 is:
V = π∫02[(3 - tan(x))^2 - 0]dx
for more volume questions ,refer here:
https://brainly.com/question/30550584#
#SPJ11
Solve for
1. f(6)
2. g(-3)
3. f(2)+g(2)
4. f(4)-g(4)
Answers
Answer:
call me nap is hi answer is f2+g2
2. -3g
3. 2(f+g)
4. 4(f+g)
I need a genuine answer. Don't answer if you don't know. Need a proper explanation.

Answers
Answer:
Step-by-step explanation:
If m and n are both 1 then
Minimum value = 10^(1+1) * 3^(1-1) * 225
= 325.
If m and n have to be different, then m = 2 and n = 1
Minimum value = 10^3 * 3^1 * 15^2
= 675,000.
If m >= n then N will also be natural which is a subset of rational numbers.
If m < n then 3^(m - n) will be less than 1 and N will need to be written as a fraction, which are still rational.
The minimum values for both m and n are 1 by definition.