1) The rational function shown could be used to the number of arrests, f(x), per 100,000 drivers, for driving under the influence of alcohol, as a function of a driver’s age, x.
\(f(x)=\frac{27725(x-14)}{x^2+9} -5x\)
a) Describe the trend you see in the graph, in context.
b)Use a graphing utility to determine the age that corresponds to the greatest number of arrests.
Answers
The age that has the maximum number of arrest is 25 years
The trend on the graphThe equation of the function is given as:
\(f\left(x\right)\ =\ \frac{27725\left(x\ -\ 14\right)}{x^{2\ }+\ 9}-5x\)
See attachment for the graph of the function.
The end behavior of the graph is
\(\mathrm{as}\:x\to \:+\infty \:,\:f\left(x\right)\to \:-\infty \:,\:\:\mathrm{and\:as}\:x\to \:-\infty \:,\:f\left(x\right)\to \:+\infty \:\)
This means that:
As the age of the driver increases, arrested drivers decreases and as the age of the driver decreases, arrested drivers increases
The age that has the maximum arrest
From the graph, the maximum is:
Maximum = (25.388, 356.166)
Remove the y values
Maximum = 25.388
Approximate
Maximum = 25
Hence, the age that has the maximum arrest is 25
Read more about functions at:
https://brainly.com/question/23426439
#SPJ1

Related Questions
In ΔQRS, the measure of ∠S=90°, SR = 45, QS = 28, and RQ = 53. What is the value of the tangent of ∠Q to the nearest hundredth?
Answers
Answer:
Aprox: 1.61
Step-by-step explanation:
TOA: Tan Q = Opposite/Adjacent = 45/28 ---> 1.61
Answer:
28/45≈1.6071≈1.61
Step-by-step explanation:
please help i will give 20 points if added demonstration on how to graph the answer

Answers
Your equation
-4y = -6x + 8
Change to y intercept form y=mx+b
-4y = -6x + 8
Divide all parts by -4
-4/-4 y = -6/-4 x + 8/-4
Simplify
y = 3/2x - 2
Now graph
Start with y intercept (b) = -2
Mark your coordinate -2 on the y axis
Now from your -2 point, plot your next point using your slope of 3/2 (which is y/x) by going up +3 and right +2 and plot your point. Do this again for three points on your graph and draw your line.
Your coordinates are
(0, -2)
(2, 1)
(4, 4)

The solution is the factor 4y - 6x:. 2(2y - 3x) = 2(2y - 3x). 8 = 2• 4 =. 2(2y - 3x)
8. 2• 4
cancel the common factor: 2
= 2y - 3x. the answer is 2y - 3x
4 4
I NEED HELP! I AM THE WORST AT MATH
Jonah is playing a video racing game called Checkpoint. The speed of Jonah’s car is recorded four times during one lap. At the first checkpoint, his speed is 80 miles per hour. At the second checkpoint, his speed has reduced by 5%. At the third checkpoint, Jonah’s speed has increased by the speed from the previous checkpoint. At the fourth checkpoint, his speed decreased by 20% compared with the third checkpoint. What is Jonah’s net change in speed between the first and fourth checkpoints?
A. 4
B. -4
C. 15
D. -15
Answers
Answer:
Its -15 or D
Step-by-step explanation:
Answer:
D. -15
Step-by-step explanation:
Which of the following best describes ethics?
it is a set of thoughts that are made about kinds of individuals
or their manners of conducting activities
it is a set of values that define r
Answers
Answer:
the second
Step-by-step explanation:
refers to well-founded standards of right and wrong that prescribe what humans should do, usually in terms of rights, obligations, benefits to society, justice
Question A cylindrical swimming pool has a diameter of 18 feet and a height of 5.5 feet. How many gallons of water can the pool contain? Round your answer to the nearest whole number. (1 ft3 ≈ 7.5 gal)
Answers
The pool can contain 10492 gallons of water
What is volume of cylinder?
The capacity of a cylinder, which determines how much material it can carry, is determined by the cylinder's volume. There is a formula for the volume of a cylinder that is used in geometry to determine how much of any quantity, whether liquid or solid, may be immersed in it uniformly. A cylinder is a three-dimensional structure having two parallel, identical bases that are congruent.
Right circular cylinder: A cylinder with circular bases and a lateral curved surface with each line segment perpendicular to the bases.
Oblique Cylinder: A cylinder with sides that are inclined over the base at a different angle than a right angle.
An elliptic cylinder is a cylinder with ellipses at its bases.
Two right circular cylinders tied together inside of one another form a right circular hollow cylinder.
volume of cylinder= (π)\(r^2h\)
diameter= 18feet
radius = 9 feet
height = 5.5 feet
volume= 3.14*(\(9^2\))*5.5
= 1398.87 \(feet^3\)
volume in gallons = 1398.87 * 7.5
= 10492 gallons
Learn more about volume of cylinder from the link below
https://brainly.com/question/16134180
#SPJ1
A group contains n men and n women. How many ways are there to arrange these people in a row if the men and women alternate? Justify.
Answers
So, there are (n!)^2 ways to arrange n men and n women in a row if they alternate genders.
We need to use the principle of multiplication. We first choose the position of the first person in the row, which can be any of the n men or n women. Without loss of generality, let's say we choose a man. Then, for the next position, we need to choose a woman since we are alternating genders. There are n women to choose from. For the third position, we need to choose another man, and there are n-1 men left to choose from (since we already used one). For the fourth position, we need to choose another woman, and there are n-1 women left to choose from. We continue this pattern until all n men and n women are placed in the row.
Using the principle of multiplication, we can find the total number of ways to arrange the people by multiplying the number of choices at each step. Therefore, the total number of ways to arrange the people in a row if the men and women alternate is:
n * n-1 * n * n-1 * ... * 2 * 1
This can be simplified to:
(n!)^2
So, there are (n!)^2 ways to arrange n men and n women in a row if they alternate genders.
To know more about alternate visit:
https://brainly.com/question/13169213
#SPJ11
for geometry:(
i’ll give a brainist!!!

Answers
Answer: Angle T is 45
Step-by-step explanation:

2(10+10x)=60
Anyone willing to help?
Answers
2(10+10x)=60
20+20x=60
-20 -20
20x=40
x=2
2x10x=20x
20+20x=60
-20. -20
———————-
20x=40
—- ——
20. 20
X=2
g(x) = 2 log(x - 1)
what is the inverse
Answers
Answer:
\(g^{-1}(x)=1+10^{x/2}\)
Step-by-step explanation:
Inverse Function
Let's call:
\(y=2 log(x-1)\)
Divide by 2:
\(y/2=log(x-1)\)
Assuming the base of the log is 10, apply exponential base 10:
\(10^{y/2}=x-1\)
Solving for x:
\(x=1+10^{y/2}\)
Swap variables:
\(y=1+10^{x/2}\)
Calling this function the inverse:
\(\boxed{g^{-1}(x)=1+10^{x/2}}\)
registrants at a large convention are offered 6 sightseeing tours on each of 3 days. in how many ways can a person arrange to go on a sightseeing tour planned by this convention?
Answers
The registrants would be able to see the 6 sightseeing tours in 18 ways.
Here it is given that the convention has organized the 6 sightseeing tours on 3 days each.
This implies that the 6 sightseeing tours are available on all three days.
Hence, the registrants would be able to book the tour on any of the one days.
Hence, on day 1
the registrants will be able to tour in ways
On day 2
the registrants would again be able to tour in 6 ways,
Similarly on day 3, they will again be able to tour in 6 ways.
Since they need to choose either of the days given, the total number of ways to tour will be
no.of ways for day 1 + no. of ways for day 2 + no. of d6ays for day 3
= 6 + 6 + 6
= 18 ways
Hence, they can go on a sightseeing tour in 18 ways.
To learn more about combinations visit
https://brainly.com/question/28047704
#SPJ4
Use the Chain Rule to find the indicated partial derivatives. z=x3+xy2,x=uv3+w2,y=u+vew ∂u∂z,∂v∂z,∂w∂z when u=2,v=1,w=0 ∂u∂z= ∂v∂z= ∂w∂z= Show My Work (Required) (3) What steps or reasoning did you use? Your work counts towards your score. You can submit show my work an unlimited number of times.
Answers
when u = 2,v = 1, and w = 0, the partial derivatives are
∂u/∂z = 0,
∂v/∂z = 0, and
∂w/∂z = 0.
To find the partial derivatives ∂u/∂z, ∂v/∂z, and ∂w/∂z using the Chain Rule, we follow these steps:
Calculate ∂u/∂z:
∂u/∂x = 0 (since u is a constant)
∂u/∂y = 0 (since u is a constant)
∂x/∂z = y² (using the given expression for z)
∂y/∂z = 0 (since y is not directly dependent on z)
Plugging these values into the formula:
∂u/∂z = (∂u/∂x) * (∂x/∂z) + (∂u/∂y) * (∂y/∂z)
= 0 * y² + 0 * 0
= 0.
Calculate ∂v/∂z:
∂v/∂x = 0 (since v is a constant)
∂v/∂y = 0 (since v is a constant)
∂x/∂z = y² (using the given expression for z)
∂y/∂z = 0 (since y is not directly dependent on z)
Plugging these values into the formula:
∂v/∂z = (∂v/∂x) * (∂x/∂z) + (∂v/∂y) * (∂y/∂z)
= 0 * y² + 0 * 0
= 0.
Calculate ∂w/∂z:
∂w/∂x = 0 (since w is a constant)
∂w/∂y = 0 (since w is a constant)
∂x/∂z = y² (using the given expression for z)
∂y/∂z = 0 (since y is not directly dependent on z)
Plugging these values into the formula:
∂w/∂z = (∂w/∂x) * (∂x/∂z) + (∂w/∂y) * (∂y/∂z)
= 0 * y² + 0 * 0
= 0.
Therefore, When u = 2, v = 1, and w = 0, the partial derivatives ∂u/∂z,
∂v/∂z, and ∂w/∂z are all equal to 0.
To know more about partial derivatives, visit:
https://brainly.com/question/30967637
#SPJ11
What is angle 2? I don’t know this please help me
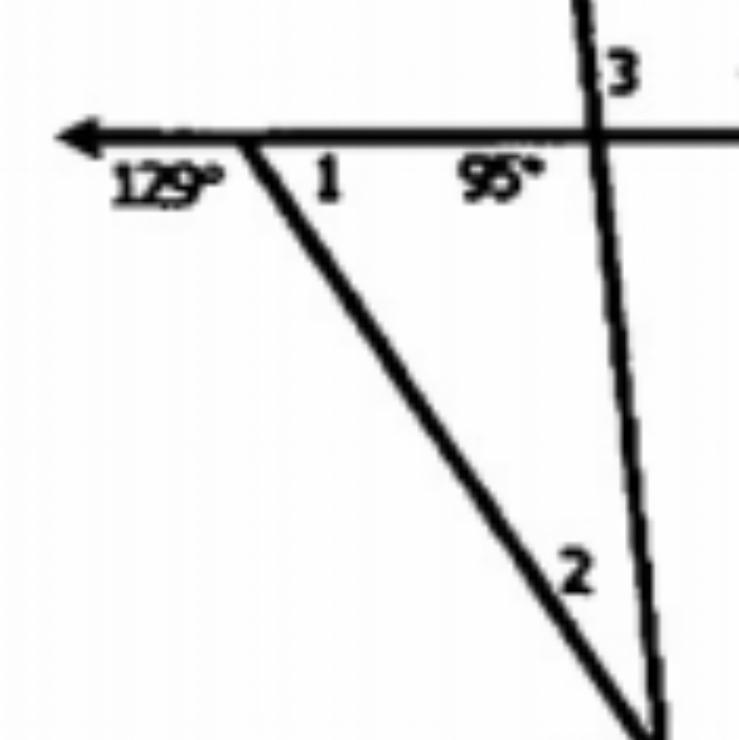
Answers
Answer:
Acute angle
Step-by-step explanation:
Since it's measure is less than 90 degrees
if the product of two consecutive even number is 224 find the number
Answers
Answer:
Let one integer be x, and the other be (x+2)
x(x+2)=224
x2+2x-224=0
(x+16)(x-14) =0
x=-16 or 14
so x+2 = -14 or 16
So the integers are either 14 and 16 or -14 and -16.
Step-by-step explanation:
was that the question?
Let the first consecutive even number be x. The second one is going to be two more than x, and as such can be written as (x+2).
The product of these numbers, x and (x+2), is 224:
x(x+2)=224
x²+2x=224
x²+2x-224=0
(x+16)(x-14) =0 (could also use '-b' method)
x=-16 or 14
Therefore, (x+2) = -14 or 16
Therefore, the numbers are either 14 and 16, or -14 and -16
if a regulation basketball is randomly selected, what is the probability that it will weigh between 20.5 and 23.5 ounces?
Answers
Therefore, the probability that basketball will weigh between 20.5 and 23.5 is 0.866
What is probability ?Probability is the concept that describes the likelihood of an event occurring. In real life, we frequently have to make predictions about how things will turn out. We may be aware of the result of an occurrence or not. When this is the case, we refer to the likelihood that the event will occur or not.
Here,
X υ N (22,1)
Probability that basketball will weigh between 20.5 and 23.5
is:
=> P(20.5 < x < 23.5)= P[ 20.5-22/1 < z < 23.5-22/ 1 ]
=> P(20.5 < x < 23.5) = P(-1.5 < z < 1.5)
=> P(20.5 < x < 23.5) = 0.866
Therefore, the probability that basketball will weigh between 20.5 and 23.5 is 0.866
To know more about probability , visit
https://brainly.com/question/11234923
#SPJ4
Solve x to the nearest tenth

Answers
The value of x is 4.47 units
In the given figure, there are two right angle triangle, to find the value of x we have to solve each triangle using the Pythagorean theorem.
Consider the bottom triangle
Base of the triangle = 6 units
The hypotenuse of the triangle = 9 units
Apply the Pythagorean theorem
The third side of the triangle = \(\sqrt{9^2-6^2}\)
= \(\sqrt{81-36}\)
= \(\sqrt{45}\) units
Similarly consider the top triangle
The base of the triangle = 5 units
The hypotenuse of the triangle = \(\sqrt{45}\) units
The third side of the triangle = \(\sqrt{\sqrt{45}^2- 5^2}\)
= \(\sqrt{45-25}\)
= \(\sqrt{20}\)
= 4.47 units
Hence, the value of x is 4.47 units
Learn more about Pythagorean theorem here
brainly.com/question/14930619
#SPJ1
The function below represents the position f in feet of a particle at time x in seconds. find the average height of the particle on the given interval
f(x) = 3x^2 + 6x, [-1, 5]
Answers
Therefore, the average height of the particle on the interval [-1, 5] is approximately 33.67 feet.
To find the average height of the particle on the interval [-1, 5], we need to evaluate the definite integral of the position function f(x) = 3x^2 + 6x over that interval and divide it by the length of the interval.
The average height (H_avg) is calculated as follows:
H_avg = (1 / (b - a)) * ∫[a to b] f(x) dx
In this case, a = -1 and b = 5, so the average height is:
H_avg = (1 / (5 - (-1))) * ∫[-1 to 5] (3x^2 + 6x) dx
To evaluate the integral, we can use the power rule of integration:
∫ x^n dx = (1 / (n + 1)) * x^(n+1) + C
Applying this rule to each term in the integrand, we get:
H_avg = (1 / 6) * [x^3 + 3x^2] evaluated from -1 to 5
Now, we can substitute the limits of integration into the expression:
H_avg = (1 / 6) * [(5^3 + 3(5^2)) - ((-1)^3 + 3((-1)^2))]
H_avg = (1 / 6) * [(125 + 75) - (-1 + 3)]
H_avg = (1 / 6) * [200 - (-2)]
H_avg = (1 / 6) * 202
H_avg = 33.67 feet
To know more about interval,
https://brainly.com/question/1619430
#SPJ11
Can someone help me with this math homework please!

Answers
Answer:
Table 2.
Step-by-step explanation:
Recall that by definition, a linear function increases linearly. That is, the rate of change between any two points is constant.
We can go through each table and verify its rate of change.
Table 1)
For Table 1, note that y = -19 when x = 0.
When x = 1, y = -11. In other words, we added 8 for every increase of one for x.
When x = 2, y = -3. We still increased by 8 for every increase of one for x.
When x = 3, y = 5. Since -3 + 8 = 5, all points in Table 1 shows a constant rate of change.
In conclusion, Table 1 represents a linear function.
Table 2)
For Table 2, note that y = -1.5 when x = 0.
When x = 1, y = -1.5. In other words, we increased by 3 for every increase of one for x.
However, when x = 2, y = 3. This time, we only increased by 1.5 for every increase of one for x. Since the two rates are not equivalent, Table 2 is nonlinear.
Table 3)
Again, note that for Table 3, y = 15 when x = 0.
When x = 1, y = 12. So, we decreased by 3 for every increase of one for x.
When x = 2, y = 9. And when x = 3, y = 6. For both cases, we still decreased by 3 for every increase of one for x.
In conclusion, Table 3 represents a linear function.
Therefore, the table that represents a nonlinear function is Table 2.
i will love you forever if you help me I am failing and this is like my only hope and i have no clue how to do this so thank you sm you smart person

Answers
Answer:
Step-by-step explanation:
product of (2.5 x 10²) x (10⁵)=2.5 x 10⁷
when we multiply the powers we add the 2+5=7
Answer:
9.25×10^7
Step-by-step explanation:
2.5 × 3.7 =9.25 and 10^2+10^5=10^7
How many degrees are in a semicircle? 36° 90° 270° 180°
Answers
Answer:
180°
Step-by-step explanation:
The baseball game started at 7:05 it ended at 9:15 how long was the baseball game
Answers
The baseball game lasted 2 hours and 10 minutes.
To calculate how long the baseball game lasted, we must begin by taking the start time of 7:05. We can convert this time to a numerical value by adding 7 hours and 5 minutes, which equals 705 minutes. Next, we must do the same with the end time of 9:15. Adding 9 hours and 15 minutes gives us a total of 915 minutes. Subtracting the start time from the end time gives us a difference of 210 minutes. Finally, we must convert the minutes back to hours and minutes, which gives us 2 hours and 10 minutes. Therefore, the baseball game lasted 2 hours and 10 minutes.
Learn more about minutes here
https://brainly.com/question/13624026
#SPJ4
what is 2x3x4x2x88x9x112x100x9x2?
;)
Answers
Answer:
7664025600
Step-by-step explanation:
I basically just multiplied first then added the sums. Also you can use a calculator to make sure ur answer is right.
g(x) = 9(2x2 + 6
)
Determine g(1)
Answers
Answer:
g(1) = 72
General Formulas and Concepts:
Pre-Alg
Order of Operations: BPEMDASStep-by-step explanation:
Step 1: Define
g(x) = 9(2x² + 6)
g(1) is x = 1
Step 2: Solve
Substitute: g(1) = 9(2(1)² + 6)Evaluate: g(1) = 9(2(1) + 6)Multiply: g(1) = 9(2 + 6)Add: g(1) = 9(8)Multiply: g(1) = 72Given the directrix of y = 6 and focus of (0, 4), which is the equation of the parabola?
y = −one fourthx2 + 5
y = −one fourthx2 − 5
y = one fourthx2 + 5
y = one fourthx2 − 5
Answers
Answer:
a) The equation of the parabola
\(y = \frac{-x^{2} }{4} +5\)
Step-by-step explanation:
Explanation:-
Step(i):-
Given the directrix of the parabola y = 6
Focus of the parabola S(0,4)
The standard equation of the parabola
( x- h)² = 4 a (y-k)
(h,k) is the vertex of the parabola
Axis of the parabola is parallel to y-axis
Given the directrix of the parabola y = 6
The directrix of the parabola y = k -a = 6
k-a =6 ...(i)
The focus of the parabola
S( h , K+a) = (0,4)
so h = 0 and K+a =4
K+a =4 ....(ii)
Step(ii):-
Solving (i) and (ii) equations , we get
Adding (i) and (ii) equations and we get
K-a + k+a = 6 +4
2 K = 10
K =5
Substitute K =5 in equation (i)
K -a =6
5 -a =6
5-6 =a
a = -1
Step(iii):-
we have (h,k) =( 0,5) and a = -1
The equation of the parabola
( x- h)² = 4 a (y-k)
( x- 0)² = 4 (-1) (y-5)
x² = -4 y + 20
-4 y = x² - 20
dividing '-4' on both sides, we get
\(y = \frac{x^{2} }{-4} +\frac{-20}{-4}\)
\(y = \frac{-x^{2} }{4} +5\)
Final answer:-
The equation of the parabola
\(y = \frac{-x^{2} }{4} +5\)
Surveys get more accurate with larger sample sizes. You want an accurate survey, but your cost per respondent is $3
and your budget is $1,000. How many respondents can you survey?
ОООО
a) 333
b) 353
c) 533
d) 575
Answers
under random sampling from an infinite population, the mean of the sampling distribution of the sample mean is always equal to the mean of the underlying population. T/F
Answers
The given statement "Under random sampling from an infinite population, the mean of the sampling distribution of the sample mean is always equal to the mean of the underlying population" is TRUE.
The reason for this is that the central limit theorem (CLT) applies to large enough random samples from any population with a finite variance. According to CLT, the sampling distribution of the mean becomes approximately normal, and its mean is equal to the mean of the population.
Since the statement specifies an infinite population, it is not technically possible to obtain a sample size large enough to meet the requirements of CLT.
However, the statement remains true in theory because an infinite population with a finite variance can be thought of as a limit of a sequence of finite populations, each of which does meet the requirements of CLT.
Therefore, even though it is not practically possible to obtain a truly random sample from an infinite population, the statement remains true in theory.
For more questions like Sample mean click the link below:
https://brainly.com/question/31101410
#SPJ11
16) The angles of a quadrilateral are in AP, whose common difference is 10°.
Find all of its four angles.
Answers
Answer:
75°, 85°, 95°, 105°
Step-by-step explanation:
Since the 4 angles form an AP, then the 4 angles are
a, a + d, a + 2d, a + 3d
where a is the first term and d the common difference
The sum of the angles in a quadrilateral = 360° thus
a + a + d + a + 2d + a + 3d = 360, that is
4a + 6d = 360, substitute d = 10
4a + 60 = 360 ( subtract 60 from both sides )
4a = 300 ( divide both sides by 4 )
a = 75
Thus the 4 angles are
75°, 75° + 10° = 85°, 75° + 20 = 95°, 75° + 30° = 105°
What is the quotient when (-12x^9 + 3x^7 + 24x^6) is divided by 6x?
Answers
Answer:
(-12x^9+3x^7+24x^6)÷6=-2×^10+1/2x^8+4x^7
I need help with 32 x 134partial product
Answers
32 x 134
Partial product: Multiply each digit of 32 by each digit of 134, maintain each digit place.
(30x100) + (30x 30) + (30 x4)+ (2 x 100) + (2x30) + (2 x 4)
3,000 + 900+120+200+60+8 = 4,288
PLEASE HELP WITH MY MATH HOMEWORK
ill give brainliest

Answers
Answer:
The answer is that the ball was in the air for 0.56 seconds when it was 54 feet above the ground. This was determined by using the Quadratic Formula to solve the equation 54 = -16s^2 + 96s for the variable s.
Step-by-step explanation:
To solve this equation, we can use the Quadratic Formula, which states that for a quadratic equation in the form ax^2 + bx + c = 0, the solutions are given by:
x = (-b +/- sqrt(b^2 - 4ac)) / (2a)
In this case, a = -16, b = 96, and c = -54. Plugging these values into the Quadratic Formula, we get:
s = (-96 +/- sqrt(96^2 - 4 * -16 * -54)) / (2 * -16)
= (96 +/- sqrt(9216 + 4352)) / -32
= (96 +/- sqrt(13,568)) / -32
Since we want the time (in seconds) that the ball was in the air, we need to find the positive solution to this equation. Thus, we have:
s = (96 + sqrt(13,568)) / -32
= (96 + 120) / -32
= 0.5625 seconds
Rounding this value to the nearest hundredth of a second, we get 0.56 seconds. This means that the ball was in the air for 0.56 seconds when it was 54 feet above the ground.
To solve this equation, we used the Quadratic Formula. This method allowed us to find the time (in seconds) that the ball was in the air by solving for the value of the variable s in the given equation. This helped Vue answer his question by providing a numerical value for the amount of time that the ball was in the air when it was 54 feet above the ground.
1. x² - 1 + y(y - 2x)
somebody plz help meeeeeeeeeeeeeeeeeeeeeee
Answers
Step1:Multiply each term in the parentheses by y.
Step2: calculate the product

Answer:
\( {(x + y)}^{2} - 1\)
Step-by-step explanation:
\( {x}^{2} + y(y - 2x) - 1\)
\( {x}^{2} + {y}^{2} - 2xy - 1\)
Using the identity (a - b)^2 here ,
\( {(x + y)}^{2} - 1\)